Limiti da problemi sul triangolo isoscele

Verso l’Esame di Stato nel Liceo Scientifico
Limiti da problemi sul triangolo isoscele
(triangolo rettangolo isoscele)
Problema
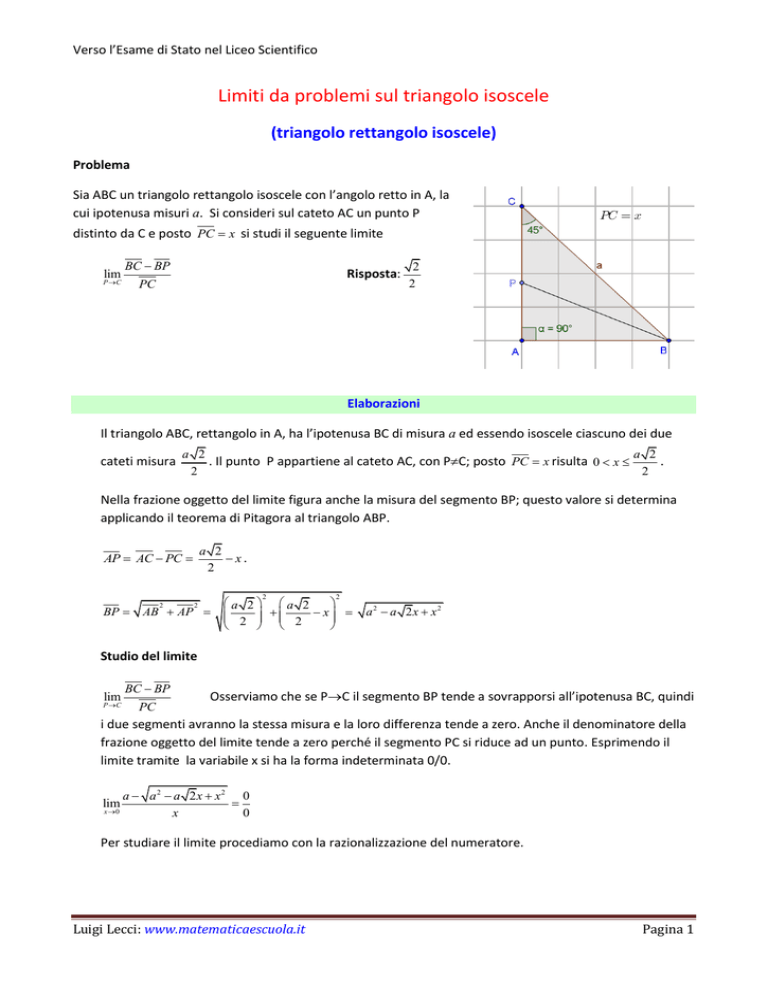
Sia ABC un triangolo rettangolo isoscele con l’angolo retto in A, la
cui ipotenusa misuri a. Si consideri sul cateto AC un punto P
distinto da C e posto PC  x si studi il seguente limite
lim
P C
BC  BP
PC
Risposta:
2
2
Elaborazioni
Il triangolo ABC, rettangolo in A, ha l’ipotenusa BC di misura a ed essendo isoscele ciascuno dei due
cateti misura
a 2
a 2
. Il punto P appartiene al cateto AC, con PC; posto PC  x risulta 0  x 
.
2
2
Nella frazione oggetto del limite figura anche la misura del segmento BP; questo valore si determina
applicando il teorema di Pitagora al triangolo ABP.
a 2
x.
2
AP  AC  PC 
2
BP 
2
2
AB  AP 
2
a 2 a 2

 x  

  
 2   2

a2  a 2x  x2
Studio del limite
lim
P C
BC  BP
PC
Osserviamo che se PC il segmento BP tende a sovrapporsi all’ipotenusa BC, quindi
i due segmenti avranno la stessa misura e la loro differenza tende a zero. Anche il denominatore della
frazione oggetto del limite tende a zero perché il segmento PC si riduce ad un punto. Esprimendo il
limite tramite la variabile x si ha la forma indeterminata 0/0.
a  a2  a 2x  x2 0

x 0
x
0
lim
Per studiare il limite procediamo con la razionalizzazione del numeratore.
Luigi Lecci: www.matematicaescuola.it
Pagina 1
Verso l’Esame di Stato nel Liceo Scientifico
a  a  a 2x  x a  a  a 2x  x

 lim
x 0
x
a  a2  a 2x  x2
2
lim
x 0

2

2
2
a2 

a2  a 2x  x2
x
  lim
2
x 0
1
a  a  a 2x  x2

2
x a 2x
1
1
a 2
2
 lim a 2  x 
 lim


x

0
x

0
2a
2a
2a
2
x

Luigi Lecci: www.matematicaescuola.it

Pagina 2