NONA LEZIONE – GALLERIA DI ISOMETRIE
Ci sono quattro tipi di isometrie elementari:
•
•
•
•
traslazioni
riflessioni
rotazioni
glisso-riflessioni
Le definizioni di traslazione, riflessione e rotazione sono elementari:
•
Nella traslazione ogni punto subisce lo stesso spostamento AI=A+
•
•
Nella riflessione ogni punto è mandato nel suo simmetrico rispetto ad un asse l
Nella rotazione ogni punto descrive un arco di circonferenza centrato in un punto fisso O, detto
centro della rotazione ; l’angolo al centro sotteso dall’arco è uguale per tutti i punti: esso è detto
angolo della rotazione
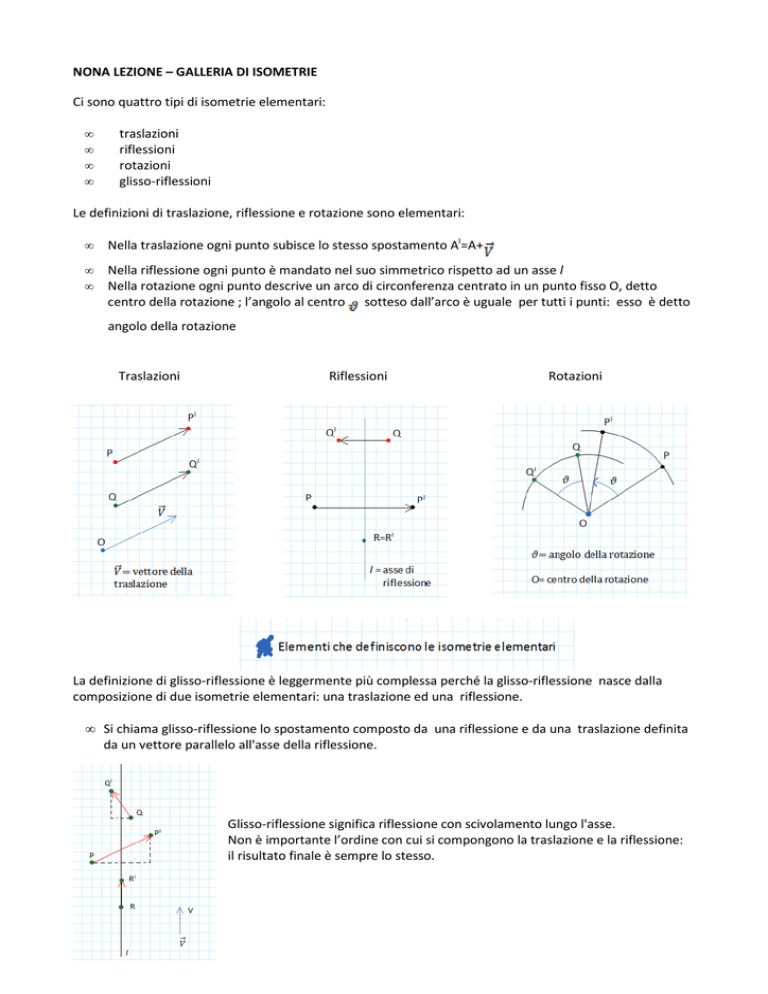
Traslazioni
Riflessioni
Rotazioni
La definizione di glisso-riflessione è leggermente più complessa perché la glisso-riflessione nasce dalla
composizione di due isometrie elementari: una traslazione ed una riflessione.
• Si chiama glisso-riflessione lo spostamento composto da una riflessione e da una traslazione definita
da un vettore parallelo all'asse della riflessione.
Glisso-riflessione significa riflessione con scivolamento lungo l'asse.
Non è importante l’ordine con cui si compongono la traslazione e la riflessione:
il risultato finale è sempre lo stesso.
Mettiamo in evidenza alcune caratteristiche importanti delle isometrie elementari.
• Isometrie e punti fissi:
Possiamo notare che le rotazioni e le riflessioni posseggono punti fissi, cioè punti che non subiscono
alcun spostamento. Le rotazioni hanno un solo punto fisso, il centro della rotazione; le riflessioni ne
hanno infiniti: tutti i punti dell’ asse della riflessione rimangono fissi. Si dice che l’ asse della riflessione è
un asse fisso.
Le traslazioni e le glisso-riflessioni non lasciano invece alcun punto fisso. L’asse della glisso-riflessione
gode della proprietà che i suoi punti scorrono lungo l’asse stesso, cosicchè l’asse non si sposta. Si dice
che l’asse della glisso-riflessione è un asse unito. Nelle traslazioni non c’è alcun asse che rimane fisso.
Rimane invariata però la direzione delle rette: una qualsiasi retta è mandata in una retta parallela.
• Isometrie e orientazione dei triangoli:
Ad ogni triangolo si può assegnare una orientazione semplicemente decidendo un verso di percorrenza
del suo perimetro. Scegliamo un ordine dei vertici, ad esempio l’ordine (A, B, C ) e conveniamo di
percorrere il perimetro del triangolo nel verso che va da A a B e quindi a C. Questo verso può essere
orario o antiorario. In questo modo distinguiamo i triangoli del piano in due categorie: quelli che sono
orientati in senso orario e quelli che sono orientati in senso antiorario.
La proprietà che vogliamo ora mettere in evidenza è che le traslazioni e le rotazioni preservano l’
orientazione dei triangoli, mentre le riflessioni e le glisso-riflessioni la cambiano. Ciò significa che
ruotando o traslando un triangolo con orientazione oraria si ottiene ancora un triangolo con
orientazione oraria ( e lo stesso vale per i triangoli con orientazione antiorario); in una riflessione il
triangolo riflesso ha invece orientazione opposta all’orientazione del triangolo originale. Quindi
operando una riflessione o una glisso-riflessione si trasforma un triangolo con orientazione oraria in un
triangolo con orientazione antioraria (e viceversa).
Si dice che le rotazioni e le traslazioni sono isometrie dirette e che le riflessioni e le glisso-riflessioni sono
isometrie inverse. Queste proprietà sono rese evidenti dalle figure che seguono:
La traslazione mantiene l’orientazione.
La riflessione inverte l’orientazione
La rotazione mantiene l’orientazione.
La glisso-riflessione (in quanto contiene una riflessione) inverte l’orientazione
Abbiamo così la seguente tavola di classificazione delle isometrie elementari:
Ha punti
fissi
Mantiene l'orientamento dei
triangoli
traslazione
NO
SI
rotazione
SI
SI
riflessione
Asse fisso
NO
glisso-riflessione
Asse unito
NO
ISOMETRIE DIRETTE
ISOMETRIE INVERSE
Punto 4: composizione di isometrie elementari
Comporre due isometrie significa eseguire le due isometrie l'una dopo l'altra nell'ordine prestabilito
(l'ordine è importante in quanto influenza il risultato finale).
Poiché ogni spostamento componente non altera le distanze, anche la trasformazione composta non altera
le distanze e quindi il risultato della composizione di isometrie è ancora un'isometria.
Si dice per questo che le isometrie formano un gruppo (chiusura rispetto alla composizione).
Proviamo a comporre due isometrie elementari. Il risultato è sorprendente: componendo, in un qualsiasi
modo, un numero arbitrario di traslazioni, rotazioni, riflessioni e glisso-riflessioni si ottiene sempre alla
fine, o una traslazione o una riflessione o una rotazione o una glisso-riflessione. Non è cioè possibile
costruire nuove isometrie componendo due isometrie elementari.
Cominciamo a verificare questa proprietà in alcuni casi particolari. Partiamo dalla composizione di due
riflessioni di assi l e m.
Bisogna distinguere il caso in cui gli assi sono paralleli dal caso in cui gli assi si intersecano in un punto O.
Caso 1: assi paralleli
Consideriamo per semplicità il caso di due assi orizzontali posti ad una distanza di quattro quadretti.
La figura mostra che, eseguendo la riflessione prima rispetto ad l e poi ad m, i punti P, Q ed R si spostano
tutti verticalmente, verso l'alto, di otto quadretti.
Risultato: la composizione di due riflessioni rispetto ad
assi paralleli l e m (nell'ordine prima l e poi m) è una
traslazione nella direzione perpendicolare agli assi, nel
verso da l a m, di un segmento pari al doppio della
distanza tra gli assi.
Caso 2: assi concorrenti in O
In ciascuna riflessione il punto P si mantiene equidistante da O. Quindi descrive un arco di circonferenza
centrato in O. La figura mostra che l'angolo al centro nella doppia riflessione è due volte l'angolo formato
dagli assi l ed m.
Risultato: la composizione di due riflessioni rispetto ad assi l e m concorrenti in O,
formanti fra loro un angolo , è una rotazione attorno ad O, nel verso da l ad m, dell'angolo 2 .