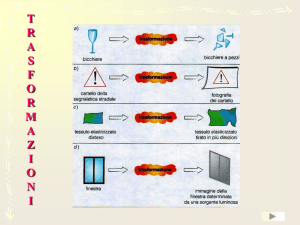
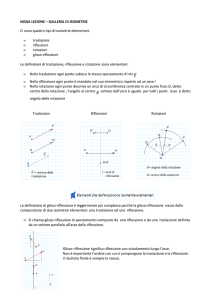
. – Strutture geometriche
PROF.SSA SILVIA PIANTA
OBIETTIVO DEL CORSO
Dare una visione unificante delle geometrie metriche classiche (euclidea,
iperbolica ed ellittica) e dei loro gruppi di isometrie, attraverso l’uso del campo
complesso. Approfondire poi lo studio delle isometrie in ciascuno dei tre casi,
mettendole in relazione con gruppi ortogonali o con sottogruppi notevoli di
proiettività della retta proiettiva complessa.
PROGRAMMA DEL CORSO
– Isometrie del piano e dello spazio euclideo reale e loro rappresentazione come
funzioni di una variabile complessa: punto di vista geometrico, analitico e
algebrico; classificazione delle isometrie di R2, generatori e fattorizzazione del
gruppo; gruppi ortogonali in dimensione 2 e 3 sui reali.
– Isometrie della sfera, inversione circolare e proiettività della retta proiettiva
complessa.
– Piano assoluto reale.
– Piano iperbolico reale e piano ellittico reale e loro gruppi di isometrie.
BIBLIOGRAFIA
R.C. LYNDON, Groups and Geometry, Cambridge University Press, Cambridge, 1987.
J. STILLWELL, Geometry of surfaces, Springer Verlag, Berlin-New York, 1992.
DIDATTICA DEL CORSO
Lezioni in aula.
METODO DI VALUTAZIONE
L'insegnamento prevede una prova orale di accertamento dei risultati di apprendimento.
Tale prova intende accertare il grado di assimilazione dei concetti, dei risultati e delle
procedure illustrate nell'insegnamento tramite esposizione e discussione di alcuni punti del
programma, non escludendo collegamenti fra parti dello stesso o richiami a prerequisiti .
La valutazione della prova terrà conto della correttezza delle procedure illustrate, del
loro rigore logico e metodologico, e della efficacia e correttezza espositiva, valorizzando
l'assimilazione dei concetti e la loro rielaborazione personale da parte del candidato.
AVVERTENZE
La Prof.ssa Silvia Pianta riceve gli studenti dopo le lezioni nel suo studio.