Le trasformazioni geometriche

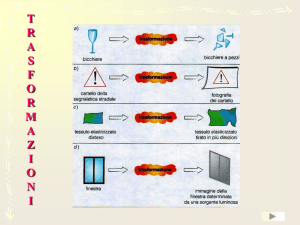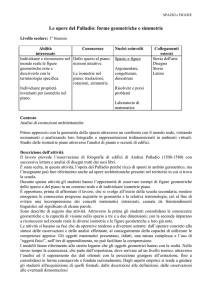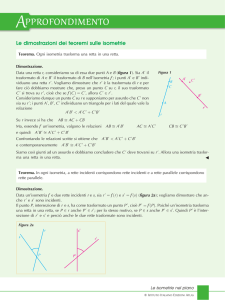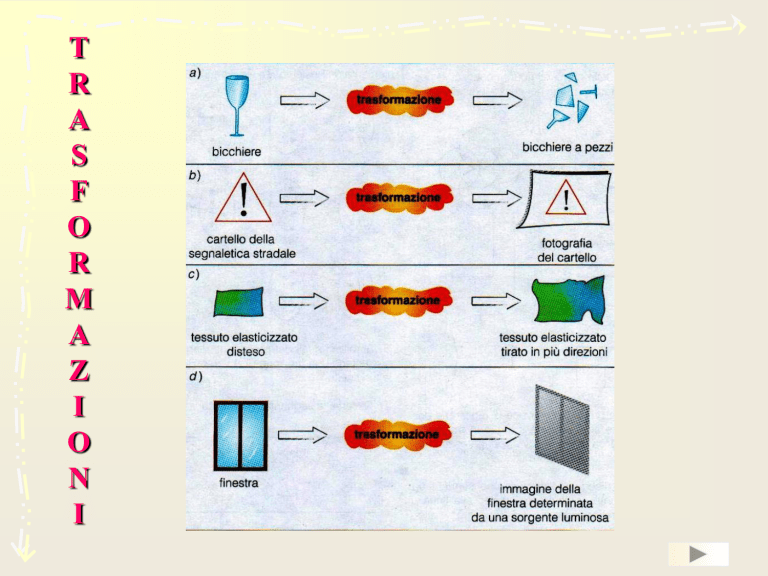
T
R
A
S
F
O
R
M
A
Z
I
O
N
I
La figura rappresenta un’incisione di
M.C.Escher (1898-1972).
Essa fornisce un esempio di
riflessione sulla sfera; è interessante
notare che le linee rette degli spigoli
della stanza dove si trova l’artista
sono diventate linee curve.
LE TRASFORMAZIONI DEL PIANO SONO
1.
CORRISPONDENZE BIUNIVOCHE TRA PUNTI DEL PIANO
Date due figure corrispondenti, ad ogni punto della prima figura
corrisponde uno ed un solo punto delle seconda
2.
COLLINEAZIONI
Ovvero conservano l’allineamento dei punti.
C
D
D
P
A
S
D'
P'
B
A'
C
C'
A=A'
B=B'
B'
D'
C'
Ogni trasformazione si caratterizza per qualche cosa che rimane
invariato, i cosiddetti INVARIANTI
Alcuni invarianti di una trasformazione possono essere
•La lunghezza dei segmenti
•L’ampiezza degli angoli
•Il parallelismo
•Le direzioni
•Il rapporto tra i segmenti
•L’orientamento dei punti del piano
Un punto che nella trasformazione corrisponde a se stesso si dice
unito o fisso.
Una figura che si trasforma globalmente in se stessa, anche se non
tutti i punti sono fissi, si dice unita nella trasformazione.
DUE ESEMPI DI TRASFORMAZIONI
1.
Una trasformazione che consiste in uno spostamento
ovvero un movimento rigido ha come invariante globale
la MISURA delle figure.
Sono suoi invarianti :
•La lunghezza dei segmenti
•L’ampiezza degli angoli
•Il parallelismo
•Il rapporto tra segmenti
Il cavaliere nero è il risultato dell’applicazione, alla
figura di sinistra, di una traslazione.
2.
Una trasformazione che consiste in un ingrandimento o riduzione
ha come invariante globale la FORMA delle figure.
Sono suoi invarianti :
•
L’ampiezza degli angoli
•
Il parallelismo
•
Il rapporto tra segmenti
LE ISOMETRIE
In matematica, e in particolare in geometria, si definisce isometria
(o trasformazione rigida) una trasformazione che non modifica le
distanze tra i punti (e, di conseguenza, le ampiezze degli angoli).
B'
B
F‘
F
A'
A
C
C'
Proprietà delle isometrie
In una isometria:
•a una retta corrisponde una retta
•a rette incidenti corrispondono rette incidenti
•a retta parallele corrispondono rette parallele
•a ogni triangolo corrisponde un triangolo ad esso congruente
•ad ogni angolo corrisponde un angolo ad esso congruente
Quattro particolari isometrie del piano euclideo sono:
•
•
•
•
rotazioni, di cui sono un caso particolare le simmetrie centrali
traslazioni
simmetrie assiali, anche dette riflessioni
antitraslazioni, anche dette glissosimmetrie, glissoriflessioni o
simmetrie con scorrimento (composizione di una simmetria assiale e di una
traslazione di direzione parallela all'asse di simmetria.)
Rotazione
Traslazione
Simmetria assiale
Antitraslazione
-7
Le quattro classi di isometrie del piano possono essere a loro volta
classificate in:
•
•
isometrie invertenti, che comprendono le simmetrie assiali e
le antitraslazioni
isometrie non invertenti o dirette, tra cui si trovano
rotazioni e traslazioni
La simmetria assiale è un'isometria invertente
B'
La rotazione è un'isometria non invertente
B'
50
B
B
C'
A'
A
A
C
C'
A'
C
50
Una generica isometria T, non appartenente ad una di queste
classi, sarà ottenibile come composizione di alcune isometrie che
vi appartengono.
Si può dimostrare un altro risultato interessante:
le simmetrie assiali sono sufficienti per generare tutte le isometrie
ISOMETRIE IN NATURA E NELL’ARTE
In natura si possono individuare forme geometriche
interpretabili assumendo come modello le trasformazioni
isometriche.
Le più frequenti sono la simmetria centrale e la simmetria
assiale, presenti in natura sia nelle forme più elementari quali
le diatomee, i protozoi e i cristalli di neve, sia in fiori, piante,
pesci, uccelli, mammiferi.
Nell’arte sin dall’antichità le trasformazioni isometriche del
piano sono state usate per creare fregi ornamentali e
pavimentazioni, per decorare soffitti e pareti di palazzi, per
disegnare tessuti, per costruire rosoni ed edifici monumentali,
realizzare statue.
fiocchi di neve
medusa
rosoni
porta dei leoni (XV sec a.C.) Micene
fregio
disegno di tessuto
I FREGI
Se si utilizzano due colori, ci sono
solamente 7 motivi lineari che
possono essere ripetuti all’infinito
su una striscia di carta per ottenere
un fregio.
Le 4 operazioni elementari che possono
essere applicate per ottenere un motivo
che si ripete.
Le diverse possibilità si creano agendo
su un motivo di partenza, che non deve
possedere alcuna simmetria, tramite le
seguenti operazioni:
I sette fregi distinti che si possono generare combinando le quattro operazioni
fondamentali. Alle lettere corrispondono le combinazioni di tali operazioni.
I sette possibili tipi di fregio
simmetrico, ciascuno illustrato da
due esempi tratti dalle tradizioni
decorative di diverse culture.
(da: John D. Barrow, L’Universo
come opera d’arte, Rizzoli 1997)