Programmazione di Matematica
Classe 4°F
A.S. 2016-2017
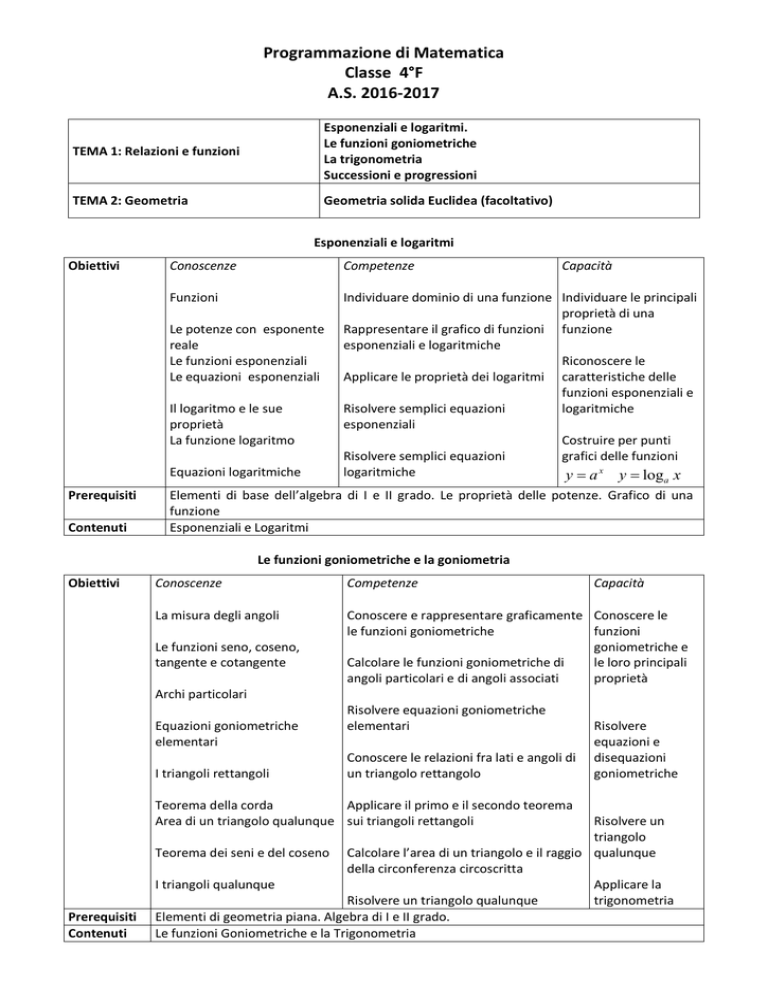
TEMA 1: Relazioni e funzioni
Esponenziali e logaritmi.
Le funzioni goniometriche
La trigonometria
Successioni e progressioni
TEMA 2: Geometria
Geometria solida Euclidea (facoltativo)
Esponenziali e logaritmi
Obiettivi
Conoscenze
Competenze
Funzioni
Individuare dominio di una funzione Individuare le principali
proprietà di una
Rappresentare il grafico di funzioni funzione
esponenziali e logaritmiche
Riconoscere le
Applicare le proprietà dei logaritmi caratteristiche delle
funzioni esponenziali e
Risolvere semplici equazioni
logaritmiche
esponenziali
Costruire per punti
Risolvere semplici equazioni
grafici delle funzioni
logaritmiche
y a x y log x
Le potenze con esponente
reale
Le funzioni esponenziali
Le equazioni esponenziali
Il logaritmo e le sue
proprietà
La funzione logaritmo
Equazioni logaritmiche
Prerequisiti
Contenuti
Capacità
a
Elementi di base dell’algebra di I e II grado. Le proprietà delle potenze. Grafico di una
funzione
Esponenziali e Logaritmi
Le funzioni goniometriche e la goniometria
Obiettivi
Conoscenze
Competenze
La misura degli angoli
Conoscere e rappresentare graficamente Conoscere le
le funzioni goniometriche
funzioni
goniometriche e
Calcolare le funzioni goniometriche di
le loro principali
angoli particolari e di angoli associati
proprietà
Le funzioni seno, coseno,
tangente e cotangente
Capacità
Archi particolari
Equazioni goniometriche
elementari
I triangoli rettangoli
Risolvere equazioni goniometriche
elementari
Conoscere le relazioni fra lati e angoli di
un triangolo rettangolo
Teorema della corda
Applicare il primo e il secondo teorema
Area di un triangolo qualunque sui triangoli rettangoli
Prerequisiti
Contenuti
Risolvere
equazioni e
disequazioni
goniometriche
Risolvere un
triangolo
Teorema dei seni e del coseno Calcolare l’area di un triangolo e il raggio qualunque
della circonferenza circoscritta
I triangoli qualunque
Applicare la
Risolvere un triangolo qualunque
trigonometria
Elementi di geometria piana. Algebra di I e II grado.
Le funzioni Goniometriche e la Trigonometria
Successioni e progressioni
Obiettivi
Conoscenze
Le successioni numeriche
Competenze
Riconoscere una progressione aritmetica
e/o geometrica
Il principio di induzione
Rappresentare una successione: per
enumerazione, con espressione analitica,
per ricorsione
Progressioni aritmetiche
Applicare il principio di induzione
Progressioni geometriche
Determinare i termini di una progressione
noti alcuni elementi
Capacità
Determinare la somma dei primi n termini
di una progressione
Prerequisiti
Contenuti
Inserire termini medi fra due numeri dati
Operazioni e ordinamento in N e Z. Funzioni reali. Equazioni di primo e secondo grado
Le successioni
Il principio di induzione
Le progressioni aritmetiche
Le progressioni geometriche
Geometria solida Euclidea (facoltativo)
Obiettivi
Conoscenze
Competenze
Capacità
Punti rette e piani nello spazio
Valutare la posizione di punti, rette e
piani nello spazio
Conoscere gli
elementi
fondamentali della
geometria solida
euclidea
I poliedri
I solidi di rotazione
Acquisire la nomenclatura relativa ai
solidi nello spazio
Le aree dei solidi notevoli
Calcolare le aree di solidi notevoli
Calcolare aree e
L’estensione e l’equivalenza dei Valutare l’estensione e l’equivalenza di volumi di solidi
solidi
solidi
notevoli
Prerequisiti
Contenuti
I volumi dei solidi notevoli
Calcolare il volume di solidi notevoli
Elementi di geometria piana: triangoli, quadrilateri, circonferenza e cerchio. Congruenze e
similitudini.
Enti dello spazio
Poliedri
Angoloidi
Cilindri, coni e sfera
Aree e volumi di solidi
2
Strumenti e strategie
Lezione frontale
Sollecitazione ad interventi individuali
Lettura del libro di testo
Correzione esercizi assegnati per casa
Attivazione di metodologie di recupero inserite, nei limiti del possibile, nella normale attività didattica
Attività di tutoring da parte di un compagno all interno di un gruppo
Attività di approfondimento con svolgimento di esercizi di livello più complesso o lettura di argomenti
complementari
Valutazione
Verifiche scritte o test alla fine di ogni modulo
Colloqui individuali
Osservazione sistematica della partecipazione attiva al dialogo educativo, che si realizza in interventi,
osservazioni, quesiti posti, ecc.
Osservazione sistematica della quantità, continuità e qualità del lavoro eseguito a casa
La valutazione terrà conto del livello iniziale di preparazione, dell’interesse, della partecipazione e delle capacità di
ogni alunno.
Criteri di valutazione
Si è ritenuto opportuno utilizzare i seguenti indicatori qualitativi:
metodo:
impegno consapevole
uso degli strumenti adeguati
partecipazione al dialogo educativo
espressione:
comunicazione del proprio pensiero e delle conoscenze, sia
nell'esposizione orale che nella produzione scritta
assimilazione dei contenuti:
acquisizione delle informazioni fondamentali
applicazione operativa delle regole e dei concetti
Si è ritenuto opportuno utilizzare i seguenti indicatori quantitativi espressi nella seguente tabella:
3
GRIGLIA DI DESCRIZIONE DEL VALORE NUMERICO DEI VOTI
GIUDIZIO
VOTO
Conoscenza
Comprensione
Capacità
di termini, principi e
regole relativi al
corso di studi attuale
e precedenti
essere in grado di
decodificare il linguaggio
matematico e
formalizzare il linguaggio
di applicare quanto
appreso a situazioni
già note o nuove
Applica
autonomamente e
correttamente le
conoscenze anche a
problemi più
complessi; trova la
soluzione migliore
Applica
autonomamente le
conoscenze anche a
problemi più
complessi in modo
corretto
Sa applicare le
conoscenze in
situazioni nuove ma
commette
imprecisioni
Sa applicare le
conoscenze in
situazioni nuove ma
commette
imprecisioni
Sa applicare le
conoscenze in
situazioni semplici
di routine
Applica le minime
conoscenze con
qualche errore
Eccellente
10
Ottimo
9
Completa e
approfondita
Buono
8
Completa
Discreto
7
Completa degli
elementi di base
Sa leggere e decodificare
in modo autonomo
Sufficiente
6
Limitata agli
elementi di base
Sa leggere e decodificare
solo secondo standards
proposti
Insufficiente
5
Frammentaria e
lacunosa
Sa decodificare solo se
guidato
Gravemente
insufficiente
4
Frammentaria e
gravemente
lacunosa
Sa decodificare solo in
modo parziale
Commette gravi
errori in situazioni
già trattate
3
Sconnessa e
gravemente
lacunosa
Non comprende il
linguaggio specifico
Non riesce ad
applicare le minime
conoscenze
2
Irrilevante
Non comprende il testo
1
Nessuna
Del tutto
insufficiente
Completa e
approfondita
Sa comprendere
situazioni complesse
Sa comprendere
situazioni complesse
Sa leggere e decodificare
in modo autonomo e
personale
Nessuna
4
Non sa cosa fare
Nessuna
Si sarà raggiunto il livello di sufficienza se si saranno conseguiti gli obiettivi minimi in termini di conoscenza, capacità
e competenza:
conoscenza degli elementi di base degli argomenti svolti
applicazione delle conoscenze minime in modo autonomo per affrontare semplici situazioni nuove
esposizione semplice ma corretta.
Livelli minimi di accettabilità in termini di sapere e saper fare
Al termine del 4° anno l’alunno, per raggiungere la sufficienza, deve:
Saper operare con le potenze
Saper definire le funzioni esponenziali e tracciarne il grafico
Saper definire la funzione logaritmo e tracciarne il grafico
Saper risolvere semplici equazioni esponenziali
Saper risolvere semplici disequazioni logaritmiche
Conoscere le funzioni goniometriche e le loro principali proprietà
Saper Risolvere equazioni goniometriche elementari
Saper risolvere un triangolo
Saper applicare i teoremi del seno, del coseno e della corda
Saper definire una successione per ricorrenza o in modo analitico
Saper valutare se una successione è una progressione aritmetica o geometrica
Saper ricavare le formule che legano due termini qualsiasi di una progressione aritmetica o geometrica
Conoscere gli elementi fondamentali della geometria solida euclidea
Riconoscere proprietà di rette e piani nello spazio.
Saper calcolare aree e volumi di alcuni solidi notevoli
Il docente
Prof.ssa Valentina Bartolini
Roma, 20/10/2016
5