Applicazioni del teorema di Gauss:
campo elettrico generato da un filo di lunghezza infinita e spessore infinitesimo,
caricato con densita’ lineare di carica λ costante
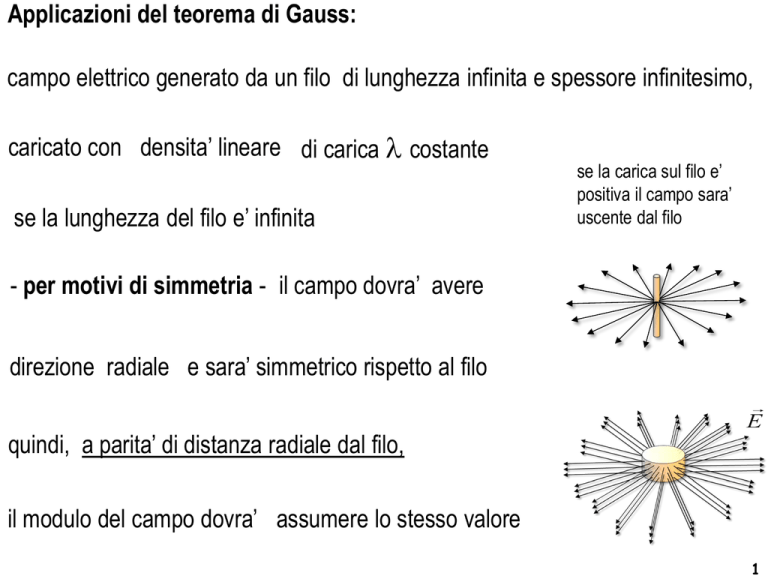
se la lunghezza del filo e’ infinita
se la carica sul filo e’
positiva il campo sara’
uscente dal filo
- per motivi di simmetria - il campo dovra’ avere
direzione radiale e sara’ simmetrico rispetto al filo
quindi, a parita’ di distanza radiale dal filo,
il modulo del campo dovra’ assumere lo stesso valore
1
per determinare l’andamento del modulo del campo
visto dall’ ∞
in funzione della distanza radiale dal filo
sfrutteremo il teorema di Gauss e come superficie chiusa Σ
( superficie gaussiana ) su cui calcolare il flusso Φ Σ ( E ) del campo elettrico E
assumemo un cilindro di raggio r ed altezza L coassiale al filo
2
dividiamo la superficie Σ del cilindro in
superfici infinitesime dS che orienteremo
dS
positivamente verso l’esterno secondo la
r
E
convenzione di orientamento delle superfici chiuse
ΦΣ ( E=
)
∫
E ⋅ dS
dS E
L
Σ
3
ΦΣ ( E ) = ∫ E⋅dS +
superficie base
inferiore cilindro
∫
E⋅dS +
superficie laterale
cilindro
∫
E⋅dS
superficie base
superiore cilindro
sulle due superfici di base del cilindro il flusso
dS
r
sara’ nullo, perche’ il campo e’ perpendicolare
E
dS E
all’orientamento della superficie
L
sulla superficie laterale il modulo E del campo elettrico
Φ ( E ) = ∫ E⋅dS = E
sup laterale
cilindro
∫
dS
sup laterale
cilindro
= E 2π rL
4
da
dq
λ=
dl
dq = λ dl
la carica qint racchiusa all’interno della
superficie gaussiana e’ tutta quella posta sul tratto di lunghezza L del filo
quindi
qint = ∫ λ dl = ∫ λ dl
L
e dato che λ e’ costante
0
L
qint = λ ∫ dl = λ L
0
5
per il teorema di Gauss
qint
Φ( E ) =
ε0
λ
L
dunque Φ ( E ) =
ε0
ma si aveva anche Φ ( E ) = E 2π rL
uguagliando
λL
E 2π rL =
ε0
1 λ
E=
2πε 0 r
6
Backup Slides
7












