SCHEDE DI MATEMATICA FINANZIARIA 1
Introduzione
Matematica finanziaria: la matematica applicata agli scambi di denaro che capitano in momenti lontani nel tempo.
Le stesse formule si possono applicare anche ad altri fenomeni, come si mostrerà con qualche esempio in seguito.
Gli scambi di denaro lontani nel tempo non sono confrontabili direttamente; un esempio: se avrò un certo capitale fra 3
anni invece che oggi, dovrò rinunciare a tutto quello che potrei fare con quel capitale in questi 3 anni (come minimo, tenerlo
in banca a maturare interessi; come massimo, spenderlo per comprarmi il necessario a non morire di fame) e ciò conta
parecchio.
Se avere denaro ora è diverso (meglio) che avere denaro nel futuro, il denaro di oggi e quello di domani sono confrontabili non
direttamente, ma soltanto dopo che si è definito quanto sia il vantaggio di averlo oggi.
Nella matematica finanziaria svolta in queste lezioni, si stabilisce che il vantaggio di avere denaro presto sia sempre
quantificabile e che si identifichi con gli interessi.
Calcolo degli interessi in economia aziendale
Le formule usate in economia aziendale per il calcolo degli interessi sono della forma
I
Crs
g 00
(so che di solito per il tempo si usa il simbolo t e non s, ma qui il simbolo t verrà usato in un significato più adeguato ai
calcoli successivi, come si capisce più avanti).
Al solito, I indica il valore degli interessi, C quello del capitale e r è il tasso d’interesse in percentuale a cui è stato tolto il
simbolo %, mentre g vale 1 se s si calcola in anni, 12 se s si calcola in mesi, 365 se s si calcola in giorni e così via.
Numeri percentuali e numeri unitari
Fra i numeri percentuali p% e quelli unitari u (cioè i normali numeri in forma decimale), il legame è u = p/100, o anche p =
100u.
Esempi:
se p% è 2%, allora u è 0,02;
se u è 0,34, allora p% è 34%.
Sono particolarmente significativi questi casi:
p% = 100% equivale a u = 1 e viceversa;
p% = 50% equivale a u = 0,5 e viceversa.
Quindi: invece del vecchio r%/100 di economia aziendale, useremo il nuovo r di matematica finanziaria.
Conteggio del tempo
Quando si misura il tempo, è essenziale chiarire quale sia l’unità di misura: giorni, settimane, mesi, trimestri, quadrimestri,
semestri, anni, decenni o altro?
Esempi:
* se il periodo in cui misuro il tempo è l’anno, quando ho 8 mesi ho 8 dodicesimi (non DECIMI!) di anno, cioè 8/12 = 2/3
= 0,666... = 66,67% di anno; perciò 8 mesi sono i 2/3 di un anno, o anche il 66,67% di un anno;
* quando ho 615 giorni ho 615/365 = 1,6849 = 168,49% di anno, perciò 615 giorni sono i 615/365 = 123/73 di un anno, o
anche il 168,49% di un anno.
Indicare una durata con un numero puro, come 5,3, non basta: bisogna specificare se quel 5,3 indica anni, mesi, secoli...
Se ho una durata s in una certa misura, ad esempio in mesi, e la voglio esprimere in un’altra misura, ad esempio in trimestri,
devo dividere s per il numero di mesi che stanno in un trimestre: durata in trimestri = durata mesi/3. Infatti un mese è un
terzo di trimestre...
Per stabilire con chiarezza la regola generale, conviene introdurre il concetto di frequenza: la frequenza di un periodo è il
numero di periodi che servono per fare un anno. Ecco una scheda utile per fissare le idee.
1
La frequenza di un giorno è 360 nell’anno commerciale e 365 nell’anno civile.
La frequenza di una settimana è convenzionalmente fissata in 52.
La frequenza di un mese è 12.
La frequenza di un bimestre è 6.
La frequenza di un trimestre è 4.
La frequenza di un quadrimestre è 3.
La frequenza di un semestre è 2.
La frequenza di un anno è 1.
La frequenza di un biennio è 0,5.
La frequenza di un lustro (o quinquennio) è 0,2.
La frequenza di un decennio è 0,1.
In generale, se ho una durata s misurata in periodi di frequenza g e voglio trovare la durata equivalente t misurata in periodi
di frequenza f, la regola è t = s/(g/f). Naturalmente, questa regola nasce dalla proporzione t : f = s : g.
Esempio: ho una durata s di 5 quadrimestri (perciò è g = 3) e voglio trovare l’equivalente durata t in semestri (perciò è f = 2).
Dato che è g/f = 1,5 (serve un quadrimestre e mezzo per fare un semestre), la durata cercata sarà t = 5/1,5 = 3,333...
Esempio più ricco: quanti anni si ottengono, con l’anno civile, sommando 3 anni e mezzo, due quadrimestri e 18 giorni?
Tre anni e mezzo sono 3,5 anni; due quadrimestri sono 2/3 = 0,666... di anno; 18 giorni con l’anno civile sono 18/365 =
0,049315 di anno; in totale, la durata in anni è 3,5+0,666...+0,049315 = 4,215982.
Esempio ulteriore: in mesi, quanto vale il risultato precedente?
Sarà 4,21598212 = 50,59178 mesi.
Legame con il calcolo degli interessi come trattato in matematica
finanziaria
In matematica finanziaria, la formula degli interessi viene scritta in modo un po’ diverso da quello usato in economia
aziendale; i passaggi sono questi:
I
Crs
Crs
r s
. In altri termini, gli interessi si ottengono
C
g 00 g 100
100 g
moltiplicando il capitale C per il tasso d’interesse r/100, quindi già in forma unitaria, e per la misura del tempo in anni s/g.
Questa misura è coerente con la regola mostrata sopra: dato che si sta cercando la misura in anni, si applicherà la formula t =
s/(g/1), cioè t = s/g.
Di solito, il tasso d’interesse in forma unitaria in matematica finanziaria è indicato con i.
In queste lezioni si farà diversamente: d’ora in poi, per evitare nuovi simboli, si userà r per indicare anche la forma unitaria
del tasso d’interesse. Nella mia esperienza, ciò non ha mai creato difficoltà nell’apprendimento, anzi.
La formula di economia aziendale qui diventa
I Crt .
Gli interessi si ottengono moltiplicando il capitale per il tasso, già in forma unitaria, e per la durata, già espressa nella corretta
unità di misura.
Sia chiaro che tasso e durata devono avere sempre la stessa unità di misura del tempo.
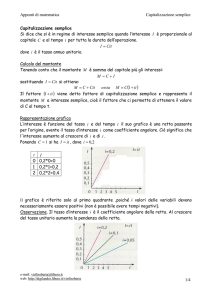
Interessi semplici e composti
Il montante è il capitale a cui sono stati aggiunti gli interessi: M = C+I. Sapendo che è I = Crt, si può sostituire, ottenendo M
= C+Crt. Se si raccoglie a fattor comune, si arriva a
M = C(1+rt).
Questa è la formula di capitalizzazione semplice. Perché l’aggettivo ‘semplice’? Perché gli interessi si calcolano sempre sul
“semplice” capitale iniziale e non maturano a loro volta interessi. Il regime di capitalizzazione semplice è valido di solito per
calcolare gli interessi per periodi brevi; ad esempio, per un trimestre, sui conti correnti bancari.
L’argomento è già stato trattato in economia aziendale e pertanto qui non verrà ripreso seriamente. Comunque, si segnala
che, volendo trovare il capitale dato il montante, bisognerà invertire la formula, ottenendo C = M/(1+rt).
Spesso, quando si lavora con quest’ultima formula, si pensa a M come ad un capitale dato futuro e a C come ad un incognito
valore attuale (cioè quanto si è disposti a spendere oggi per ottenere un capitale in futuro). Questo regime è chiamato di
attualizzazione semplice o di sconto razionale.
Molto più interessante, utile e sensata invece è la capitalizzazione composta, quella cioè in cui gli interessi maturano a loro volta
interessi; su questa ci dilungheremo parecchio.
2
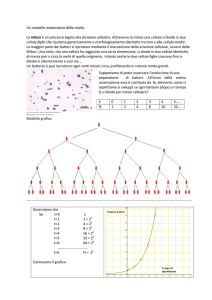
Calcolo di un montante composto
Per questo calcolo, si parte dall’ipotesi che il capitale maturi interessi per periodi interi, perciò sarà t = 1.
La novità, e anche la complicazione, sta nel fatto che alla fine di ogni periodo il capitale è diverso, perché comprende anche
gli interessi maturati nei periodi precedenti; quindi il capitale C misurato alla fine del periodo t sarà indicato con Ct . È il caso
di segnalare che C0 indica un capitale alla fine del periodo 0, cioè all’inizio del periodo 1.
Quindi la formula di capitalizzazione è data da Ct+1 = Ct+rCt , cioè, raccogliendo Ct a fattor comune, da
Ct+1 = Ct(1+r);
il significato è: se su un capitale Ct faccio maturare interessi per un periodo, cioè lo moltiplico per 1+r, dopo un periodo
ottengo un capitale Ct+1 .
Questa formula tuttavia non è comoda per il calcolo, perché se devo capitalizzare per 10 periodi devo ripeterne l’uso per 10
volte; e non pensiamo a quando l’incognita del problema è il tempo! Ma si può ottenere un equivalente molto migliore, nel
modo che segue.
Poniamo t = 0; la formula diventa C1 = C0(1+r).
Poniamo t =1; la formula diventa C2 = C1(1+r). Ma, dato che abbiamo appena trovato qual è la formula di C1 , possiamo
sostituirla e ottenere C2 = [C0(1+r)](1+r), cioè C2 = C0(1+r)2.
Poniamo t = 2; la formula diventa C3 = C2(1+r). Ma dato che abbiamo appena trovato qual è la formula di C2 , possiamo
sostituirla e ottenere C3 = [C0(1+r)2](1+r), cioè C3 = C0(1+r)3.
Continuando così, per un numero n qualunque di volte, si arriva a
Cn = C0(1+r)n.
Questa è la formula fondamentale per i calcoli in capitalizzazione composta.
Ecco alcuni esempi di come usarla.
* Investo 2300 euro per 5 anni, al tasso del 3% annuo; di quanto disporrò alla fine?
I dati sono C0 = 2300, n = 5, r = 3% = 0,03; il montante è quindi C5 = 2300(1+0,03)5 = 2666,33 euro.
* Chiedo un prestito di 1000 euro, al tasso del 2,1% semestrale, da rimborsare in blocco fra 2 anni; quanto dovrò pagare alla
fine?
I dati sono C0 = 1000, r = 2,1% = 0,021, n = 22 =4 (ATTENZIONE! Il tasso è semestrale, quindi il tempo va misurato in
semestri, cioè con f = 2); il montante quindi è C4 = 1000(1+0,021)4 = 1086,68 euro.
* Non è obbligatorio usare questa formula soltanto in ambito finanziario: oggi compro un litro di latte con 1,30 euro; il tasso
d’inflazione è di circa il 2,5%; fra 10 anni, quanto mi aspetto che costerà un litro di latte?
I dati sono C0 = 1,3, r = 2,5% = 0,025, n = 10; il montante quindi è C10 = 1,3(1+0,025)10 = 1,66 euro.
* Non è obbligatorio usare questa formula soltanto in ambito economico: in un certo parco nazionale, ci sono 14 orsi; questi
si riproducono ad un tasso annuo del 2%, quanti orsi ci saranno verosimilmente fra 20 anni?
I dati sono C0 = 14, r = 2% = 0,02, n = 20; il montante quindi è C20 = 14(1+0,02)20 = 20,8 orsi.
* Le lasagne, appena tolte dal forno, sono a circa 180° sopra la temperatura ambiente e si raffreddano ad un tasso del 30%
ogni minuto (dato inventato); fra 8 minuti, di quanto saranno più calde della temperatura ambiente?
I dati sono C0 = 180, r = 30% = 0,3 (ATTENZIONE! Le lasagne si raffreddano, perciò il tasso è negativo!), n = 8; il
montante quindi è C8 = 180(10,3)8 = 10,38°.
La formula può essere usata per tutti i fenomeni in cui qualcosa cambia ad un tasso costante (nell’ultimo esempio, Newton ha
mostrato che la differenza di temperatura di un corpo col suo ambiente varia ad un tasso costante).
La capitalizzazione composta aumenta il montante molto più di quanto faccia la capitalizzazione semplice; ciò è tanto più
evidente quanto maggiore è il tasso e quanto maggiore è il tempo di capitalizzazione.
Esempio: dato un capitale di 100 euro, qual è il montante al tasso dell’8% dopo 10 anni in regime composto? E in regime
semplice?
In regime composto, si ottiene il montante C10 = 100(1+0,08)10 = 215,89.
In regime semplice, si ottiene il montante M = 100(1+0,0810) = 180.
Una variazione sul tema: la crescita logistica
La formula di capitalizzazione composta mostra un capitale che aumenta per sempre e sempre più velocemente.
Naturalmente tutto ciò non è possibile nella realtà, ma è accettabile quando si lavora con grandezze lontane dal loro
massimo possibile, come i capitali di famiglie e imprese. Se invece si lavora con grandezze per le quali il massimo possibile
(che nel seguito sarà chiamato capienza) non è poi tanto lontano, l’andamento non può più essere quello della
capitalizzazione composta.
3
Esempi: se trattiamo della crescita di una popolazione (umana, vegetale, batterica e simili) nel suo ambiente, il massimo
possibile di popolazione su un dato territorio si raggiunge in tempi contenuti; se trattiamo della crescita di una pianta, la
massima altezza possibile si raggiunge al massimo in decenni; se trattiamo di un’epidemia, il massimo numero di contagiati si
raggiunge presto.
Ecco un modo (non l’unico, ma il più naturale) per trattare di simili fenomeni: indicando con K la capienza di una certa
grandezza, la differenza KCt indica per quanto ancora la grandezza Ct può aumentare o, cambiando semplicemente unità di
misura, le risorse di Ct ancora disponibili per l’aumento.
Quindi Ut = Ct/(KCt) misura la grandezza che aumenta non in assoluto, ma rispetto alle risorse ancora disponibili; questa
grandezza relativa, diversamente da quella assoluta, può crescere per sempre, perché aumenta anche quando c’è una
semplice riduzione di risorse disponibili. Si può anche interpretare Ut come la difficoltà con cui cresce Ct .
Poniamo che sia questa grandezza relativa, o questa difficoltà di crescita, che aumenta ad un tasso costante, perciò si ha Ut+1
= (1+r)Ut .
Questa formula ha la stessa struttura di Ct+1 = Ct(1+r), pertanto potrà essere trattata allo stesso modo e dare Un = U0(1+r)n.
Sostituendo Un = Cn/(KCn) in questa formula, si ottiene
Cn
C0
1 r n .
K Cn K C0
Ora bisogna rendere esplicita Cn ; ecco i passaggi:
* si sostituisce la pesante espressione
C0
1 r n con la semplice lettera A (passaggio lecito perché l’espressione in
K C0
questione con contiene l’incognita Cn), in modo da ridurre la formula sopra alla più semplice
Cn
A.
K Cn
* si isola Cn , mediante i passaggi che seguono:
* si moltiplica ambo i membri per KCn , ottenendo
Cn AK Cn ;
* si svolge la parentesi con Cn , ottenendo Cn AK ACn ;
* si portano a sinistra i termini con Cn e a destra quelli senza, ottenendo
Cn ACn AK ;
Cn 1 A AK ;
AK
K
* si divide ambo i membri per la parentesi, ottenendo Cn
;
1 A 1 1
A
* si raccoglie a fattor comune Cn , ottenendo
* una volta ultimati i calcoli per isolare Cn , si reintroduce al posto di A l’intera espressione
Cn
K
1
1
C0
1 r n , arrivando a
K C0
;
C0
1 r n
K C0
* si nota che la frazione C0/(KC0) è al denominatore, quindi può essere “ribaltata”; inoltre, si può usare un esponente
negativo per 1+r, ottenendo finalmente
Cn
K
.
K C0
n
1 r
1
C0
Questa funzione di n si chiama logistica e mostra come può cambiare una crescita esponenziale, come ad esempio la
capitalizzazione composta, quando la grandezza che cresce ha una capienza.
Esempio: il tasso per periodo a cui cresce una popolazione di 10 batteri è il 25%. Indicare la quantità di batteri dopo 20
periodi, sia in un ambiente illimitato, sia in un ambiente in cui al massimo possono stare 1000 batteri.
I dati sono: C0 = 10, r = 25% = 0,25, n = 20, K = 1000; nell’ambiente illimitato, si ha un montante di C20 = 10(1+0,25)20 =
867,36; nell’ambiente con capienza 1000, si ha C20
1000
1000 10
1 0,25 20 1
10
466,99 .
4
Esempio: la popolazione di un certo comune con forte immigrazione oggi ha 41.456 residenti, mentre 8 anni fa ne aveva
39.665. Se il tasso di crescita è il 2% annuo, qual è la capienza del comune? Cioè, a quante persone si presume che possa
arrivare?
Dati: n = 8, C8 = 41.456, C0 = 39.665, r = 0,02.
Conviene cominciare a isolare K prendendo la formula nella forma
da ottenere
Cn
C0
1 r n e “ribaltandola”, in modo
K Cn K C0
K C n K C0
1 r n ; da qui si arriva subito a K 1 K 11 r n e quindi a
Cn
C0
Cn
C0
K
K
1 r n 1 r n .
1
Cn
C0
Spostando i termini con K a sinistra dell’uguale, gli altri a destra e raccogliendo K a fattor comune, si ha
n
1 1 r n
1 1 r
n
K
1
1
r
;
la
formula
utile
per
il
calcolo
dunque
è
.
K
n
C
C
1
1
r
n
0
Cn
C0
Chi non volesse usare esponenti negativi, può sempre moltiplicare numeratore e denominatore per (1+r)n, ottenendo
K
1 r n 1
1 r n 1
Cn
.
C0
Sostituendo ora i dati, si ottiene K
1,028 1
56.252,66 .
1,028
1
41.456 39.665
Le formule inverse per la capitalizzazione composta
Torniamo alla formula di capitalizzazione composta. In essa ci sono quattro variabili, Cn , C0 , r e n, ciascuna delle quali è una
possibile incognita.
* Se l’incognita è Cn , basta la solita formula diretta di capitalizzazione composta.
Gli esempi sopra illustrano bene il punto.
* Se l’incognita è C0 , basta dividere per (1+r)n per ottenere
C0
Cn
.
1 r n
Esempio: fra 3 anni, incasserò un credito di 3000 euro; se voglio avere subito denaro liquido e sconto il credito in banca al
4%, quanto ottengo?
Dati: n = 3; C3 = 3000, r = 4% = 0,04; il valore attuale è C0 = 3000/(1+0,04)3 = 2666,99 euro.
In certi problemi, non è facile capire se ciò che si deve trovare è C0 o Cn . Ecco uno schema che può favorire la decisione
giusta.
Disegnamo l’asse del tempo, che va sempre da sinistra (passato) a destra (futuro), con le formule da usare nei vari casi.
Asse del tempo: Passato Presente Futuro
Formule da usare:
C0 1 r
n
Cn
1 r n
CAPITALE MONTANTE VALORE ATTUALE CAPITALE
(passato)
(presente)
(futuro)
5
* Se l’incognita è r, servono 3 passaggi: primo, si divide ambo i membri per C0 , ottenendo 1 r
n
radice ennesima su ambo i membri, ottenendo
1 r n
Cn
; secondo, si fa la
C0
Cn
(si prende sempre col segno positivo, perché 1+r negativo
C0
non ha molto senso); terzo, si sottrae 1 da ambo i membri, ottenendo
rn
Cn
1.
C0
Esempio: il valore nominale dei BOT è convenzionalmente 100, mentre il loro valore di mercato è minore di 100; se ad
esempio un BOT costa tutto compreso 97,8 e mancano 240 giorni alla scadenza, qual è il tasso annuo effettivo d’interesse?
Dati: n = 240/365 (se il tasso è annuo, bisogna convertire il tempo in anni) = 0,657534; C0,657534 = 100, C0 = 97,8.
1
100 0, 657534
1 0,0344 3,44% .
Il tasso è r
97,8
Esempio: compro un titolo a 130 e dopo un anno lo rivendo a 110. Qual è il tasso di profitto annuo?
Dati: C0 = 130; n = 1; C1 = 110.
Il tasso è r = (110/130)1 = 0,1539. Si ha quindi un tasso di perdita del 15,39%.
* Se l’incognita è n, servono questi passaggi: primo, si divide ambo i membri per C0 , ottenendo 1 r
n
Cn
; secondo, si
C0
esplicita n, ottenendo n = log(1+r)(Cn/C0); terzo, si cambia la base, ottenendo
Cn
C0
.
n
log 10 1 r
log 10
Esempio: investo 2500 euro al 2,5% annuo; se mi servono 3000 euro, fra quanto tempo potrò incassare?
3000
2500 7,38365 .
Dati, C0 = 2500, r = 3% = 0,025, Cn = 3000; il tempo (in anni) è n
log 10 1,025
log 10
Questo risultato è in anni, ma a me serve convertirlo in anni, mesi e giorni; perciò comincio a notare che stiamo trattando di
7 anni e di una quota di anno pari a 0,38365; a quanto corrisponde in mesi? a 0,3836512, cioè 4,6038 mesi; abbiamo quindi
4 mesi e una quota di mese pari a 0,6038; quanto fa in giorni? Assumendo l’anno commerciale, si ha 0,603830, cioè 18,114
giorni, che si può approssimare a 18 giorni, dato che le scadenze dei contratti di credito si misurano in date e non in orari.
I tassi equivalenti
Tasso e durata devono sempre essere nella stessa unità di misura: se il tasso è annuo, la durata è in anni; se il tasso è mensile,
la durata è in mesi; e così via. Finora si è trattato il caso in cui si teneva fissa l’unità di misura del tasso e si faceva variare
quella della durata, ma ora si mostrerà che è possibile anche l’inverso.
Il punto è che il tasso con una certa frequenza deve risultare del tutto equivalente a quello con un’altra frequenza. Quando
due tassi sono equivalenti? Quando, partendo dallo stesso capitale, danno lo stesso montante.
Se ho un certo capitale C e voglio investirlo per un anno con capitalizzazione di frequenza f, con un tasso rf otterrò un certo
montante M; in formule, M = C(1+rf )f.
Se cambia la frequenza, che diventa g, ma voglio partire dallo stesso capitale C per arrivare allo stesso montante M, dovrò
cambiare il tasso in un nuovo tasso rg ; in formule, M = C(1+rg )g.
Dato che entrambi i montanti sono uguali a M, le capitalizzazioni saranno anch’esse uguali, perciò si ha C(1+rf )f = C(1+rg )g.
Semplificando C, si ottiene
(1+rf )f = (1+rg )g.
Volendo esplicitare rf , si ha, con i soliti calcoli per le formule inverse,
6
rf = (1+rg )g/f1.
Esempio: qual è il tasso annuo che equivale al 4% trimestrale?
Si cerca rf , perciò è f = 1; si ha rg = 0,04, perciò è g = 4; quindi risulta r1 = (1+0,04)4/11 = 0,1699 = 16,99% annuo.
Esempio: qual è il tasso mensile che equivale al 3,5% semestrale?
Si cerca rf , perciò è f = 12; si ha rg = 0,035, perciò è g = 2; quindi risulta r12 = (1+0,035)2/121 = 0,00575 = 0,575% mensile.
Esempio: qual è il tasso biennale che equivale al 5,5% annuo?
Si cerca rf , perciò è f = 0,5; si ha rg = 0,055, perciò è g = 1; quindi risulta r0,5 = (1+0,055)1/0,51 = 0,113 = 11,3% annuo.
7