SCHEDA DI SINTESI: CIRCONFERENZA E CERCHIO
PROF.SSA STEFANIA SCIUTO
LA CIRCONFERENZA
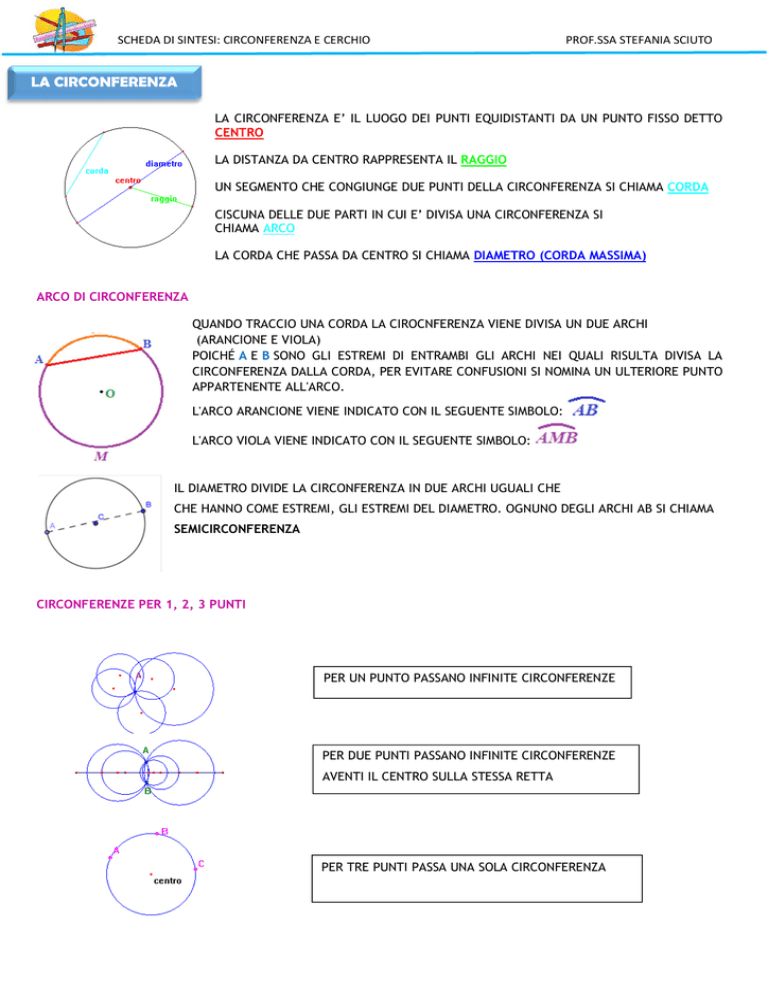
LA CIRCONFERENZA E’ IL LUOGO DEI PUNTI EQUIDISTANTI DA UN PUNTO FISSO DETTO
CENTRO
LA DISTANZA DA CENTRO RAPPRESENTA IL RAGGIO
UN SEGMENTO CHE CONGIUNGE DUE PUNTI DELLA CIRCONFERENZA SI CHIAMA CORDA
CISCUNA DELLE DUE PARTI IN CUI E’ DIVISA UNA CIRCONFERENZA SI
CHIAMA ARCO
LA CORDA CHE PASSA DA CENTRO SI CHIAMA DIAMETRO (CORDA MASSIMA)
ARCO DI CIRCONFERENZA
QUANDO TRACCIO UNA CORDA LA CIROCNFERENZA VIENE DIVISA UN DUE ARCHI
(ARANCIONE E VIOLA)
POICHÉ A E B SONO GLI ESTREMI DI ENTRAMBI GLI ARCHI NEI QUALI RISULTA DIVISA LA
CIRCONFERENZA DALLA CORDA, PER EVITARE CONFUSIONI SI NOMINA UN ULTERIORE PUNTO
APPARTENENTE ALL'ARCO.
L'ARCO ARANCIONE VIENE INDICATO CON IL SEGUENTE SIMBOLO:
L'ARCO VIOLA VIENE INDICATO CON IL SEGUENTE SIMBOLO:
IL DIAMETRO DIVIDE LA CIRCONFERENZA IN DUE ARCHI UGUALI CHE
CHE HANNO COME ESTREMI, GLI ESTREMI DEL DIAMETRO. OGNUNO DEGLI ARCHI AB SI CHIAMA
SEMICIRCONFERENZA
CIRCONFERENZE PER 1, 2, 3 PUNTI
PER UN PUNTO PASSANO INFINITE CIRCONFERENZE
PER DUE PUNTI PASSANO INFINITE CIRCONFERENZE
AVENTI IL CENTRO SULLA STESSA RETTA
PER TRE PUNTI PASSA UNA SOLA CIRCONFERENZA
SCHEDA DI SINTESI: CIRCONFERENZA E CERCHIO
PROF.SSA STEFANIA SCIUTO
PROPRIETÀ DELLA CORDA
1
LA PERPENDICOLARE CONDOTTA DAL CENTRO DI UNA CIRCONFERENZA AD UNA CORDA
LA DIVIDE A METÀ
AOB È UN TRIANGOLO ISOSCELE (HA SICURAMENTE DUE LATI UGUALI CHE COINCIDONO
CON I RAGGI) E OH RAPPRESENTA SIA L’ALTEZZA CHE LA MEDIANA PERCHÉ NEL
TRIANGOLO ISOSCELE ALTEZZA E MEDIANA COINCIDONO.
QUINDI OH È PERPENDICOLARE ALLA BASE AB E LA DIVIDE A METÀ
2
DUE CORDE CONGRUENTI HANNO UGUALE DISTANZA DAL CENTRO E, VICEVERSA, DUE CORDE CHE HANNO L
ASTESSA DISTANZA DAL CENTRO SONO CONGRUENTI
LE BASI DEI DUE TRIANGOLI AOB E COD SONO CONGRUENTI DATO CHE ALL'INIZIO
ABBIAMO DISEGNATO DUE CORDE CONGRUENTI.
INOLTRE OA = OB = OC = OD perché RAGGI DELLA CIROCONFERENZA
DI CONSEGUENZA, I DUE TRIANGOLI AOB E COD SONO CONGRUENTI.
SE I DUE TRIANGOLI SONO CONGRUENTI, ANCHE LE LORO ALTEZZE OH E OK SONO CONGRUENTI
SCHEDA DI SINTESI: CIRCONFERENZA E CERCHIO
PROF.SSA STEFANIA SCIUTO
CIRCONFERENZE E RETTE
RETTA ESTERNA AD UNA CIRCONFERENZA
LA RETTA ESTERNA AD UNA CIRCONFERENZA:
NON HA ALCUN PUNTO IN COMUNE CON LA CIRCONFERENZA
LA DISTANZA h TRA LA RETTA E IL CENTRO È MAGGIORE AL RAGGIO
RETTA SECANTE AD UNA CIRCONFERENZA
LA RETTA SECANTE AD UNA CIRCONFERENZA:
HA DUE PUNTI IN COMUNE CON LA CIRCONFERENZA: PUNTO P E PUNTO Q
LA DISTANZA h TRA LA RETTA E IL CENTRO È MINORE DEL RAGGIO r
ETIMOLOGIA
SECANTEM È PARTICIPIO PASSATO DI SECARE = TAGLIARE.
SECANTE = LINEA CHE TAGLIA IN PIÙ PARTI UNA CIRCONFERENZA
RETTA TANGENTE AD UNA CIRCONFERENZA
LA RETTA TANGENTE AD UNA CIRCONFERENZA:
HA SOLO UN PUNTO IN COMUNE CON LA CIRCONFERENZA: PUNTO P
LA DISTANZA h TRA LA RETTA E IL CENTRO È CONGRUENTE AL RAGGIO r
ETIMOLOGIA
TANGENTEM È PARTICIPIO PRESENTE DI TANGERE = TOCCARE, CHE TOCCA.
TANGENTE = LINEA CHE TOCCA UNA CIRCONFERENZA)
PROPRIETÀ DELLE TANGENTI
IL RAGGIO r CONDOTTO DAL CENTRO AL PUNTO DI TANGENZA (PUNTO A) È
PERPENDICOLARE ALLA RETTA TANGENTE
I SEGMENTI DI TANGENZA AP E BP SONO
I TRIANGOLO OAP È UGUALE AL TRIANGOLO OBP CONGRUENTI
OAP E OBP SONO TRIANGOLI RETTANGOLI
AP = BP
SCHEDA DI SINTESI: CIRCONFERENZA E CERCHIO
PROF.SSA STEFANIA SCIUTO
POSIZIONI RECIPROCHE DI DUE CIRCONFERENZE
DUE CIRCONFERENZE POSSONO ESSERE:
SECANTI;
UNA ESTERNA ALL'ALTRA O UNA INTERNA ALL'ALTRA;
TANGENTI INTERNAMENTE O ESTERNAMENTE;
CONCENTRICHE.
CIRCONFERENZE SECANTI
DUE CIRCONFERENZE SI DICONO SECANTI SE HANNO DUE PUNTI IN COMUNE.
1
INDICHIAMO:
LA DISTANZA TRA I CENTRI DELLE DUE CIRCONFERENZE CON OO';
IL RAGGIO r DELLA CIRCONFERENZA C, CON OA
IL RAGGIO r’ DELLA CIRCONFERENZA C’, CON O’A
POSSIAMO AFFERMARE CHE:
OO' < r + r'
DUE CIRCONFERENZE SONO SECANTI SE LA DISTANZA DEI LORO
CENTRI È MINORE DELLA SOMMA DEI LORO RAGGI
2
CIRCONFERENZE ESTERNE
DUE CIRCONFERENZE SI DICONO ESTERNE SE NON HANNO NESSUNO PUNTO IN COMUNE
INDICHIAMO:
LA DISTANZA TRA I CENTRI DELLE DUE CIRCONFERENZE CON OO'
IL RAGGIO r DELLA CIRCONFERENZA C, CON OA
IL RAGGIO r’ DELLA CIRCONFERENZA C’, CON O’A’
POSSIAMO AFFERMARE CHE:
OO' > r + r'
DUE CIRCONFERENZE SONO ESTERNE SE LA DISTANZA DEI LORO
CENTRI È MAGGIORE DELLA SOMMA DEI LORO RAGGI
3
CIRCONFERENZE INTERNE
INDICHIAMO:
LA DISTANZA TRA I CENTRI DELLE DUE CIRCONFERENZE CON OO'
IL RAGGIO r DELLA CIRCONFERENZA C, CON OA
IL RAGGIO r’ DELLA CIRCONFERENZA C’, CON O’A’
POSSIAMO AFFERMARE CHE:
OO' < r - r'
DUE CIRCONFERENZE SONO INTERNE SE LA DISTANZA DEI
LORO CENTRI È MINORE DELLA DIFFERENZA DEI LORO RAGGI
SCHEDA DI SINTESI: CIRCONFERENZA E CERCHIO
4
PROF.SSA STEFANIA SCIUTO
CIRCONFERENZE TANGENTI
DUE CIRCONFERENZE SI DICONO TANGENTI SE HANNO UN SOLO PUNTO IN COMUNE
CIRCONFERENZE TANGENTI ESTERNAMENTE
INDICHIAMO:
LA DISTANZA TRA I CENTRI DELLE DUE CIRCONFERENZE CON OO'
IL RAGGIO r DELLA CIRCONFERENZA C, CON OA
IL RAGGIO r’ DELLA CIRCONFERENZA C’, CON O’A’
POSSIAMO AFFERMARE CHE:
OO' = r + r'
DUE CIRCONFERENZE SONO TANGENTI ESTERNAMENTE SE
LA DISTANZA DEI LORO CENTRI È UGUALE ALLA SOMMA DEI
LORO RAGGI
CIRCONFERENZE TANGENTI INTERNAMENTE
INDICHIAMO:
LA DISTANZA TRA I CENTRI DELLE DUE CIRCONFERENZE CON OO'
IL RAGGIO r DELLA CIRCONFERENZA C, CON OA
IL RAGGIO r’ DELLA CIRCONFERENZA C’, CON O’A’
5
POSSIAMO AFFERMARE CHE:
OO' = r - r'
DUE CIRCONFERENZE SONO TANGENTI INTERNAMENTE SE
LA DISTANZA DEI LORO CENTRI È UGUALE ALLA DIFFERENZA
DEI LORO RAGGI
CIRCONFERENZE CONCENTRICHE
DUE CIRCONFERENZE SI DICONO CONCENTRICHE SE HANNO LO STESSO CENTRO
LA PARTE DI CERCHIO COMPRESA TRA DUE CIRCONFERENZE CONCENTRICHE SI CHIAMA
CORONA CIRCOLARE
SCHEDA DI SINTESI: CIRCONFERENZA E CERCHIO
ANGOLI AL CENTRO E ANGOLI ALLA CIRCONFERENZA
ALL’INTERNO DI UNA CIRCONFERENZA SI POSSONO DISEGNARE:
-
ANGOLI IL CUI VERTICE COINCIDE CON IL CENTRO DELLA CIRCONFERENZA
(ANGOLI AL CENTRO)
-
ANGOLI IL CUI VERTICE SI TROVA IN UN PUNTO QUALSIASI
DELLA CIRCONFERENZA (ANGOLI ALLA CIRCONFERENZA)
AD OGNI ANGOLO CORRISPONDE UN ARCO E NEL LINGUAGGIO SPECIFICO SI DICE CHE:
L’ANGOLO “INSISTE” SULL’ARCO
QUINDI, GUARDANDO LE FIGURE A FIANCO POSSIAMO DIRE CHE:
L’ANGOLO
L’ARCO
L’ANGOLO
L’ARCO
INSISTE SULL’ARCO
È L’ARCO CORRISPONDENTE DELL'ANGOLO AL CENTRO
INSISTE SULL’ARCO
È L’ARCO CORRISPONDENTE DELL'ANGOLO ALLA CIRCONFERENZA
PROF.SSA STEFANIA SCIUTO
SCHEDA DI SINTESI: CIRCONFERENZA E CERCHIO
PROF.SSA STEFANIA SCIUTO
ANGOLI AL CENTRO
L’ANGOLO AL CENTRO
È UN ANGOLO AVENTE IL VERTICE NEL CENTRO DI UNA CIRCONFERENZA
ESISTE UN SOLO ANGOLO AL CENTRO CHE INSISTE SU UN DATO ARCO.
OVVERO L ’ANGOLO AL CENTRO CHE HA IL VERTICE IN
O
ALL’ARCO
O E CHE CORRISPONDE
È SOLO UNO
DISEGNIAMO:
-
DUE ARCHI UGUALI
-
GLI ANGOLI AL CENTRO CHE INSISTONO SU TALI ARCHI:
E
E QUINDI
2 CORDE UGUALI AB E CD
E
OTTENIAMO 2 TRIANGOLI ISOSCELI CONGRUENTI PERCHÉ:
HANNO LE BASI CONGRUENTI AB
I LATI OBLIQUI CONGRUENTI AO = BO = DO = CO PERCHÉ SONO TUTTI RAGGI DELLA
= CD
CIRCONFERENZA
SE I TRIANGOLI SONO CONGRUENTI ALLORA ANCHE
=
POSSIAMO CONCLUDERE CHE:
ANGOLI AL CENTRO CHE INSISTONO SU ARCHI CONGRUENTI SONO TRA LORO CONGRUENTI.
ANGOLI ALLA CIRCONFERENZA
L’ANGOLO ALLA CIRCONFERENZA
È UN ANGOLO AVENTE IL VERTICE SULLA CIRCONFERENZA
P
CI SONO INFINITI ANGOLI ALLA CIRCONFERENZA CHE INSISTONO SU UN DATO ARCO E
HANNO TUTTI LA STESSA AMPIEZZA
CIOÈ:
SE DISEGNIAMO DIVERSI ANGOLI ALLA CIRCONFERENZA (VEDI DISEGNO A FIANCO) CHE
CORRISPONDONO TUTTI ALL’ARCO
, CI RENDIAMO CONTO CHE:
1.
POSSIAMO DISEGNARNE INFINITI
2.
HANNO TUTTI LA STESSA AMPIEZZA
SCHEDA DI SINTESI: CIRCONFERENZA E CERCHIO
PROF.SSA STEFANIA SCIUTO
RELAZIONE TRA ANGOLI AL CENTRO E ANGOLI ALLA CIRCONFERENZA
CONSIDERIAMO
UN ANGOLO AL CENTRO
UN ANGOLO ALLA CIRCONFERENZA
SE MISURIAMO I DUE ANGOLI NOTEREMO CHE
È IL DOPPIO DI
IN CONCLUSIONE:
P
OGNI ANGOLO ALLA CIRCONFERENZA È LA METÀ DELL'ANGOLO AL CENTRO CHE INSISTE SULLO STESSO ARCO.
CONSIDERIAMO
CHE INSISTE SULLA SEMICIRCONFERENZA (ARCO
UN ANGOLO AL CENTRO
E UN ANGOLO ALLA CIRCONFERENZA
SAPPIAMO CHE
)
CHE INSISTE SULLO STESSO ARCO
È IL DOPPIO DI
QUINDI:
POICHÉ
=180°SEGUE CHE
= 90°
DI CONSEGUENZA IL TRIANGOLO APB È UN TRIANGOLO RETTANGOLO CON L'IPOTENUSA CHE COINCIDE CON
IL DIAMETRO DELLA CIRCONFERENZA.
IN CONCLUSIONE:
UN TRIANGOLO INSCRITTO ALL’INTERNO DI UNA SEMICIRCONFERENZA È SEMPRE UN TRIANGOLO RETTANGOLO
CONSIDERIAMO
OP RELATIVA ALL'IPOTENUSA.
(RICORDIAMO CHE LA MEDIANA DI UN TRIANGOLO È IL
DEL LATO OPPOSTO)
LA MEDIANA
SEGMENTO CHE UNISCE UN VERTICE AL PUNTO MEDIO
NOTIAMO CHE
LA MEDIANA OP DEL TRIANGOLO NON È ALTRO CHE IL RAGGIO. DATO CHE L'IPOTENUSA DEL TRIANGOLO È
UGUALE AL DIAMETRO DELLA CIRCONFERENZA, POSSIAMO DIRE CHE LA MEDIANA È
.
LA META' DELL'IPOTENUSA
IN CONCLUSIONE:
.
NEL TRIANGOLO RETTANGOLO LA MEDIANA È LA META' DELL'IPOTENUSA
SCHEDA DI SINTESI: CIRCONFERENZA E CERCHIO
PROF.SSA STEFANIA SCIUTO
IL CERCHIO
IL CERCHIO È COSTITUITO DA TUTTI I PUNTI INTERNI
ALLA CIRCONFERENZA.
SETTORE CIRCOLARE
A
settore circolare
B
O
IL SETTORE CIRCOLARE È LA PARTE DI CERCHIO DELIMITATA DA:
-
DA UN ARCO
DAI DUE RAGGI
OA E OB
SEGMENTO CIRCOLARE
SEGMENTO CIRCOLARE A UNA BASE
IL SEGMENTO CIRCOLARE A UNA BASE
È LA PARTE DI CERCHIO COMPRESA TRA UNA CORDA E UN ARCO
SE LA CORDA CHE DISEGNIAMO È IL DIAMETRO, IL CERCHIO RISULTA DIVISO IN DUE PARTI
UGUALI OGNUNA DELLE QUALI SI CHIAMA SEMICERCHIO:
SEGMENTO CIRCOLARE A DUE BASI
IL SEGMENTO CIRCOLARE A DUE BASI
È LA PARTE DI CERCHIO COMPRESA TRA LE DUE CORDE PARALLELE
SCHEDA DI SINTESI: CIRCONFERENZA E CERCHIO
PROF.SSA STEFANIA SCIUTO
LUNGHEZZA DELLA CIRCONFERENZA E AREA DEL CERCHIO
LUNGHEZZA DELLA CIRCONFERENZA
c = d OPPURE c = 2r
FORMULE INVERSE:
RAGGIO r
c
2
DIAMETRO: d
c
AREA DEL CERCHIO
A = r2π
FORMULA INVERSA:
RAGGIO
r
A
SCHEDA DI SINTESI: CIRCONFERENZA E CERCHIO
PROF.SSA STEFANIA SCIUTO
LUNGHEZZA DI UN ARCO DI CIRCONFERENZA
α
360°
C : lunghezza della circonferenza
REGOLA
TRA UN ANGOLO AL CENTRO L’ARCO CORRISPONDENTE ESISTE UNA RELAZIONE DI
PROPORZIONALITÀ DIRETTA
PROPORZIONE
LA PROPORZIONE CHE LEGA QUESTE GRANDEZZE È LA SEGUENTE
l : C = α : 360
FORMULE
l =Cxα
360
C = l x 360
α
α = l x 360
c
SCHEDA DI SINTESI: CIRCONFERENZA E CERCHIO
PROF.SSA STEFANIA SCIUTO
AREA DEL SETTORE CIRCOLARE
α
360°
REGOLA
TRA UN ANGOLO AL CENTRO L’AREA DEL SETTORE CIRCOLARE ESISTE UNA RELAZIONE DI
PROPORZIONALITÀ DIRETTA
PROPORZIONE
LA PROPORZIONE CHE LEGA QUESTE GRANDEZZE È LA SEGUENTE
As: Ac = α : 360
FORMULE
As = Ac x α
360
Ac = As x 360
α
α = As x 360
Ac












