Il Primo Principio della Termodinamica
Si consideri un Sistema termodinamico qualsiasi (un sistema (P,v,T) consente un
controllo più agevole dello stato macroscopico, ma non è essenziale ai fini della
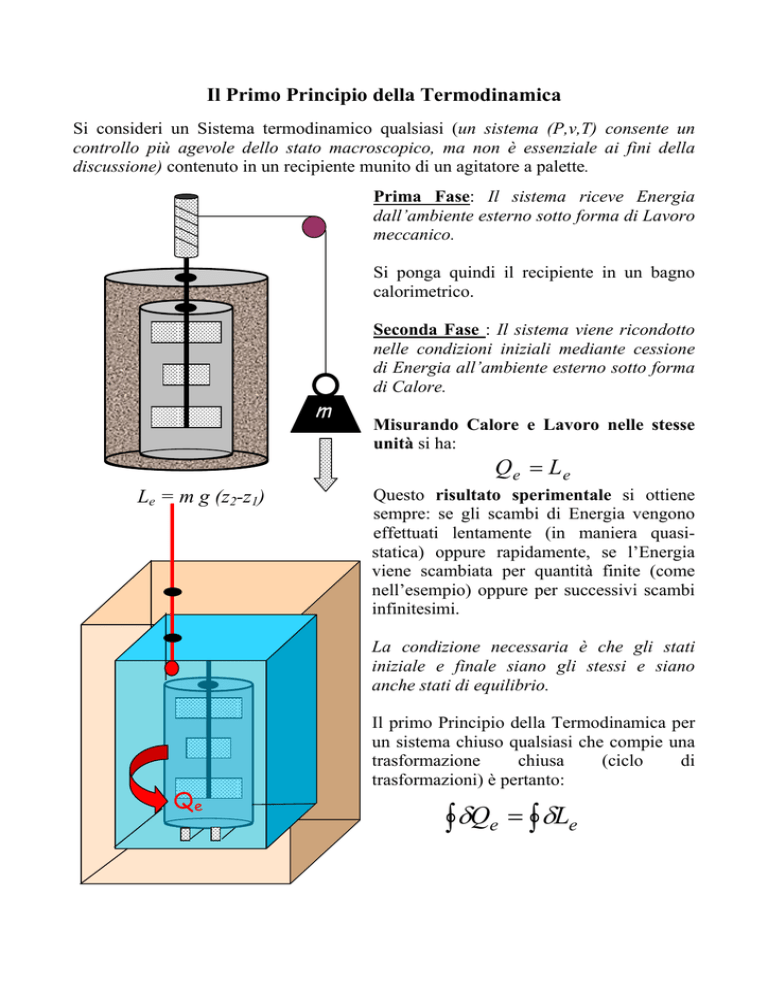
discussione) contenuto in un recipiente munito di un agitatore a palette.
Prima Fase: Il sistema riceve Energia
dall’ambiente esterno sotto forma di Lavoro
meccanico.
Si ponga quindi il recipiente in un bagno
calorimetrico.
m
Seconda Fase : Il sistema viene ricondotto
nelle condizioni iniziali mediante cessione
di Energia all’ambiente esterno sotto forma
di Calore.
Misurando Calore e Lavoro nelle stesse
unità si ha:
Qe = Le
Le = m g (z2-z1)
Questo risultato sperimentale si ottiene
sempre: se gli scambi di Energia vengono
effettuati lentamente (in maniera quasistatica) oppure rapidamente, se l’Energia
viene scambiata per quantità finite (come
nell’esempio) oppure per successivi scambi
infinitesimi.
La condizione necessaria è che gli stati
iniziale e finale siano gli stessi e siano
anche stati di equilibrio.
Qe
Il primo Principio della Termodinamica per
un sistema chiuso qualsiasi che compie una
trasformazione
chiusa
(ciclo
di
trasformazioni) è pertanto:
∫ δQe = ∫ δLe
Schema originale dell’apparato sperimentale usato da Joule
Foto dell’apparato sperimentale usato da Joule
La figura mostra un sistema impegnato in un ciclo chiuso di trasformazioni; ancora
una volta si vuole sottolineare che si è scelto un sistema (P,v,T) solo perché le sue
trasformazioni sono facilmente rappresentabili sul piano di Clapeyron.
2
1
2
1
1( A )
2( B )
1( A )
2( B )
∫ δQ + ∫ δQ = ∫ δL + ∫ δL
P
1
B
2
2
1( A )
1( B )
∫ (δQ − δL ) = ∫ (δQ − δL ) = ......
A
2
v
2
∫ (δ Q − δ L ) = ∆E = E 2 − E1
1
La somma algebrica tra le diverse forme di Energia scambiate dal sistema con
l’esterno è una funzione di stato e rappresenta la variazione di Energia Interna del
sistema.
Dal punto di vista macroscopico l’Energia Interna viene introdotta (ne viene postulata
l’esistenza) come quella forma di Energia necessaria a garantire il Principio di
Conservazione dell’Energia in un sistema isolato, dove si ha infatti:
Qe = 0
Le = 0
E = cos t
∫ dE = 0
essendo l’Energia Interna una funzione di stato.
Nel caso particolare di un sistema fermo, alla quota di riferimento, inerte dal punto di
vista chimico e nucleare si ha:
Qe = ∆U + Le
E ≡U
δQ = dU + δL
Primo Principio della Termodinamica per un sistema chiuso qualsiasi che compie una
trasformazione aperta.
Per un sistema (P,v,t), che può scambiare lavoro con l’esterno sotto l’unica forma di
lavoro di espansione/compressione si ha ancora:
2
Qe = ∆U + ∫ Pdv ; δQ = dU + Pdv ( 1kg )
1
Energia Interna di un sistema (P,v,T).
Un primo tentativo di correlare l’Energia Interna di un sistema (P,v,T) alle
caratteristiche macroscopiche che identificano lo stato del sistema, fu condotto da
James Prescott Joule nel 1847.
1
2
Due robusti recipienti di forma sferica sono connessi tra loro mediante un tubo
munito di rubinetto. Nel recipiente 1 è contenuta una certa quantità di gas, mentre nel
recipiente 2 è stato fatto il vuoto.
I due recipienti sono immersi in un bagno calorimetrico che a sua volta è posto in un
contenitore termicamente isolante.
Le linee tratteggiate identificano i contorni del sistema che comprende i due
recipienti ed il tubo di comunicazione.
L’esperienza veniva condotta aprendo bruscamente il rubinetto ed osservando la
variazione di temperatura del bagno calorimetrico.
Lavorando con piccole quantità di gas leggeri, Joule osservò che l’espansione libera
(verso uno spazio vuoto) di un gas rarefatto non produce nessuna variazione
osservabile della temperatura del bagno calorimetrico, cosa che sta a dimostrare
che non vi è stato trasferimento di Energia sotto forma di calore tra il sistema e
l’esterno.
Si noti che il sistema (P,v,T), chiuso nelle pareti rigide dei due contenitori, non può
scambiare Energia con l’esterno sotto forma di Lavoro di espansione.
Si ha quindi:
Qe = 0 (osservazione sperimentale)
Le = 0 (scelta dei contorni del sistema)
Segue dal Primo Principio:
∆U = 0
Relazione originale di Joule sull’apparecchiatura usata per l’espansione libera
Foto dell’apparato sperimentale usato da Joule
Considerando che è:
U = U ( T ,v )
;
⎛ ∂U ⎞
⎛ ∂U ⎞
dU = ⎜
⎟ dv
⎟ dT + ⎜
∂
v
∂
T
⎝
⎠T
⎝
⎠v
dall’esperienza ricaviamo dU = dT = 0 ma certamente il volume del gas è cambiato,
quindi dv ≠ 0 se ne deduce:
⎛ ∂U ⎞
⎜
⎟ =0
⎝ ∂v ⎠T
Che può leggersi: l’Energia Interna di un sistema (P,v,T) non è funzione del volume
se lavoriamo a Temperatura costante .
Ma è anche:
U = U(T , p )
;
⎛ ∂U ⎞
⎛ ∂U ⎞
dU = ⎜
⎟ dT + ⎜
⎟ dP
∂
∂
T
P
⎝
⎠P
⎝
⎠T
e poiché anche la pressione del gas è cambiata:
⎛ ∂U ⎞
⎜
⎟ =0
⎝ ∂P ⎠T
Che può leggersi: l’Energia Interna di un sistema (P,v,T) non è funzione della
pressione se lavoriamo a Temperatura costante .
Si conclude quindi che l’Energia Interna di un sistema (P,v,T) è funzione soltanto
della Temperatura.
U = f(T)
sistema (P,v,T)
Numerose critiche possono essere portate alle evidenze sperimentali ricavabili
dall’esperienza di Joule. Cercheremo quindi di verificarne i risultati facendo ricorso
alla teoria cinetica dei gas.
E’ noto che il concetto di Temperatura di un gas è legato all’agitazione delle sue
molecole, abbiamo infatti introdotto questa grandezza fisica come funzione
dell’Energia Cinetica Media delle molecole.
f
Come è stato dimostrato nel corso di Fisica: E cin = kT
2
Essendo f i gradi di libertà della molecola (3 = monoatomico, 5 = biatomico, 6
triatomico,….) e k = R/Nav la costante di Boltzmann data dal rapporto tra la costante
dei gas ed il numero di Avogadro.
3
=
kT chiuso in un recipiente a
E
cin
Si consideri un gas reale monoatomico
2
pareti rigide separato, mediante un setto rimovibile, da un volume in cui regni il
vuoto.
Mettendo in bruscamente in comunicazione le due camere mediante rottura del setto,
l’Energia interna del gas non può cambiare perché il sistema è supposto isolato
(meccanicamente e termicamente).
Poiché l’Energia Interna del gas reale è composta da una parte cinetica e da una parte
potenziale (U = Ecin + Epot) all’aprirsi del setto può solo avere luogo una
ridistribuzione dell’Energia U tra le due componenti.
In particolare, poiché le molecole del gas trovano un spazio maggiore in cui muoversi
(aumento delle distanze intermolecolari) la parte Potenziale dell’Energia Interna
aumenta a scapito di quella Cinetica, con conseguente diminuzione della
Temperatura del gas.
Soltanto nell’ipotesi che la parte Potenziale fosse trascurabile rispetto alla
componente Cinetica (U ≡ Ecin) la Temperatura del gas non cambierebbe.
Pertanto, per un gas composto da molecole piccolissime e assai distanti, detto anche
“gas di Energia Cinetica” valgono le relazioni:
⎛ ∂U ⎞
⎜
⎟ =0
⎝ ∂v ⎠T
⎛ ∂U ⎞
⎜
⎟ =0
∂
P
⎝
⎠T
Che costituiscono un’altra definizione del “gas perfetto”.
CALORI SPECIFICI
Quando un sistema di massa (o peso) m scambia una certa quantità di calore Qe con l’esterno, la sua
temperatura può aumentare, diminuire o restare invariata.
Si definisce Capacità termica media:
⎛Q ⎞
C pm = ⎜ e ⎟
⎝ ∆T ⎠Trasf
Se il sistema ha peso o massa unitaria e la quantità di calore scambiata è infinitesima, si definisce
Calore specifico lungo la trasformazione x
⎛ δQ ⎞
cx = ⎜
⎟
⎝ dT ⎠Trasf x
(1 kg)
Ricordando che in una trasformazione isocora di un sistema p,v,T (1 kg) si ha:
δQ = dU + pdv
e
(δQ )v = dU
Si può scrivere:
⎛ ∂U ⎞
⎛ ∂U ⎞
dU = ⎜
⎟ dT + ⎜
⎟ dv ;
⎝ ∂T ⎠ v
⎝ ∂v ⎠ T
⎛ δQ ⎞
⎛ ∂U ⎞
dU = ⎜
⎟ dT + ⎜
⎟ dv ;
⎝ ∂T ⎠ v
⎝ ∂v ⎠ T
⎛ ∂U ⎞
dU = c v dT + ⎜
⎟ dv
⎝ ∂v ⎠ T
L’ultima relazione è valida sempre per un sistema (p,v,T).
Per un 1 kg di gas perfetto:
poiché si è dimostrato che la U non è funzione del volume lavorando a temperatura costante, si ha
sempre:
dU = cv dT
che esprime la relazione funzionale tra la Energia interna di un gas perfetto ed i parametri di stato.
Confrontando la relazione valida sempre per un sistema p,v,T e quella valida sempre per un gas
perfetto, si nota che la prima è composta da due termini, il primo dei quali può essere visto come il
comportamento ideale del gas ed il secondo come la deviazione del gas reale dal comportamento
ideale.
Dovendo essere U = f(T) soltanto, è evidente che anche cv = f(T) soltanto.
Il Primo Principio della termodinamica per un sistema chiuso (p,v,T) composto da 1 kg di gas
perfetto si scriverà:
δQ = c v dT + pdv
Differenziando la relazione di stato di un gas perfetto nella forma pv = R’T (1kg) ed utilizzando il
I° Principio si ha:
pdv + vdp = R’dT
δQ = cv dT + R’dT – vdp
δQ = (cv + R’)dT – vdp
In una trasformazione isobara si avrà :
(δQ)p = (cv + R’)dT – vdp
⎛ δQ ⎞
⎟ = c p è, per definizione, il calore specifico a pressione costante, dalla relazione
⎝ dT ⎠ p
precedente si ricava la relazione di Mayer tra i calori specifici fondamentali cp e cv :
E poiché ⎜
R’ = (cp - cv)
R’ = R/Mol è una costante (per il particolare gas preso in considerazione), ed essendo cv = f(T)
soltanto, anche cp = f(T) soltanto, ed anche il loro rapporto k = cp/cv , che è evidentemente > 1
(essendo R’ > 0 e quindi cp > cv). Approfondiremo più avanti il significato fisico del termine k.
In alcune precedenti occasioni abbiamo definito un gas perfetto come un “gas di Energia Cinetica”.
Questa definizione nasce dalla considerazione che le particelle (atomi o molecole) che lo
compongono sono talmente piccole e distanti tra loro che le forme di Energia diverse da quella
cinetica (e cioè quelle potenziale, rotazionale e vibrazionale) sono talmente piccole da potersi
ritenere trascurabili o nulle.
Pertanto l’Energia Interna di un gas perfetto formato da N particelle può scriversi:
N
U = ∑ E cin = N E cin
con
1
E cin =
f
kT
2
ek=
R
N Av
dove termine f rappresenta i “gradi di libertà del sistema”.
Gradi di libertà di un sistema meccanico.
Il principio di equipartizione dell’Energia afferma che in un gas l’energia cinetica media di una
molecola si distribuisce ugualmente tra i suoi diversi gradi di libertà.
z
z
z
y
x
Atomo
y
yd
x
Molecola biatomica
x
In meccanica, f è il numero di quantità necessarie per determinare la configurazione di un oggetto
meccanico o di un sistema ossia il numero minimo dei parametri geometrici necessari a individuare
la posizione delle parti che compongono il sistema.
Un gas monoatomico possiede allora tre gradi di libertà perché in un sistema di assi cartesiani basta
conoscere le sue tre coordinate perché sia individuata la sua posizione.
Una molecola biatomica rigida (in cui si suppone che la distanza d tra gli atomi non possa variare e
quindi trascurando l’energia associata a moti di vibrazione lungo l’asse che idealmente congiunge i
due nuclei) ha 5 gradi di libertà: infatti a una data posizione della molecola corrispondono le 6
coordinate cartesiane dei due atomi che sono però legate dalla condizione di rigidità che fissa la
distanza tra i due atomi. Ne risulta che il numero minimo di coordinate da conoscere è 6 − 1 = 5.
Se consideriamo una molecola che ha tre atomi rigidamente collegati tra loro, è ovvio che ad una
data posizione della molecola corrispondono 9 coordinate cartesiane, esse però sono legate da tre
condizioni di rigidità, quindi il numero di gradi di libertà è 9 − 3 = 6.
z
z
y
y
d1 z
x d
x
3
y
d2
x
Molecola triatomica
L'aggiunta di un quarto atomo rigidamente collegato agli altri tre comporta l'aumento di 3
coordinate, ma anche l'introduzione di 3 nuove condizioni di rigidità quindi il numero di gradi di
libertà rimane 6. Ciò è vero per un qualunque numero di atomi e quindi anche per un sistema rigido
continuo.
Vogliamo fare osservare che la scelta delle coordinate cartesiane per individuare la posizione della
molecola non è l'unica possibile: in alcuni casi può essere preferibile utilizzare altri tipi di
coordinate. Per esempio, nel caso di una molecola biatomica rigida si possono scegliere le tre
coordinate cartesiane del centro di massa della molecola e i due angoli che individuano la
direzione della congiungente i due atomi rispetto agli assi coordinati.
Molecola biatomica
L’Energia Interna di 1 Mole di Gas Perfetto sarà allora:
U = N Av
f R
T
2 N Av
=
f
RT
2
avremo quindi:
f
⎛ ∂U ⎞
Cv Mol = ⎜
⎟ = R
⎝ ∂T ⎠ v 2
Cp Mol = Cv Mol + R
=
2+f
R
2
Pertanto: Assumendo come valido il modello a legami rigidi, i calori molari fondamentali dei
Gas Perfetti non dipendono dalla Temperatura, ma sono costanti.
E facile calcolare i valori dei Calori Molari per le diverse famiglie di gas perfetti (mono- bi- triatomici, ecc); da questi valori si possono ricavare quelli dei calori specifici dei diversi gas perfetti
dividendo il corrispondente Calore Molare per il peso molecolare.
Gas Perfetto monoatomico f = 3
Cv Mol =
3
R
2
⎡ kcal ⎤
= 2,98 ⎢
⎥
⎣ Mol °C ⎦
Cp Mol =
5
R
2
= 4,97
k=
Cp Mol
Cv Mol
⎡ kcal ⎤
⎢ Mol °C ⎥
⎣
⎦
= 1,666
Gas Perfetto biatomico (molecola rigida) f = 5
⎡ kcal ⎤
⎢ Mol °C ⎥
⎣
⎦
Cv Mol =
5
R
2
= 4,97
Cp Mol =
7
R
2
⎡ kcal ⎤
= 6,95 ⎢
⎥
⎣ Mol °C ⎦
k=
Cp Mol
Cv Mol
= 1,40
Gas Perfetto triatomico (molecola rigida) f = 6
Cv Mol =
6
R
2
⎡ kcal ⎤
= 5,96 ⎢
⎥
⎣ Mol °C ⎦
Cp Mol =
8
R
2
⎡ kcal ⎤
= 7,95 ⎢
⎥
⎣ Mol °C ⎦
k=
Cp Mol
Cv Mol
= 1,33
La tabella riporta i valori sperimentali dei Calori Molari a volume costante e del rapporto Cp/Cv
(qui indicato con γobs) per alcuni gas; i valori sono riferiti alle condizioni di temperatura e pressione
indicate, ma, almeno per i gas monoatomici, essi possono ritenersi validi in un ambito molto vasto
di valori di temperatura e pressione.
L’ultima colonna riporta i valori fittizi del numero di gradi di libertà reff che possono calcolarsi con
f
la formula Cv Mol = R , utilizzando i valori sperimentali del Calore Molare CvMol.
2
Come è evidente, in molti casi il numero di gradi di libertà non è espresso da un numero intero, ciò
avviene quando l’energia interna della molecola non è tutta legata alla sua energia cinetica ma è
distribuita tra l’energia di traslazione e quelle di rotazione e vibrazione dei componenti della
molecola stessa.
Nel caso dei gas monoatomici, che corrispondono quasi perfettamente al modello che ci siamo
costruiti, tutta l’Energia interna è cinetica ed il numero dei gradi di libertà corrisponde esattamente a
quanto previsto dal nostro modello.
Nel caso di molecole più complesse, il modello “a manubrio rigido” non è più applicabile, tanto più
quanto la temperatura (e quindi l’energia in gioco) tende ad aumentare.
Nella figura è rappresentato il caso della molecola biatomica dell’Azoto che a basse temperature
esibisce un numero di gradi di libertà reff pari al valore di 5 previsto dal nostro modello a legami
rigidi. All’aumentare della temperatura una quota parte sempre più grande dell’Energia meccanica
della molecola viene impegnata dai moti di rotazione e vibrazione. Questo fatto si riflette in un
aumento del Calore Molare a Volume costante e quindi in un aumento del valore fittizio dei gradi
di libertà reff
Riprendiamo in considerazione le ipotesi che abbiamo posto alla base della definizione di gas
perfetto : secondo il nostro modello le particelle che compongono il gas sono puntiformi e pertanto
l’energia meccanica da loro posseduta può essere soltanto di tipo cinetico ed i gradi di libertà
corrispondenti a questa situazione non possono essere più di 3.
E’ evidente che solo un gas monoatomico fornisce una ottima approssimazione al nostro modello
teorico e può essere considerato un “gas di energia cinetica” o, secondo la definizione di alcuni
Autori, un “gas piùcheperfetto”.
I calori molari (e quindi quelli specifici) a volume costante ed a pressione costante di un gas
monatomico sono evidentemente costanti e pari rispettivamente a 3/2R e 5/2R come abbiamo
dimostrato sopra.
Volendo estendere il nostro modello di gas perfetto a gas con due o più atomi nella loro molecola
dobbiamo prendere in considerazione il fatto che l’aumento della Temperatura “attiva” altri gradi di
libertà della molecola provocando un aumento dei valori dei calori molari.
Nell’esempio riportato in figura la molecola biatomica dell’Azoto esibisce a bassa temperatura i 5
gradi di libertà previsti dal legame rigido tra i due atomi, poi, con l’aumentare della temperatura,
l’Energia meccanica si distribuisce anche nei moti di rotazione e vibrazione portando fino a 7 i
gradi di libertà della molecola, con conseguente aumento del valore dei calori molari.
Pertanto possiamo ritenere che, a parte il caso dei gas monoatomici, ove non si consideri valido il
modello a legami rigidi, i calori molari (e quindi quelli specifici) di un gas perfetto poliatomico
siano funzioni (crescenti) della temperatura.
In questo corso faremo riferimento al modello cinetico di gas perfetto e considereremo pertanto
costanti i gradi di libertà dei gas perfetti che utilizzeremo nelle dimostrazioni (gas monoatomico :
f = 3; gas biatomico : f = 5, gas triatomico : f = 6) e costanti i valori dei loro calori specifici e
molari.
Processi a Pressione costante – Entalpia.
Nelle prime lezioni di questo corso abbiamo dimostrato che il Calore non è una funzione di stato
perché la quantità di calore scambiata da un sistema dipende dalla trasformazione seguita dal
sistema stesso per assecondare i vincoli posti dall’ambiente esterno.
E’ però evidente che, fissata una trasformazione (p.es. a p = cost, T = cost, o secondo un qualunque
altro cammino in cui siano stati assegnati punto per punto precisi valori di p,v,T ) il calore
scambiato lungo la trasformazione è una funzione dello stato in cui si è portato il sistema.
Lungo una trasformazione assegnata, il calore è una funzione di stato.
Questa proprietà si rivela particolarmente utile nello studio dei processi che avvengono più
comunemente nella pratica della termotecnica civile o industriale.
Abbiamo già visto che, nei processi a volume costante di un sistema (p,v,T) qualsiasi, il Calore
scambiato è pari alla variazione di Energia Interna e può essere calcolato come differenza di
Energia Interna tra gli stati iniziale e finale della trasformazione.
Altri processi assai utilizzati nella pratica sono quelli che avvengono a Pressione costante, (p.es. il
riscaldamento di un liquido in aria libera a pressione atmosferica o i processi che avvengono
all’interno degli scambiatori di calore), anche in questo caso il calore scambiato può essere valutato
dagli stati iniziale e finale della trasformazione per mezzo di una nuova funzione di stato.
Definiamo Entalpia :
J = U + pv
Essa è evidentemente una funzione di stato perché si è ottenuta dalla combinazione di una funzione
di stato con il prodotto di due variabili di stato.
E’ ovvio che qualunque combinazione (lineare o no) di funzioni e variabili di stato è essa stessa
una funzione di stato, vi è però il vincolo della omogeneità; in questo caso infatti i due termini che
compongono l’Entalpia sono omogenei ad una Energia.
Ricordando il primo Principio per un sistema p,v,T (1 kg)
δQ = dU + pdv ; differenziando il prodotto pv si ha : d(pv) = vdp + pdv ; pdv = d(pv) – vdp
δQ = d(U + pv) – vdp ; δQ = dJ – vdp
In un processo a pressione si costante si ha dunque:
(δQ)p = dJ
Ed anche:
⎛ δQ ⎞ ⎛ ∂J ⎞
cp = ⎜
⎟ =⎜ ⎟
⎝ dT ⎠ p ⎝ ∂T ⎠ p
Essendo l’Entalpia una funzione di stato potrò scrivere:
⎛ ∂J ⎞
⎛ ∂J ⎞
dJ = ⎜ ⎟ dT + ⎜⎜ ⎟⎟ dp
⎝ ∂T ⎠ p
⎝ ∂p ⎠ T
=
⎛ ∂J ⎞
c p dT + ⎜⎜ ⎟⎟ dp
⎝ ∂p ⎠ T
In particolare, per un gas perfetto può scriversi:
J = U + pv = U + R’T ; dJ = dU + R’dT = cvdT + R’dT = (cv + R’)dT = cpdT
Pertanto per un gas perfetto, essendo cp = cost si ha che, per qualsiasi trasformazione :
dJ = cpdT [J = f(T) solo]
⎛ ∂J ⎞
⎛ ∂J ⎞
Dall’espressione generale si ricava poi : ⎜⎜ ⎟⎟ = 0 ed anche : ⎜ ⎟ = 0
⎝ ∂v ⎠ T
⎝ ∂p ⎠ T
Energia Interna
Entalpia
⎛ dU ⎞
dU = c v dT + ⎜
⎟ dv
⎝ dv ⎠ T
⎛ dJ ⎞
dJ = c p dT + ⎜⎜ ⎟⎟ dp
⎝ dp ⎠ T
[dU = c v dT ]v=cos t
dU = c v dT (gas perfetto)
[dJ = c dT]
p
p =cos t
dJ = c p dT (gas perfetto)
CALORI SPECIFICI DEI GAS PERFETTI
Come si è detto in precedenza, ad ogni trasformazione può essere associato un calore specifico:
⎛ δQ ⎞
cx = ⎜
⎟
⎝ dT ⎠Trasf x
(1 kg)
Pertanto, scelto un punto A (P,v,T) sul piano di Clapeyron, si possono definire infiniti calori
specifici in corrispondenza alle infinite trasformazioni che possono portare dallo stato A ad un altro
stato B avente una temperatura T’ = T ± dT
Trasformazione Isoterma:
Partendo dal punto A si raggiunge l’isoterma T+dT proseguendo su T all’infinito verso destra o
verso sinistra.
p
⎛ δQ ⎞
cT = ⎜
⎟ =±∞
⎝ dT ⎠T
Le
δQ = c v dT + pdv
(cT = - ∞)
(δQ) T = δL
A
-L
(cT = + ∞)
+L
T+dT
T
T
Qe
v
Trasformazione Isobarica
p
Le
⎛ δQ ⎞
cp = ⎜
⎟
⎝ dT ⎠ p
δQ = c v dT + pdv
A
(cp)
P
(δQ) p = dJ
B T+dT
Qe
T
v
Trasformazione Isocora
p
⎛ δQ ⎞
cv = ⎜
⎟
⎝ dT ⎠ v
B
δQ = c v dT + pdv
(cv)
(δQ) v = dU
T+dT
A
Qe
T
v
E’ facile vedere che, per un gas perfetto, è sempre cp > cv , infatti per uno stesso salto di
temperatura dT si ha :
(δQ)p = dU + δL
||
(δQ)v = dU
da cui (δQ)p > (δQ)v perché il calore fornito a pressione costante deve servire anche a produrre
Lavoro.
E’ evidente che ogni successione continua di stati di (P,v,T) di equilibrio rappresenta una possibile
trasformazione quasi-statica di una sostanza; la difficoltà sta però nel tradurre questa successione
di stati in una espressione analitica del tipo X=f(Y,Z) che possa consentire di trovare le proprietà
termodinamiche della trasformazione mediante le regole di derivazione o integrazione.
n
Una forma analitica assai semplice è quella detta “politropica” pv = cost (con n = costante).
La forma politropica è una relazione molto versatile, infatti quasi tutte le trasformazioni di più largo
impiego nella pratica possono essere messe sotto forma politropica e inoltre, come vedremo più
avanti, dati due punti nello spazio (p,v,T), è sempre possibile trovare una trasformazione politropica
che colleghi i due stati.
n=0)
pv0 = cost
≡
p = cost (isobara)
n=1)
pv1 = cost
≡
T = cost (isoterma)
≡
v = cost (isocora)
n=∞) p1/nv = cost’
n=k)
pvk = cost
con k = cp/cv
(adiabatica)
Quest’ultima trasformazione riveste particolare importanza perché dimostreremo in seguito che un
sistema composto da un gas perfetto che segue una successione di stati equilibrio interno durante i
quali si ha sempre pvk = cost, non scambia calore con l’esterno.
Trasformazione Politropica Adiabatica
Le
p
⎛ δQ ⎞
ck = ⎜
⎟ =0
⎝ dT ⎠ k
B
(ck)
0 = c v dT + pdv
A
T+dT
dU = − δL
T
v
Trasformazione Politropica (generica)
Le
p
B
⎛ δQ ⎞
cn = ⎜
⎟ = cos t
⎝ dT ⎠ n
(cn)
δQ = c v dT + pdv
T+dT
A
Qe
T
v
Per un sistema P,v,T che segue una politropica pvn = cost = B qualsiasi, è facile calcolare il lavoro
scambiato dal sistema con l’esterno:
L12
[
]
[
]
[
B
B
pv n 1− n
1
1− n
1− n
= ∫ pdv = ∫ n dv =
v 2 − v1 =
v 2 − v11− n =
p1v1 − p 2 v 2
1− n
1− n
n −1
1
1v
2
2
]
che può anche mettersi nelle forme seguenti, che tornano più comode qualora, come spesso avviene,
siano note tutte le caratteristiche del punto di partenza (1) ed una sola delle caratteristiche del punto
finale (2).
L12
n −1
p1v1 ⎡ ⎛ v1 ⎞ ⎤
⎢1 − ⎜ ⎟ ⎥
=
n − 1 ⎢ ⎜⎝ v 2 ⎟⎠ ⎥
⎦
⎣
oppure
n −1 ⎤
⎡
p1v1 ⎢ ⎛ p 2 ⎞ n ⎥
1− ⎜ ⎟
n − 1 ⎢ ⎜⎝ p1 ⎟⎠ ⎥
⎢⎣
⎥⎦
Si osservi che, nel caso della politropica isoterma, la soluzione dell’integrale è formalmente diversa:
⎛v ⎞
⎛p ⎞
= p1v1 ln ⎜⎜ 2 ⎟⎟ = p1v1 ln ⎜⎜ 1 ⎟⎟
v
⎝ v1 ⎠
⎝ p2 ⎠
2 dv
L12 = B ∫
1
Utilizzando l’equazione dei gas perfetti è possibile scrivere la forma politropica in funzione dei
parametri di stato p,v,T nei seguenti modi:
pv =C ;
n
Tv
T
n −1
1− n
p n
p1 ⎛ v 2 ⎞
=⎜ ⎟
p 2 ⎜⎝ v1 ⎟⎠
n
n −1
=C ;
T1 ⎛ v 2 ⎞
=⎜ ⎟
T2 ⎜⎝ v1 ⎟⎠
=C ;
T1 ⎛ p 2 ⎞
=⎜ ⎟
T2 ⎜⎝ p1 ⎟⎠
1− n
n
E’ interessante osservare che qualunque trasformazione di un gas perfetto durante la quale il calore
specifico cn sia costante può essere messa sotto forma politropica, si ha infatti:
δQ = c n dT = c v dT + pdv ; (c n − c v )dT = pdv
α pdv + β vdp = 0
⎛ pdv + vdp ⎞
(c n − c v )⎜
⎟ = pdv
R'
⎝
⎠
con α e β cos tan ti, dividendo per pv si ha : α
int egrando : p β v α = cos t ; pv n = cos t '
dv
dp
+β = 0
v
p
Riepilogo delle trasformazioni dei gas perfetti
- Trasformazione Isocora
Definizione
:
v = costante
;
dv =0
I° Principio
:
δQ = cv dT + pdv
Calore
:
Q = U 2 − U1 = c v (T2 − T1 ) = c v
∆U
:
cv (T2 - T1)
Lavoro
:
0
v
(p 2 − p1 )
R'
- Trasformazione Isobara
Definizione
:
p = costante
;
dp =0
I° Principio
:
δQ = cv dT + pdv = dJ = cp dT
Calore
:
∆J = c p (T2 − T1 ) = c p
∆U
:
cv (T2 - T1) = cv (v2 - v1) p/R’
Lavoro
:
p
(v 2 − v1 )
R'
2
∫ pdv = p (v2 - v1) = R’(T2 - T1)
1
- Trasformazione Isoterma (Isodinamica)
Definizione
:
T = costante ;
I° Principio
:
δQ = cv dT + pdv
Calore
=
Lavoro
∆U
:
0
Lavoro
:
2
2 dv
1
1
∫ pdv = R ' T ∫
v
dT =0
= R’T ln(v2/v1) = R’T ln(p1/p2)
- Trasformazione Politropica
Definizione
:
pvn = costante (con n = costante);
I° Principio
:
δQ = cv dT + pdv
Calore
:
Q = c v (T2 − T1 ) +
∆U
:
cv (T2 - T1)
Lavoro
:
1
(p1v1 − p 2 v 2 ) = R ' (T1 − T2 )
n −1
n −1
R'
(T1 − T2 ) = ⎛⎜ c v − R ' ⎞⎟(T2 − T1 )
n −1
n −1 ⎠
⎝
Dall’espressione del calore scambiato lungo una generica politropica di indice n si ha poi:
cp
R' ⎞
⎛ δQ ⎞
⎛
⎜
⎟ = cn = ⎜ cv −
⎟ ed essendo : R ' = (c p − c v ) e k =
n −1 ⎠
cv
⎝ dT ⎠ n
⎝
si ha :
⎛n−k⎞
cn = cv ⎜
⎟ = cos t
⎝ n −1 ⎠
- Trasformazione Politropica Adiabatica
Definizione
:
pvk = costante (con k = cp/cv);
I° Principio
:
δQ = cv dT + pdv
Calore
:
= 0 essendo n = k
∆U
:
cv (T2 - T1) = - L12
Lavoro
:
1
(p1v1 − p 2 v 2 ) = R ' (T1 − T2 )
k −1
k −1
⎛n−k⎞
ck = cv ⎜
⎟=0
⎝ n −1 ⎠
Riepilogo delle trasformazioni politropiche sul piano di Clapeyron
p
Nel diagramma sono rappresentate le
principali trasformazioni politropiche
che possono essere realizzate mediante
riscaldamento da un generico punto A a
temperatura T ad un generico punto
appartenente all’isoterma T+dT ed i
relativi valori dei calori specifici.
(ck=0)
(cn<k)
(c<0)
(cn>k)
(c>0)
(cT -∞)
(cv)
(cp)
A
(cT +∞)
T+dT
T
v
Osserviamo
in
particolare
le
trasformazioni che appartengono all’arco
tratteggiato in verde, esse hanno tutte
calori specifici positivi che esibiscono
valori decrescenti tra +∞ e 0:
Calore specifico +∞
= espansione isoterma
indice n = 1
Calore specifico cp>0
= espansione isobara
indice n = 0
Calore specifico cv>0
= riscaldamento isocoro
indice n = +∞ [cp>cv]
= compressione politropica indice k < n < +∞
Calore specifico cn>k>0
Le politropiche di riscaldamento per compressione aventi indice compreso tra +∞ e k (tra l’isocora
e l’adiabatica) hanno ancora calore specifico positivo, come è facile dimostrare considerando che il
lavoro fornito dall’esterno durante la compressione è (dalle aree sottese) evidentemente inferiore a
quello fornito per realizzare la compressione adiabatica. Per ottenere la stessa temperatura raggiunta
nella compressione adiabatica sarà pertanto necessario aggiungere una certa quantità di calore
(entrante = positivo). Pertanto cn = (δQ/dT) > 0
dU = - δLk
||
∨ (in valore assoluto)
dU = - δLn>k + δQ
Calore specifico ck = 0
Calore specifico cn>k>0
= compressione adiabatica indice k
= compressione politropica indice 1< n < k
Le politropiche di riscaldamento per compressione aventi indice compreso tra k e 1 (tra l’adiabatica
e l’isoterma) hanno invece calore specifico negativo e compreso tra 0 e -∞, come è facile
dimostrare considerando che il lavoro fornito dall’esterno durante la compressione è (dalle aree
sottese) evidentemente superiore a quello fornito per realizzare la compressione adiabatica. Per
ottenere la stessa temperatura raggiunta nella compressione adiabatica sarà pertanto necessario
togliere una certa quantità di calore (uscente = negativo). Pertanto cn = (δQ/dT) < 0
dU = - δLk
||
∧ (in valore assoluto)
dU = - δLn<k + δQ
Calore specifico -∞
= compressione isoterma
indice n = 1
Relazioni tra Calori specifici e Indice della politropica
+∞
Cal. Spec. c
cp
cv
-∞
0
0
Isocora
1
Isobara
-∞
Isoterma
k
Indice n
+∞












