Prof. Anna Cristina Mocchetti
gennaio 2008
________________________________________________________________________________________________________________________
LA FUNZIONE INTEGRALE
NEI QUESITI DELL’ESAME DI STATO
Anna Cristina Mocchetti
Le premesse
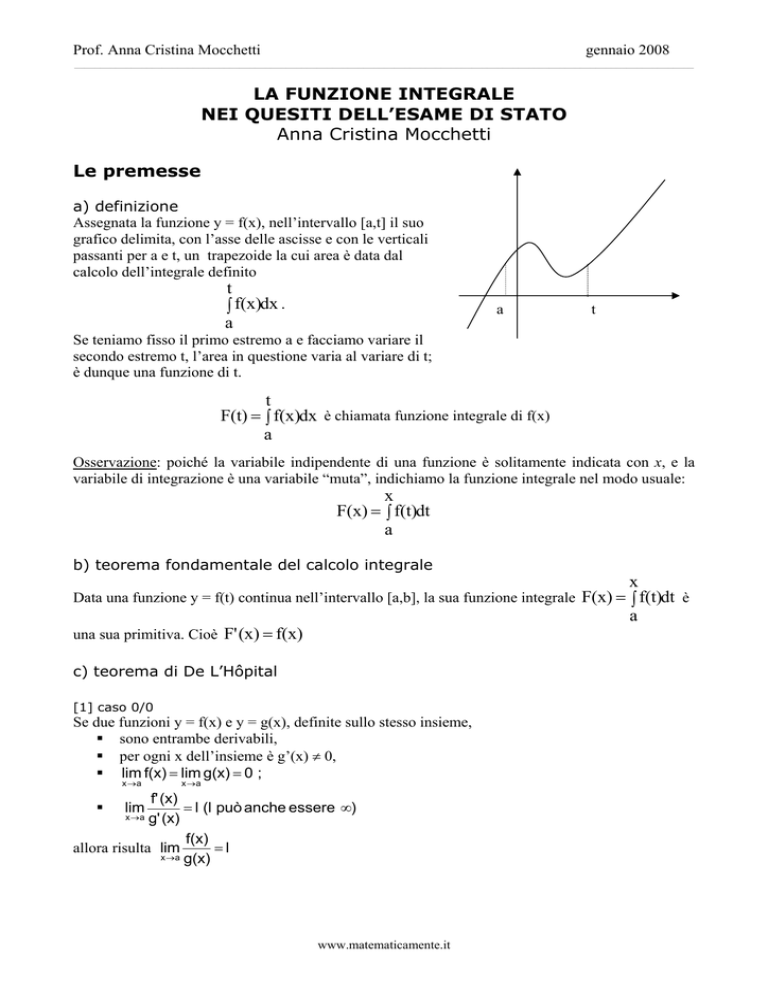
a) definizione
Assegnata la funzione y = f(x), nell’intervallo [a,t] il suo
grafico delimita, con l’asse delle ascisse e con le verticali
passanti per a e t, un trapezoide la cui area è data dal
calcolo dell’integrale definito
t
∫ f(x)dx .
a
a
t
Se teniamo fisso il primo estremo a e facciamo variare il
secondo estremo t, l’area in questione varia al variare di t;
è dunque una funzione di t.
t
F(t) = ∫ f(x)dx è chiamata funzione integrale di f(x)
a
Osservazione: poiché la variabile indipendente di una funzione è solitamente indicata con x, e la
variabile di integrazione è una variabile “muta”, indichiamo la funzione integrale nel modo usuale:
x
F(x) = ∫ f(t)dt
a
b) teorema fondamentale del calcolo integrale
x
Data una funzione y = f(t) continua nell’intervallo [a,b], la sua funzione integrale F(x) = ∫ f(t)dt è
a
una sua primitiva. Cioè F' (x) = f(x)
c) teorema di De L’Hôpital
[1] caso 0/0
Se due funzioni y = f(x) e y = g(x), definite sullo stesso insieme,
sono entrambe derivabili,
per ogni x dell’insieme è g’(x) ≠ 0,
lim f(x) = lim g(x) = 0 ;
x →a
x →a
f' (x)
= l (l può anche essere ∞)
g' (x)
f(x)
allora risulta lim
=l
x →a g(x)
lim
x →a
www.matematicamente.it
Prof. Anna Cristina Mocchetti
gennaio 2008
________________________________________________________________________________________________________________________
[2] caso ∞/∞
Se due funzioni y = f(x) e y = g(x), definite sullo stesso insieme,
sono entrambe derivabili,
per ogni x dell’insieme è g’(x) ≠ 0,
lim f(x) = lim g(x) = ∞ ;
x →a
x →a
f' (x)
lim
= l (l può anche essere ∞)
x →a g' (x)
f(x)
allora risulta lim
=l
x →a g(x)
======================================================================
Liceo Scientifico di ordinamento 2001- sessione ordinaria - Q2
¾ Sia f(x) una funzione reale di variabile reale, continua nel campo reale, tale che f(0)=2.
x
Calcolare lim
x →0
∫ f(t)dt
0
2xe x
dove e è la base dei logaritmi naturali.
Soluzione: nel calcolo del limite richiesto ci troviamo nel caso 0/0 dunque poiché le funzioni al
numeratore e al denominatore soddisfano le ipotesi del t. di De L’Hôpital avremo:
x
∫ f(t)dt
d
(numerator e)
f(x)
2
= lim dx
= lim
= =1
lim 0
x
x
2
x →0 2xe x
x →0 d
(denominat ore) x →0 2 e + xe
dx
(
)
======================================================================
America Latina 2001- sessione ordinaria - Q7
x
¾ Calcolare la derivata rispetto ad x della funzione f(x) tale che f(x) = ∫ te t dt , con x>0, dove
0
e è il numero di Nepero.
Soluzione: per il teorema fondamentale del calcolo integrale f ' (x) = x ⋅ e x
Osservazione: avremmo potuto risolvere l’integrale assegnato e determinare f(x) e poi farne la
derivata come richiesto. Di seguito i passaggi:
x
[
f(x) = ∫ t ⋅ e t dt = t ⋅ e t − ∫ e t dt
0
] = [t ⋅ e
x
0
t
− et
]
x
0
= x ⋅ ex − ex + 1
f ' (x) = e x + x ⋅ e x − e x = x ⋅ e x
======================================================================
www.matematicamente.it
Prof. Anna Cristina Mocchetti
gennaio 2008
________________________________________________________________________________________________________________________
Ordinamento 2001- sessione suppletiva - Q4
¾ Sia f(x) una funzione reale di variabile reale, derivabile con derivata continua in tutto il
x
∫ f(t)dt - x
.
campo reale, tale che f(0)=1 ed f’(0) = 2. Calcolare lim 0
x →0 cos2x - 1
Soluzione: nel calcolo del limite richiesto ci troviamo nel caso 0/0 dunque poiché le funzioni al
numeratore e al denominatore soddisfano le ipotesi del t. di De L’Hôpital avremo:
x
d
(numerator e)
f(x) - 1
dx
0
; ma ancora ci troviamo nella forma di
= lim
= lim
lim
x
x →0 d
x → 0 - 2sen2x
x →0
2xe
(denominat ore)
dx
indecisione 0/0. Applichiamo nuovamente il t. di De L’Hôpital essendo soddisfatte le sue ipotesi e
f' (x)
2
1
=
=−
otteniamo: lim
x →0 - 4cos2x
−4
2
∫ f(t)dt − x
======================================================================
Ordinamento 2002 - sessione ordinaria - Q7
¾ Calcolare la derivata rispetto ad x, della funzione f(x) tale che:
x +1
f(x) =
∫ ln (t)dt
con x > 0.
x
Soluzione: la funzione y = ln(t) è definita e continua in ogni intervallo [x, x+1] con x>0,
x +1
dunque per il teorema fondamentale del calcolo integrale f ' (x) = ln(x + 1) - ln(x) = ln
x
Osservazione: avremmo potuto risolvere l’integrale assegnato e determinare f(x) e poi farne la
derivata come richiesto. Di seguito i passaggi:
x +1
f(x) =
∫ ln(t)dt = [t ⋅ ln(t) − t ]
x
f ' (x) = ln(x + 1) + (x + 1) ⋅
x +1
x
= (x + 1) ⋅ ln(x + 1) − x − 1 − x ⋅ ln(x) + x
1
x +1
− ln(x) − 1 = ln(x + 1) − ln(x) = ln
x +1
x
======================================================================
Autonomia 2002 - sessione ordinaria - Q6
x +2
¾ Calcolare la derivata rispetto ad x della seguente funzione: f(x) =
∫e
-t
dt dove e è la base
x
dei logaritmi naturali.
Soluzione: la funzione y = e-t è definita e continua in ogni intervallo [x, x+2],
⎛ 1
⎞
dunque per il teorema fondamentale del calcolo integrale f ' (x) = e -( x + 2 ) − e − x = e − x ⋅ ⎜ 2 − 1⎟
⎝e
⎠
www.matematicamente.it
Prof. Anna Cristina Mocchetti
gennaio 2008
________________________________________________________________________________________________________________________
Osservazione: anche in questo caso, avremmo potuto risolvere l’integrale assegnato e determinare
f(x) e poi farne la derivata come richiesto. Di seguito i passaggi:
[
f (x) = − e − x
]
x+2
x
= −e - ( x + 2 ) + e − x
⎛ 1
⎞
f ' (x) = e -( x + 2 ) − e − x = e − x ⋅ ⎜ 2 − 1⎟
⎝e
⎠
======================================================================
P.N.I. e Brocca 2002 - sessione ordinaria - Q4
x
¾ Calcolare lim
x →0
∫ sen(t
0
x4
3
)dt
.
Soluzione: nel calcolo del limite richiesto ci troviamo nel caso 0/0; essendo soddisfatte le ipotesi del
t. di De L’Hôpital avremo:
x
d
(numerator e)
sen(x 3 )
dx
0
; ci troviamo nuovamente nella forma di
=
=
lim
lim
lim
x →0
x →0 d
x →0
4x 3
x4
(denominat ore)
dx
indecisione 0/0. Applichiamo nuovamente il t. di De L’Hôpital essendo soddisfatte le sue ipotesi e
3x 2 ⋅ cos(x 3 ) 1
otteniamo: lim
=
x →0
4
12x 2
∫ sen(t
3
)dt
======================================================================
Sperimentale 2002 - sessione suppletiva - Q5
x
1
t2
¾ Calcolare lim 3 ⋅ ∫ 4
dt .
x →0 x
0 t +1
x
Soluzione: il limite assegnato si può scrivere lim
t2
∫0 t 4 + 1 dt
che si presenta nella forma
x3
indeterminata 0/0; il t. di De L’Hôpital ci permette di superare tale forma di indecisione, ottenendo:
x
t2
x2
d
dt
(numerator e)
∫ t4 +1
4
1
dx
lim
lim 0
=
= lim 1 + x2 =
3
x →0
x →0 d
x →0 3x
3
x
(denominat ore)
dx
x →0
======================================================================
America Latina 2002 - sessione suppletiva - Q5
x
¾ Calcolare la derivata, rispetto ad x, della funzione f(x) =
∫
1 − t 2 dt .
0
Soluzione: la funzione assegnata è una funzione composta, essendo l’estremo superiore
d
d
1
(f(x)) = 1 − ( x ) 2 ⋅
dell’integrale una funzione di x;
x = 1− x ⋅
dx
dx
2 x
( )
www.matematicamente.it
Prof. Anna Cristina Mocchetti
gennaio 2008
________________________________________________________________________________________________________________________
Osservazione: Lo stesso risultato si ottiene con calcoli più laboriosi determinando l’integrale
assegnato e poi calcolandone la derivata. Di seguito i passaggi:
∫
1 − t 2 dt
per sostituzione t = senA
= ∫ cos 2 A ⋅ dA = ∫
dt = cosA ⋅ dA
1 + cos(2A)
1
1
1
1
dA = A + sen(2A) = arcsen(t) + t 1 − t 2
2
2
4
2
2
Dunque:
x
f(x) =
∫
1 − t 2 dt =
0
d
1
1
1
arcsen x +
(f(x)) = 1 − x ⋅
x ⋅ 1 − x ; derivando si ottiene
dx
2
2
2 x
======================================================================
Ordinamento 2003 - sessione ordinaria - Q6:
x2
¾ La derivata della funzione f(x) = ∫ e - t dt è la funzione f' (x) = 2x ⋅ e − x Eseguire tutti i
2
4
0
passaggi necessari a giustificare la risposta.
Soluzione: la funzione assegnata è una funzione composta, essendo l’estremo superiore
dell’integrale una funzione di x; ponendo x 2 = g(x) si ha f(x) = Ψ(g(x))
La derivata di una funzione composta si ottiene: f' (x) = Ψ' (g(x)) ⋅ g' (x) e dunque
4
4
d
d 2
(f(x)) = e − x ⋅
x = e − x ⋅ 2x
dx
dx
======================================================================
P.N.I. e Sperimentali 2003 - sessione straordinaria - Q8:
x
¾ Considerata la funzione f(x) = ∫ (1- ln t )dt , con x>0, determinare i suoi zeri e gli intervalli in
0
cui cresce o decresce.
Osservazione: La funzione integranda non è definita in x=0; per determinare f(x) dobbiamo
calcolare un integrale improprio:
x
f(x) = lim
k →0
[t - t ⋅ ln t + t ]k = lim (2x - x ⋅ ln x - 2k + k ⋅ ln k ) = 2x - x ⋅ ln x
∫ (1- ln t )dt = klim
→0
k →0
x
k
La funzione f(x) determinata è definita per x > 0; gli zeri si determinano risolvendo l’equazione
f(x)=0, ossia x⋅(2 - lnx) = 0 da cui lnx = 2 che implica x = e2.
Per determinare gli intervalli in cui cresce o decresce, studiamo il segno della sua derivata prima:
f’(x) = 1- lnx ≥ 0 da cui lnx ≤ 1 vera per 0 < x ≤ e
f(x) cresce nell’intervallo 0 < x < e; decresce per x > e; per x = e, f’(x) = 0 la curva è stazionaria. Il
punto M(e, e) della curva ha la retta tangente orizzontale, esso è un massimo.
======================================================================
www.matematicamente.it
Prof. Anna Cristina Mocchetti
gennaio 2008
________________________________________________________________________________________________________________________
P.N.I. e Sperimentali 2003 - sessione straordinaria - Q10:
∫ (1 - e
x
¾ Calcolare il seguente limite: lim 0
x →0
-t
)dt
essendo e la base dei logaritmi naturali
sen 2 x
Soluzione: il limite assegnato si presenta nella forma indeterminata 0/0; il t. di De L’Hôpital ci
permette di superare tale forma:
∫ (1 - e
x
lim 0
x →0
-t
)dt
sen 2 x
d
(numerator e)
1 − e −x
dx
= lim
= lim
2senxcosx
x →0 d
(denominat ore) x→0
dx
L’ultimo risultato si presenta ancora nella forma di indecisione 0/0; un’ulteriore applicazione del t.
di De L’Hôpital ci permette di ottenere il limite richiesto:
1 − e −x
e −x
1
= lim
=
2
x → 0 2senxcosx
x → 0 2 ⋅ cos 2 x − sen 2 x
lim
(
www.matematicamente.it
)










