soluzioni - maurolabarbera

SOLUZIONI
1)
2)
x3  8
Il lim x 2 4
è:
x  16
0
3
4
1
2
3
8
1
è:
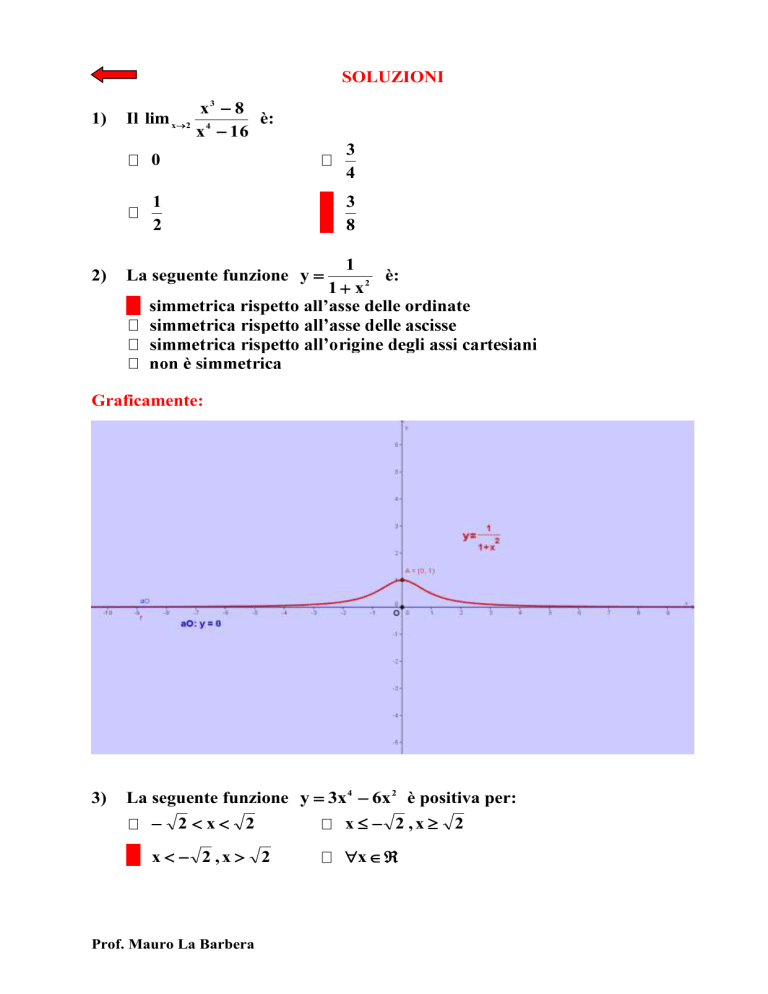
1  x2
simmetrica rispetto all’asse delle ordinate
La seguente funzione y 
Graficamente:
3)
La seguente funzione y  3x 4  6x 2 è positiva per:
 2x 2
x   2 ,x  2
x   2 ,x  2
x  
Prof. Mauro La Barbera
4)
x  
1
è decrescente per:
x2
x   
x    0
x   
La seguente funzione y  
Graficamente:
5)
Calcolare, nel punto di ascissa x 0  3 , la derivata prima della funzione
y  x 2  2x , servendosi della sola definizione di derivata.
Si ha:
f (x)  x 2  2x
f ( x o )  f ( 3)  9  6  3
f (xo  h)  f (3  h)  (3  h)2  2(3  h)  9  h 2  6h  6  2h  h 2  4h  3
Quindi, per la definizione di derivata in un punto, si ottiene:
h 2  4h  3  3
h 2  4h
h(h  4)
f ( 3)  lim h0
 lim h0
 lim ho
 lim ho (h  4)  4
h
h
h
Prof. Mauro La Barbera
6)
Calcolare i punti di minimo e di massimo relativi della funzione:
y  3x 4  6x 2 .
La funzione data ha nei punti A(-1;-3) e B(1;-3) due minimi relativi (e
anche assoluti), mentre ha un massimo relativo nell’origine degli assi
cartesiani.
7)
Calcolare i punti di flesso della funzione:
y  3x 4  6x 2 .
La funzione data ha nel punto C(-√3/3;-5/3) un flesso ascendente a tangente
obliqua e nel punto D(√3/3;-5/3) un flesso discendente a tangente obliqua.
Graficamente:
Torna su
Prof. Mauro La Barbera