
FISICA QUANTISTICA
Dalla delocalizzazione al
teletrasporto passando
per la non località
Lavoro di maturità
Nicola Ghiringhelli
Liceo di Locarno
2004 – 2005
Professore responsabile: Christian Ferrari
Ringraziamenti
I miei ringraziamenti vanno al prof. Christian Ferrari che si è dimostrato un professore modello. Lo ringrazio per la sua disponibilità e gli utili
suggerimenti, anche fuori dalle ore di lezione, e per il suo impegno nel
rispondere puntualmente ai miei quesiti. Sono spesso nate delle interessanti discussioni che mi hanno consentito di approfondire e capire molto
bene l’argomento. Questo lavoro mi ha permesso di vivere una magnifica
esperienza che mi ha dato la possibilità di fare qualcosa che desideravo da
tempo, e per fortuna ho trovato un professore ideale per svolgere in modo
ottimale la mia ricerca.
I
Indice
1 Introduzione
1
2 Primi fenomeni della meccanica quantistica
2.1 Esempio: l’esperimento di Stern-Gerlach . . . . . . . . . . . . . . . . . . .
2.2 Esempio: l’interferometro di Mach-Zehnder . . . . . . . . . . . . . . . . . .
2.3 Esempio: l’interferometro di Franson . . . . . . . . . . . . . . . . . . . . .
3
3
5
6
3 La struttura della meccanica quantistica
3.1 Sistemi semplici e sistemi composti . . . . . . . . . .
3.2 Osservabili . . . . . . . . . . . . . . . . . . . . . . . .
3.3 Fluttuazioni, valore medio e scarto quadratico medio
3.4 Stato . . . . . . . . . . . . . . . . . . . . . . . . . . .
3.4.1 Stato misto . . . . . . . . . . . . . . . . . . .
3.4.2 Stato di conoscenza assoluta . . . . . . . . . .
3.4.3 Stato puro . . . . . . . . . . . . . . . . . . . .
3.4.4 Stato di superposizione . . . . . . . . . . . . .
3.4.5 Stato intrecciato . . . . . . . . . . . . . . . .
3.5 L’equazione agli autovalori . . . . . . . . . . . . . . .
3.6 Probabilità oggettiva . . . . . . . . . . . . . . . . . .
3.7 Misura e postulato della misura ideale . . . . . . . .
3.8 Evoluzione temporale degli stati . . . . . . . . . . . .
3.9 Incompatibilità . . . . . . . . . . . . . . . . . . . . .
3.10 Il Principio di indiscernibilità . . . . . . . . . . . . .
3.11 Complementarità . . . . . . . . . . . . . . . . . . . .
3.12 Delocalizzazione e non località . . . . . . . . . . . . .
4 Esperienze e fenomeni quantistici
4.1 L’esperienza di Stern-Gerlach: il sistema spin 12
4.1.1 Descrizione . . . . . . . . . . . . . . . .
4.1.2 Modellizzazione . . . . . . . . . . . . . .
4.1.3 Riepilogo . . . . . . . . . . . . . . . . .
4.1.4 Discussione . . . . . . . . . . . . . . . .
III
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
9
9
10
10
11
11
12
12
13
14
14
16
17
18
18
19
19
19
.
.
.
.
.
21
21
21
23
27
28
INDICE
IV
4.1.5
4.1.6
4.1.7
Conclusioni . . . . . . . . . . . . . . . . . . . . . . . . . .
Complemento: una nuova proprietà dell’elettrone, lo spin .
Complemento: l’evoluzione temporale dello spin in un
magnetico omogeneo . . . . . . . . . . . . . . . . . . . . .
4.2 L’interferometro di Mach-Zehnder . . . . . . . . . . . . . . . . . .
4.2.1 Descrizione . . . . . . . . . . . . . . . . . . . . . . . . . .
4.2.2 Modellizzazione . . . . . . . . . . . . . . . . . . . . . . . .
4.2.3 Riepilogo . . . . . . . . . . . . . . . . . . . . . . . . . . .
4.2.4 Discussione . . . . . . . . . . . . . . . . . . . . . . . . . .
4.2.5 Conclusioni . . . . . . . . . . . . . . . . . . . . . . . . . .
4.3 L’esperienza di Rauch . . . . . . . . . . . . . . . . . . . . . . . .
4.3.1 Descrizione . . . . . . . . . . . . . . . . . . . . . . . . . .
4.3.2 Modellizzazione . . . . . . . . . . . . . . . . . . . . . . . .
4.3.3 Riepilogo . . . . . . . . . . . . . . . . . . . . . . . . . . .
4.3.4 Discussione . . . . . . . . . . . . . . . . . . . . . . . . . .
4.3.5 Conclusioni . . . . . . . . . . . . . . . . . . . . . . . . . .
4.4 L’interferometro di Franson modificato . . . . . . . . . . . . . . .
4.4.1 Descrizione . . . . . . . . . . . . . . . . . . . . . . . . . .
4.4.2 Modellizzazione . . . . . . . . . . . . . . . . . . . . . . . .
4.4.3 Riepilogo . . . . . . . . . . . . . . . . . . . . . . . . . . .
4.4.4 Discussione . . . . . . . . . . . . . . . . . . . . . . . . . .
4.4.5 Conclusioni . . . . . . . . . . . . . . . . . . . . . . . . . .
4.5 Il Teletrasporto . . . . . . . . . . . . . . . . . . . . . . . . . . . .
4.5.1 Introduzione . . . . . . . . . . . . . . . . . . . . . . . . . .
4.5.2 Descrizione . . . . . . . . . . . . . . . . . . . . . . . . . .
4.5.3 Modellizzazione . . . . . . . . . . . . . . . . . . . . . . . .
4.5.4 Riepilogo . . . . . . . . . . . . . . . . . . . . . . . . . . .
4.5.5 Discussione . . . . . . . . . . . . . . . . . . . . . . . . . .
4.5.6 Conclusioni . . . . . . . . . . . . . . . . . . . . . . . . . .
5 Conclusione
. . . .
. . . .
campo
. . . .
. . . .
. . . .
. . . .
. . . .
. . . .
. . . .
. . . .
. . . .
. . . .
. . . .
. . . .
. . . .
. . . .
. . . .
. . . .
. . . .
. . . .
. . . .
. . . .
. . . .
. . . .
. . . .
. . . .
. . . .
. . . .
. 30
. 30
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
31
35
35
36
40
42
43
45
45
47
49
50
51
52
52
53
55
55
63
64
64
64
67
70
71
72
75
A Esempio classico: il valore medio, lo stato misto e lo stato di conoscenza
assoluta
79
B Alcune proprietà dello spazio di Hilbert H = C2 e delle matrici
81
Bibliografia
83
Elenco delle figure
2.1
2.2
2.3
2.4
Primo esperimento di Stern-Gerlach semplificato. .
Secondo esperimento di Stern-Gerlach semplificato.
L’esperimento di Mach-Zehnder semplificato. . . . .
L’esperimento di Franson semplificato. . . . . . . .
4.1
4.2
Schematizzazione dell’apparecchio di Stern-Gerlach. . . . . . . . . . . . . .
Montaggio dell’esperienza di Stern-Gerlach: si notano il campo magnetico
disomogeneo e i due soli risultati della misura (spin up = +1; spin down =
−1). . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Documento originale della distribuzione degli atomi: a destra con il campo
magnetico disomogeneo, a sinistra senza campo magnetico. . . . . . . . . .
Previsione dei risultati dell’esperienza. . . . . . . . . . . . . . . . . . . . .
Primo esperimento di Stern-Gerlach. . . . . . . . . . . . . . . . . . . . . .
Secondo esperimento di Stern-Gerlach. . . . . . . . . . . . . . . . . . . . .
Primo esperimento di Mach-Zehnder. . . . . . . . . . . . . . . . . . . . . .
Secondo esperimento di Mach-Zehnder: da notare che con l’allungamento
di percorso φ i risultati dell’esperienza si invertono. . . . . . . . . . . . . .
Schema dell’esperienza di Rauch. . . . . . . . . . . . . . . . . . . . . . . .
Schema dei tre separatori di fascio verticali e del campo magnetico omogeneo.
A sinistra: foto del montaggio originale dell’esperienza di Rauch. A destra:
foto dei tre separatori di fascio verticali, schematizzati nella figura 4.10. . .
Esperienza con l’interferometro di Franson. . . . . . . . . . . . . . . . . . .
Schema del protocollo di teletrasporto. . . . . . . . . . . . . . . . . . . . .
4.3
4.4
4.5
4.6
4.7
4.8
4.9
4.10
4.11
4.12
4.13
V
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
3
4
5
6
22
22
23
23
28
29
35
36
45
46
46
52
66
Capitolo 1
Introduzione
Prologo
Un secolo fa il fisico tedesco Max Planck svelava i primi segreti della fisica quantistica1 .
Cosı̀ come la relatività generale e quella ristretta di Einstein danno uno scossone alla
nostra visione del mondo per quello che riguarda le situazioni in cui un corpo è molto
veloce o molto massiccio, la meccanica quantistica fa lo stesso - se non di più - per oggetti
molto piccoli, a livello atomico e subatomico. La meccanica quantistica ci mostra senza
ombra di dubbio che alcuni concetti basilari nel mondo macroscopico perdono di significato
in quello microscopico. Quindi dobbiamo modificare linguaggi e modi di ragionare se
vogliamo capire come funzionano le cose a scale piccolissime.
Prefazione
Questo testo vuole coinvolgere il lettore, facendogli capire come la fisica quantistica vada
contro il nostro intuito portando a delle conseguenze straordinarie, come per esempio il
teletrasporto.
Ho cercato di dare la massima flessibilità alla lettura del testo: i capitoli e i sottocapitoli sono legati fra loro attraverso molti riferimenti, messi in evidenza dalla dicitura
“(v.cap. )”. L’obiettivo è arrivare a capire il teletrasporto e soprattutto le molteplici
innovazioni concettuali introdotte dalla fisica quantistica.
Struttura del testo
Dapprima, nel capitolo 2, sono presentate in modo molto semplificato tre esperienze
significative, che saranno approfondite nel capitolo 4, con lo scopo di stuzzicare la
curiosità del lettore, dandogli un’idea degli “strani” effetti della fisica quantistica. Nel
capitolo 3 sono spiegati gli strumenti della teoria quantistica necessari per affrontare le
1
Useremo i termini meccanica quantistica, fisica quantistica e teoria quantistica in modo equivalente.
1
1. Introduzione
2
modellizzazioni delle esperienze. Il capitolo 4 è dedicato alle esperienze e ai fenomeni
quantistici più importanti. Ogni esperienza è suddivisa in quattro sezioni principali:
• la descrizione, in cui è descritto il montaggio dell’esperimento considerato e cosa si
osserva.
• la modellizzazione, in cui si formalizza la descrizione applicando le conoscenze
teoriche apprese nel capitolo 3.
• il riepilogo, in cui sono riassunti gli elementi principali che saranno poi utilizzati
nella discussione.
• la discussione, in cui si analizzano gli effetti che l’esperienza mette in evidenza.
• le conclusioni, in cui sono elencati i concetti fondamentali che si sono ricavati
dall’esperienza.
Nel capitolo 5 si discutono le conseguenze e le interpretazioni della fisica quantistica in
confronto ad una visione classica della fisica. Infine nell’appendice A è spiegato un esempio
tratto dalla fisica classica in relazione al capitolo 3, e nell’appendice B sono elencate
alcune regole di matematica utili per eseguire le dimostrazioni e i calcoli delle parti più
approfondite dei capitoli 3 e 4, che richiedono determinate conoscenze matematiche.
Capitolo 2
Primi fenomeni della meccanica
quantistica
Prima di analizzare la struttura di un sistema quantistico, è preferibile iniziare a presentare al lettore degli esempi semplificati di esperienze quantistiche, che dovrebbero
aiutare a capire come la fisica quantistica abbia rivoluzionato il mondo delle scienze esatte. È importante fermarsi un attimo a riflettere sull’illogicità apparente delle conclusioni
a cui porteranno gli esperimenti esposti in seguito, perché sono alla base del “mondo
quantistico”.
2.1
Esempio: l’esperimento di Stern-Gerlach
Prima esperienza (v. Figura 2.1)
Figura 2.1: Primo esperimento di Stern-Gerlach semplificato.
Descrizione dell’immagine:
• in giallo e celeste delle biglie;
• in verde due apparecchi di misura di un certo tipo A, che separano le biglie gialle
da quelle celesti;
• in rosso la traiettoria delle biglie.
3
2. Primi fenomeni della meccanica quantistica
4
Cosa succede: le biglie gialle sono deviate dal primo apparecchio A verso la sua sinistra,
mentre quelle celesti verso la sua destra. Nel secondo apparecchio, sempre di tipo A,
giungono le biglie gialle appena deviate dal primo, che saranno tutte deviate nuovamente
verso sinistra e non ci sarà nessuna biglia che verrà indirizzata a destra, poiché tutte le
biglie celesti sono state scartate dal primo dispositivo A. Tutto va finora come il nostro
intuito predirebbe.
Seconda esperienza (v. Figura 2.2)
Figura 2.2: Secondo esperimento di Stern-Gerlach semplificato.
Descrizione dell’immagine:
• in giallo e celeste delle biglie;
• in verde due apparecchi di misura uguali di un certo tipo A, che separano le biglie
gialle da quelle celesti;
• in arancione un apparecchio di misura diverso di un certo tipo B, che spartisce
equamente le biglie gialle a destra e a sinistra;
• in rosso la traiettoria delle biglie, che sono deviate.
Cosa succede: le biglie gialle sono deviate dal primo apparecchio A verso la sua sinistra,
mentre quelle celesti verso la sua destra. Nel secondo apparecchio, questa volta diverso
dal primo quindi di tipo B, giungono le biglie gialle appena deviate dal primo, che saranno
deviate nuovamente in media una volta verso sinistra e una volta verso destra. Nel terzo
dispositivo, di tipo A quindi uguale al primo, ci si aspetterebbe che non vi sia alcuna
biglia indirizzata verso destra, poiché tutte le biglie celesti sono state scartate dal primo
dispositivo A. Invece non è cosı̀: i risultati mostrano che anche verso destra sono state
deviate delle biglie.
Si può affermare che ogni biglia esce dal secondo apparecchio di misura metà gialla e metà
celeste ?
2. Primi fenomeni della meccanica quantistica
2.2
5
Esempio: l’interferometro di Mach-Zehnder
Figura 2.3: L’esperimento di Mach-Zehnder semplificato.
Descrizione dell’immagine:
• in arancione una biglia;
• in celeste due separatori uguali, che al 50% fanno passare la biglia diritta e al 50%
la deviano verso il basso (in modo casuale);
• in rosso due pareti che indirizzano la biglia verso il secondo separatore celeste;
• in blu le traiettorie possibili della biglia;
• in verde e giallo due contenitori uguali che raccolgono le biglie.
Cosa succede: si lanciano molte biglie nel montaggio raffigurato, prestando attenzione che
la biglia successiva non venga tirata prima che quella precedente sia arrivata in uno dei
due contenitori. Si noti che la lunghezza del cammino è uguale, sia che la biglia passi dalla
parete in basso sia da quella in alto. Ragioniamo ora secondo il nostro intuito. Una biglia
dopo il primo separatore si trova a percorrere il cammino verticale con una probabilità del
50% e quando giunge al secondo separatore ha il 50% di possibilità di finire nel contenitore
giallo e il 50% in quello verde, nel complesso al 25% cadrà nel recipiente giallo e al 25%
in quello verde. Lo stesso ragionamento vale anche se la biglia avesse preso il cammino
orizzontale dopo il primo separatore, cioé ha il 25% delle possibilità di terminare nel
contenitore giallo e il 25% in quello verde. Quindi lanciando tante biglie, sempre una alla
volta, le nostre aspettative di trovarle nel recipiente giallo saranno del 25%+25%=50% e
in quello verde del 25%+25%=50%. Invece eseguendo la verifica sperimentale delle nostre
attese, si scopre un risultato strano: nessuna biglia è finita nel recipiente giallo, ma tutte
2. Primi fenomeni della meccanica quantistica
6
sono finite in quello verde.
Come può essere spiegato questo strano risultato ?
2.3
Esempio: l’interferometro di Franson
Figura 2.4: L’esperimento di Franson semplificato.
Descrizione dell’immagine:
• in arancione una coppia di biglie;
• in celeste quattro separatori uguali, che al 50% fanno proseguire la biglia diritta e
al 50% la deviano verso l’alto (risp. il basso), in modo casuale;
• in rosso delle pareti che indirizzano la biglia sulla traiettoria indicata;
• in blu le traiettorie possibili delle due biglie;
• in verde e giallo quattro contenitori uguali che raccolgono le biglie. Da notare che
questa esperienza è composta da due montaggi simmetrici simili a quello precedente,
di Mach-Zehnder.
Cosa succede: si lanciano molte coppie di biglie nel montaggio raffigurato (una biglia della
coppia verso sinistra e l’altra verso destra), prestando attenzione che la coppia di biglie
successiva non venga tirata prima che le biglie della coppia precedente siano finite nei
contenitori. Alla fine dell’esperimento, guardano solo la parte sinistra (o la parte destra)
del montaggio, si nota che il 50% delle biglie sono giunte nel contenitore verde e il 50%
in quello giallo. Se si confrontano i risultati di ogni coppia di biglie, si constata però che
se una biglia della coppia è arrivata nel recipiente verde allora anche l’altra è arrivata
sempre in quello verde, e analogamente se è giunta nel contenitore giallo si osserva che
pure l’altra è arrivata sempre in quello giallo. Quindi sembrerebbe che le biglie di ogni
coppia si comportassero allo stesso modo, poichè entrambe giungono sempre nello stesso
contenitore. Sarà vero ?
2. Primi fenomeni della meccanica quantistica
7
Cos’è successo in queste tre esperienze? Lo scoprirete nel seguito del testo. . . le sorprese
non sono finite. . . buona lettura. . .
Capitolo 3
La struttura della meccanica
quantistica
È giunto il momento di presentare il formalismo necessario per poter capire le diverse
situazioni della meccanica quantistica proposte in seguito. Magari a prima vista può
sembrare complesso e troppo matematico, ma vedrete che dopo aver familiarizzato con
i suoi concetti sarete in grado di sfruttare appieno le sue potenzialità. È importante
riuscire a staccarsi da interpretazioni classiche dei risultati della fisica quantistica per
evitare di perdersi poi in paradossi e situazioni ancor più di difficili da capire. Inoltre
non dimenticatevi che tutti gli effetti strani che spiegheremo avvengono con particelle
microscopiche, ma non fra oggetti macroscopici che noi riusciamo a vedere.
Nei tre esempi iniziali ho cercato di semplificare al massimo le situazioni: in realtà non
sono state usate né biglie né semplici apparecchi, ma sistemi ben più complessi. Spesso
per capire il “cuore” del problema è utile schizzare dapprima l’esperienza e solo in un
secondo tempo andare a studiarne tutte le caratteristiche.
I concetti fondamentali della fisica quantistica sono quelli di sistema, di osservabile
e di stato. Pure in fisica classica ritroviamo questi tre elementi, anche se ci sono delle
differenze fondamentali, che scopriremo via via nel testo.
3.1
Sistemi semplici e sistemi composti
In fisica ciò che si vuole studiare è chiamato sistema. Un sistema può quindi essere un
carrellino che si sposta su una rotaia oppure l’universo intero; a dipendenza di quello che
si vuole studiare scegliamo un sistema appropriato.
I sistemi sono suddivisi in due tipi: semplici o composti. I sistemi semplici sono quelli
in cui si ha una sola particella, per esempio l’interferometro di Mach-Zehnder, dove si
considera la direzione di propagazione di una particella.
I sistemi composti sono quelli in cui si prendono in considerazione due o più particelle che possono essere spazialmente separate, come per esempio nell’esperienza di Franson,
9
3. La struttura della meccanica quantistica
10
dove si studia la direzione di propagazione di due particelle contemporaneamente.
Riferendomi al seguito del testo, considereremo sistemi semplici quali: un atomo di argento nell’apparecchio di Stern-Gerlach (v.cap. 4.1), una particella nell’interferometro di
Mach-Zehnder (v.cap. 4.2), un neutrone nell’interferometro di Rauch (v.cap. 4.3). Per
quanto riguarda i sistemi composti tratteremo: una coppia di particelle nell’interferometro
di Franson (v.cap. 4.4) e il teletrasporto (v.cap. 4.5).
3.2
Osservabili
Affinché si possa analizzare un sistema, si devono avere delle grandezze fisiche che si
possano misurare, chiamate osservabili . Esse sono quindi legate a degli apparecchi
di misura: è grazie a loro che possiamo sapere, per esempio, il valore dell’osservabile posizione di una particella che si sposta con un moto rettilineo uniforme.
In meccanica quantistica un’osservabile è rappresentata da una matrice
autoaggiunta 1
A ∈ {A ∈ M2 (C) : A = A∗ } = A
Matematicamente l’insieme delle osservabili ha la struttura di un’algebra, notata A.
Ogni osservabile si può scrivere nella forma
A=
2
X
λi Pλi
(3.1)
i=1
con λi ∈ R gli autovalori di A (v.cap. 3.5) e Pλi il proiettore associato all’autovettore di
λi (grazie al teorema spettrale, [2]).
Per una presentazione di alcuni concetti di algebra (lineare), quali il campo dei numeri
complessi, lo spazio di Hilbert Cn , le matrici e il prodotto tensoriale, consultate [2].
3.3
Fluttuazioni, valore medio e scarto quadratico
medio
Il valore di un’osservabile non sempre ha un solo valore ben preciso, sia in fisica classica
che quantistica. Spesso misurando più volte un’osservabile A, sempre con il sistema nelle
medesime “condizioni” (cioè nello stesso stato), si ottengono valori diversi. Si hanno
perciò delle fluttuazioni del valore dell’osservabile.
Per caratterizzare queste fluttuazioni si ricorre allo scarto quadratico medio di A
(indicato con ∆A ) nello stato ρ̂, definito da
q
q
2
2
oppure
(∆A )ρ̂ = h(A − hAiρ̂ )2 iρ̂
(∆A )ρ̂ = hA iρ̂ − hAiρ̂
1
In questo testo ci limitiamo sovente a considerare lo spazio di Hilbert H = C2 . Va però detto che la
meccanica quantistica considera anche spazi di altre dimensioni, per esempio H = C4 .
3. La struttura della meccanica quantistica
11
Il valore medio di un’osservabile A nello stato2 ρ̂, indicato con hAiρ̂ , è la somma
di ogni suo valore possibile moltiplicato per la probabilità con cui esso si presenta
nell’esperienza.
Nell’appendice A, pagina 79 è presentato un esempio di un sistema classico dove
viene calcolato il valore medio di un’osservabile, che aiuta a comprendere il significato di
valore medio e stato.
3.4
Stato
Lo stato del sistema rappresenta l’informazione che l’osservatore ha sul sistema considerato.
Matematicamente lo stato è rappresentato da un’applicazione
ρ : A −→ R
A 7−→ hAiρ̂
che deve essere lineare, positiva (hA2 iρ̂ ≥ 0) e normata (hIiρ̂ = 1).
In meccanica quantistica uno stato (generale) del sistema è rappresentato da
una matrice densità ρ̂ ∈ M2 (C), che deve quindi soddisfare:
• ρ̂ ≥ 0 =⇒ ρ̂ = ρ̂∗
• T r(ρ̂) = 1
In meccanica quantistica si parla di stati misti, puri, di superposizione e
intrecciati .
Vediamo di cosa si tratta.
3.4.1
Stato misto
Gli stati misti sono quelli che danno solo una conoscenza parziale, ossia di tipo
statistico, del sistema, che è dovuta a una mancanza di informazioni dell’osservatore.
Quindi delle misure del valore di un’osservabile A, in uno stato misto, avranno delle
fluttuazioni, ossia ∆A > 0, proprio perché l’osservatore non conosce tutte le informazioni
del sistema che potrebbe sapere.
Gli stati misti sono rappresentati dalle matrici densità indicate con ρ̂, come quella scritta
poco fa.
Se il sistema è nello stato misto ρ̂ allora
hAiρ̂ = T r(ρ̂A)
2
Tra breve approfondiremo il concetto di stato.
(3.2)
3. La struttura della meccanica quantistica
3.4.2
12
Stato di conoscenza assoluta
Quando un’osservabile A non ha fluttuazioni nella misura del suo valore per
uno stato dato, ovvero quando ∆A = 0, lo stato che ne descrive il sistema è detto di
conoscenza assoluta per l’osservabile A. Ciò significa che la probabilità di osservare
un certo valore λ0 in una misura dell’osservabile A è 1 e per tutti gli altri valori λi possibili
la probabilità è 0.
3.4.3
Stato puro
Lo stato puro dà una conoscenza massimale sul sistema. Per alcune osservabili A nello
stato puro si ha ∆A > 0. A differenza di uno stato misto, questa apparente3
mancanza di conoscenza del sistema è indipendente dall’osservatore, poiché
è la situazione fisica stessa che non permette una conoscenza assoluta.
Come vedremo più avanti, gli stati puri prediranno i valori delle osservabili con delle
probabilità oggettive (v.cap. 3.6), quindi in meccanica quantistica il risultato di
una misura dipende oggettivamente dal caso, ma non dall’osservatore.
L’insieme degli stati puri ha la struttura di uno spazio vettoriale di Hilbert H, perciò ogni
vettore ψ rappresenta uno stato del sistema. Infatti uno stato puro è rappresentato da
un proiettore
(ψ, •)ψ
ρ̂ =⇒ Pψ =
||ψ||2
vale a dire una matrice densità ρ̂ che deve soddisfare anche ρ̂ = ρ̂2 . Inoltre
T r(ρ̂) = 1, ciò significa che Pψ è un proiettore unidimensionale.
Visto che l’insieme dei vettori linearmente dipendenti a ψ genera lo stesso sottospazio
vettoriale unidimensionale, ossia lo stesso proiettore, possiamo affermare che uno stato
puro di un sistema è dato da un vettore ψ dello spazio di Hilbert H e tutti
i vettori che gli sono linearmente dipendenti rappresentano lo stesso stato
puro.
Se lo stato puro ψ è un autovettore4 di un’osservabile A, allora lo stato ψ rappresenta uno stato di conoscenza assoluta per l’osservabile A.
Anticipiamo che ovviamente, per un sistema in un stato puro, il risultato di una misura
è conosciuto solo in modo probabilistico, ma affronteremo meglio questo argomento nel
capitolo 3.6.
Se il sistema è nello stato puro rappresentato dal vettore ψ normalizzato, allora il
3
È fondamentale sottolineare che è solo apparente, altrimenti la teoria quantistica non sarebbe una
teoria completa.
4
Vedi la sezione dell’equazione agli autovalori (cap. 3.5).
3. La struttura della meccanica quantistica
13
valore medio dell’osservabile A è dato da
hAiψ = (ψ, Aψ)
dove A è la matrice (autoaggiunta) che rappresenta l’osservabile A (v.cap. 3.2). Per
dimostrare questo risultato, nel caso H = C2 , si sfrutta che hAiρ̂ = T r(ρ̂A) = T r(Pψ A)
poiché ρ̂ ≡ Pψ e sviluppando, supponendo che {e1 = ψ, e2 = ϕ} sia una base ortonormata
di C2 , si ha
T r(Pψ A) = T r(APψ ) =
2
X
=ψ
=0
z}|{
z}|{
(ei , APψ ei ) = (ψ, A Pψ ψ) + (ϕ, A Pψ ϕ) = (ψ, Aψ)
i=1
Nella tabella 3.1 sono messi a confronto lo stato puro, quello misto e quello di conoscenza
assoluta.
Stato puro ψ
Stato misto ρ̂
⇐⇒ Stato di conoscenza massimale ⇐⇒ Stato di conoscenza parziale
(∆A )ψ > 0
(∆A )ρ̂ > 0
Informazione non statistica
Informazione statistica
Stato di conoscenza assoluta
⇐⇒ Per certe osservabili A, se (∆A )ψ = 0
Tabella 3.1: Stati misti, puri e di conoscenza assoluta a confronto.
3.4.4
Stato di superposizione
Gli stati di superposizione rappresentano una delle caratteristiche fondamentali della meccanica quantistica, ossia il principio di sovrapposizione di stati puri5 . Quindi uno stato
di superposizione è della forma
ψ = αψ1 + βψ2
con |α|2 + |β|2 = 1
ossia una combinazione lineare degli stati puri ψ1 e ψ2 .
Esso è ancora un vettore di C2 , ed è quindi uno stato puro.
Questi stati non esistono in una teoria classica, ma si possono interpretare
dicendo che “il sistema si trova potenzialmente nello stato ψ1 e nello stato
ψ2 ”.
I sistemi semplici che tratteremo sono detti sistemi a due livelli , poiché:
• Le osservabili saranno delle matrici autoaggiunte 2 × 2 del tipo A ∈ M2 (C).
• Gli stati puri saranno vettori del tipo ψ ∈ H = C2 .
5
Anche in fisica classica esiste un analogo principio: quello della sovrapposizione delle onde, ma non
è da confondere con quello della fisica quantistica.
3. La struttura della meccanica quantistica
3.4.5
14
Stato intrecciato
Gli stati intrecciati sono quelli che si usano per rappresentare gli stati dei sistemi composti (v.cap. 3.1), dove si considerano due (o più) particelle contemporaneamente. In
questi sistemi si deve introdurre una notazione che unisce lo spazio di Hilbert che descrive gli stati della prima particella con lo spazio di Hilbert che descrive gli stati della
seconda particella, usando il prodotto tensoriale ⊗.
Gli stati puri dei sistemi composti che tratteremo sono quindi dei vettori dello spazio di Hilbert H = H1 ⊗H2 , dove H1 è lo spazio di Hilbert C2 degli stati del primo sistema
e H2 è lo spazio di Hilbert C2 degli stati del secondo sistema. Per esempio lo stato ψ1 ⊗ ψ2
rappresenta uno stato puro di un sistema composto (formato da due particelle), in cui lo
stato puro della prima particella è ψ1 e quello della seconda è ψ2 .
Uno stato intrecciato è una combinazione lineare di vettori dello spazio C2 ⊗ C2 , ossia
della forma
Ψ = α(ψ1 ⊗ ψ2 ) + β(ϕ1 ⊗ ϕ2 ) con |α|2 + |β|2 = 1
dove ψ1 , ϕ1 ∈ H1 e ψ2 , ϕ2 ∈ H2 .
Gli stati intrecciati 6 sono tutti quegli stati di H = C2 ⊗ C2 che non possono essere
scritti nella forma ψ1 ⊗ ψ2 (cioè non fattorizzabili ).
3.5
L’equazione agli autovalori
Ci sono tre importanti risultati riferiti agli autovalori, sono cosı̀ enunciati:
(1) Quando si misura un’osservabile si possono osservare solo gli autovalori (che sono numeri reali) associati alla sua matrice.
(2) Sia ψ uno stato puro.
A se è un suo autovettore.
Esso è uno stato di conoscenza assoluta per
(3) Se ψ è un autovettore dell’osservabile A, allora ψ è uno stato di conoscenza assoluta per l’osservabile A.
Dimostriamo la (2). Se ψ è uno stato di conoscenza assoluta per un’osservabile A,
lo scarto quadratico medio (v.cap. 3.3) è ovviamente nullo, ossia (∆A )ψ = 0. Inoltre
(∆A )ψ = 0 = (∆A )2ψ = 0, calcolando lo scarto quadratico medio si ha
=B
z }| {
(∆A )2ψ = h (A − hAiψ ) 2 iψ = (ψ, B 2 ψ) = (B ∗ ψ, Bψ) = (Bψ, Bψ)
= ||Bψ||2 =⇒ ||Bψ||2 = 0 ⇐⇒ ||Bψ|| = 0
6
Qui ci riferiamo solo agli stati puri intrecciati.
proprietà norma
⇐⇒
Bψ = 0
3. La struttura della meccanica quantistica
15
Reinserendo B(= A − hAiψ ) si ha
(A − hAiψ )ψ = 0 =⇒ Aψ − hAiψ ψ = 0 =⇒ Aψ = hAiψ ψ
Visto che7 (∆A )ψ = 0, il valore λ di A è esatto (e fisso), ossia hAiψ = λ. Quindi
=⇒ Aψ = λψ
Quest’equazione si chiama equazione agli autovalori dell’osservabile A. Il
valore λ è detto autovalore (dell’osservabile A) e il vettore ψ 6= 0 è detto autovettore
(dell’osservabile A).
Dimostriamo la (3). Se ψ è un autovettore di un’osservabile A, si ha Aψ = λψ.
Lo scarto quadratico medio di A nello stato ψ elevato al quadrato è (v. cap. 3.3)
(∆A )2ψ = hA2 iψ − hAi2ψ = (ψ, A2 ψ) − (ψ, Aψ)2
(3.3)
Calcoliamo separatamente questi due ultimi prodotti scalari:
=1
=λψ
z }| {
z}|{
(ψ, A2 ψ) = (A∗ ψ, Aψ) = (Aψ, Aψ ) = (λψ, λψ) = ||λψ||2 = |λ|2 ||ψ||2 = λ2
e
=1
z}|{
(ψ, Aψ) = (ψ, λψ) = λ (ψ, ψ) = λ ||ψ||
2
2
2
2
2
= λ2
Reinserendo nella (3.3) i rispettivi risultati, si ha
(ψ, A2 ψ) − (ψ, Aψ)2 = λ2 − λ2 = 0 = (∆A )2ψ ⇐⇒ (∆A )ψ = 0
Se lo scarto quadratico medio è nullo, significa che non vi sono fluttuazioni e che quindi
l’autovettore ψ è uno stato di conoscenza assoluta per l’osservabile A.
Importante:
L’equazione agli autovalori di un’osservabile, è espressa nella forma
Aϕ = λϕ
dove A è l’osservabile (matrice autoaggiunta), ϕ 6= 0 è il suo autovettore (stato
puro di conoscenza assoluta per A) e λ l’autovalore (valori osservabili) associato
all’autovettore ϕ.
7
Questo significa che lo stato puro ψ è anche uno stato di conoscenza assoluta per l’osservabile A.
3. La struttura della meccanica quantistica
3.6
16
Probabilità oggettiva
Come detto in precedenza le situazioni fisiche stesse non permettono sempre di avere
una conoscenza assoluta sul sistema e di predire con certezza il valore delle osservabili. È
quindi necessario ricorrere a delle probabilità oggettive di osservare un certo autovalore
dell’osservabile considerata: conoscendo lo stato del sistema è possibile calcolare
la probabilità di osservare un valore λi (ossia un autovalore di A), in una
misura di un’osservabile A.
La probabilità di osservare il valore λi di un’osservabile A, se il sistema è nello
stato misto ρ̂, è data da
Probρ̂ {A = λi } = T r(ρ̂Pλi )
dove Pλi è il proiettore sull’autovettore il cui autovalore è λi e ricordiamo che T r(. . .) è
la traccia, ossia “la somma degli elementi diagonali di una matrice”.
Dimostriamo questo risultato. Quando si misura un’osservabile si possono osservare solo
gli autovalori associati alla sua matrice, si ha perciò
hAiρ̂ =
2
X
λi Probρ̂ {A = λi }
(3.4)
i=1
dove Probρ̂ {A = λi } è la probabilità di osservare l’autovalore λi dell’osservabile A se il
sistema è nello stato rappresentato da ρ̂.
Dalla (3.2), sostituendo A con la (3.1), si vede che il valore medio di A si può scrivere
anche cosı̀
!
2
2
X
X
hAiρ̂ = T r ρ̂
λi Pλi =
λi T r(ρ̂Pλi )
(3.5)
i=1
i=1
Quindi, confrontando la (3.4) e la (3.5), si conclude che
Probρ̂ {A = λi } = T r(ρ̂Pλi )
Nel caso in cui il sistema è nello stato puro rappresentato dal vettore ψ normalizzato
(||ψ|| = 1), la probabilità di trovare il valore λi è
Probψ {A = λi } = ||Pλi ψ||2
Infatti, come abbiamo visto precedentemente hAiψ = (ψ, Aψ) e A si può scrivere anche
P
A = 2i=1 λi Pλi , quindi si ha
hAiψ = (ψ,
2
X
i=1
=
2
X
i=1
λi (ψ, Pλ2i ψ)
=
2
X
i=1
λi Pλi ψ) =
2
X
λi (ψ, Pλi ψ)
i=1
λi (Pλ∗i ψ, Pλi ψ)
=
2
X
i=1
λi (Pλi ψ, Pλi ψ)
3. La struttura della meccanica quantistica
=
2
X
λi ||Pλi ψ||2
17
(3.6)
i=1
P
Per analogia, sappiamo che hAiψ = 2i=1 λi Prob{A = λi }, quindi paragonando con la
(3.6) si conclude che
Probψ {A = λi } = ||Pλi ψ||2
È importante notare che questa probabilità dipende solamente dall’osservabile considerato e dallo stato puro ψ e non dall’osservatore, è per questo
motivo che si parla di probabilità oggettive.
Se il sistema è nello stato di conoscenza assoluta per l’osservabile A, rappresentato dall’autovettore normalizzato ψ di A, abbiamo un caso particolare dello stato
puro in cui la probabilità di osservare l’autovalore λψ associato all’autovettore ψ è
Probψ {A = λψ } = 1
e ovviamente è 0 per tutti gli altri valori λi 6= λψ .
Le probabilità oggettive, tipiche quando il sistema è in uno stato di superposizione, permettono di affermare che questi stati sono associati a delle proprietà potenziali
che poi grazie al processo di misura si dice che si attualizzano (v. cap 3.7,
postulato della misura ideale). A questo istante si osserverà solamente un certo valore
λ. Per esempio nel caso di uno stato di superposizione (v.cap. 3.4.4), il sistema è solo
potenzialmente nello stato ψ1 e ψ2 : procedendo alla misura si attualizzerà solo uno dei
due stati. Se cosı̀ non fosse, ovvero se le potenzialità non si attualizzassero, una particella
in uno stato di superposizione si dovrebbe “dividere in due”.
3.7
Misura e postulato della misura ideale
Il processo di misura, cioè l’interazione degli strumenti di misura dell’osservatore con
il sistema, è uno dei punti che sono tuttora piuttosto oscuri in meccanica quantistica.
Si constata che il processo di misura porta a una modifica non deterministica dello
stato, ciò significa che conoscendo lo stato al tempo t0 non è possibile determinare con
certezza quale esso sarà a un istante t qualsiasi dopo la misura. Ci sono due postulati
fondamentali legati alla misura, che sono riassunti nel
Postulato della misura ideale
1. Postulato della riduzione dello stato: Immediatamente dopo la misura dell’osservabile A, in cui è stato osservato il valore λ, lo stato del sistema (qui supposto puro) è uno stato di conoscenza assoluta per A, ossia uno stato tale che
3. La struttura della meccanica quantistica
18
Probψ {A = λ} = ||Pλ ψ||2 = 1, quindi lo stato (subito dopo aver osservato il valore
λ) è rappresentato dall’autovettore ϕ associato a λ. In altre parole se lo stato prima della misura era uno stato di superposizione ψ = αψ1 + βψ2 , con ψ1 il vettore
associato al risultato +1 e ψ2 quello associato a −1, dopo la misura se si osserva il
valore +1 allora lo stato del sistema è ψ1 , invece se si osserva −1 è ψ2 .
2. Per ogni osservabile B compatibile (v.cap. 3.9) con A, il cui il valore era esattamente conosciuto prima della misura di A, si ha che immediatamente dopo la misura
dell’osservabile A il valore di B non è stato modificato dalla misura di A.
3.8
Evoluzione temporale degli stati
L’evoluzione di uno stato, di qualsiasi tipo, in un sistema quantistico è
un processo deterministico8 : ciò significa che conoscendo lo stato ad un istante t0
è possibile sapere quale sarà lo stato all’istante t > t0 . L’evoluzione temporale deve
mantenere l’ortogonalità degli stati , perciò l’evoluzione è data da delle matrici
unitarie Ut (dove t è il tempo) cosicché questa condizione sia soddisfatta. Una matrice
Ut è detta unitaria se soddisfa la condizione Ut∗ = Ut−1 .
L’evoluzione si ottiene applicando Ut allo stato iniziale, per esempio ψt0 , si ha
quindi che lo stato al tempo t è
ψt = Ut ψt0
L’unitarietà implica che l’ortogonalità è conservata, infatti se ϕt0 ⊥ ψt0 =⇒ (ϕt0 , ψt0 ) = 0
si ha
=0
ϕ
ψ
=1
z }| { ev.temporale z }|t { z }|t {
z }| {
(ϕt0 , ψt0 ) =⇒ (Ut ϕt0 , Ut ψt0 ) = (Ut∗ Ut ϕt0 , ψt0 ) = (ϕt0 , ψt0 ) = 0 =⇒ ϕt ⊥ ψt
Nel caso di uno stato misto9 iniziale ρ̂t0 lo stato al tempo t è dato da
ρ̂t = Ut ρˆt0 Ut∗
3.9
Incompatibilità
L’incompatibilità è un fenomeno che riguarda le osservabili. Supposto di avere due osservabili diverse A e B, si dice che l’osservabile A è incompatibile con B quando, in
un’esperienza, si misura dapprima l’osservabile A trovando il valore a, poi quasi simultaneamente si misura un’altra osservabile B trovando che vale b e subito si rimisura A
scoprendo che il suo valore non è più a con certezza, ma può essere per esempio c. Il
processo di misura dell’osservabile B ha quindi influito anche sul risultato della misura
8
9
Ad eccezione del processo di misura che non è deterministico.
ρ̂ è una matrice densità (v.cap 3.4).
3. La struttura della meccanica quantistica
19
dell’altra osservabile A, cambiando lo stato del sistema. Talvolta invece dell’affermazione
“due osservabili sono compatibili” si usa anche dire “due osservabili sono simultaneamente
misurabili”.
Un sistema è detto quantistico se nella sua algebra delle osservabili esistono delle osservabili non compatibili10 , matematicamente si dice che in un sistema quantistico l’algebra
delle osservabili non è commutativa, ovvero date due osservabili non compatibili A e B:
AB 6= BA
Nel sistema spin 21 vedremo per esempio che AB − BA 6= 0 (v.cap. 4.1).
In un sistema classico tutti le osservabili sono compatibili e l’algebra delle osservabili è
commutativa (AB = BA).
3.10
Il Principio di indiscernibilità
Il principio d’indiscernibilità ha un ruolo fondamentale nell’interpretazione del fenomeno
delle interferenze quantistiche. Esso è cosı̀ formulato: “Le interferenze si manifestano
quando una particella può scegliere fra più percorsi per giungere a uno stesso detettore, e
questi percorsi sono indistinguibili (indiscernibili) dopo la sua detezione”.
Per esempio nell’interferometro di Mach-Zehnder (v.cap. 4.2) vedremo che la particella
ha sempre due traiettorie possibili per arrivare a uno dei due rilevatori e che, dopo la
detezione, non è possibile sapere in quale percorso è passata la particella.
3.11
Complementarità
In determinate situazioni due o più informazioni non possono essere conosciute
contemporaneamente. Per esempio nell’interferometro di Mach-Zehnder (v.cap 4.2), il
cammino che ha percorso la particella per arrivare al detettore e il risultato, ovvero l’uscita
presa dalla particella, non possono essere conosciute simultaneamente. Ciò significa che
queste due informazioni sono complementari : o se ne conosce una oppure l’altra.
3.12
Delocalizzazione e non località
Nel caso delle interferenze a una particella si nota che la particella non è
localizzata in un cammino ben preciso, ma è potenzialmente delocalizzata
nei diversi percorsi che giungono allo stesso detettore dell’osservabile (v.cap. 4.2,
interferometro di Mach-Zehnder).
Nelle interferenze a due particelle (nei sistemi composti) le correlazioni che
10
Un sistema è detto quantistico non solamente in questo caso.
3. La struttura della meccanica quantistica
20
possono avvenire anche fra particelle molto distanti tra loro, permettono di affermare
che le correlazioni non sono un effetto locale. Questo significa che la distanza (o
località) fra le particelle non influenza l’attuazione di correlazioni quantistiche (v.cap.
4.4, interferometro di Franson).
Entrambi i fenomeni saranno approfonditi al momento di trattare le rispettive esperienze.
Capitolo 4
Esperienze e fenomeni quantistici
In questo capitolo si applicano le conoscenze acquisite a dei sistemi concreti. Ogni esperienza è dapprima brevemente descritta, poi è presentata la costruzione di un modello
fisico che sia fedele a quello che accade nell’esperimento e infine vengono discussi i
risultati ottenuti in relazione al modello trovato.
4.1
L’esperienza di Stern-Gerlach: il sistema spin
1
2
Riprendiamo ora il problema posto nel capitolo 2.1, analizzandolo dettagliatamente.
Il sistema spin 21 è uno degli esperimenti più significativi degli effetti d’incompatibilità
fra osservabili della meccanica quantistica (v.cap. 3.9).
4.1.1
Descrizione
L’esperienza del sistema spin 12 è costituita dall’apparecchio di Stern-Gerlach. Esso è
formato da una sorgente che emette una sola particella alla volta, più precisamente un
atomo di argento [Ag], due magneti che creano un campo magnetico molto disomogeneo
orientato secondo una certa direzione ~en ∈ R3 stabilita, e una “carta fotografica” che
registra dove arrivano gli atomi (detettore). L’apparecchio di Stern-Gerlach ha come
effetto quello di deviare le particelle in due sole direzioni in funzione dell’orientamento
del suo campo magnetico disomogeneo.
A ogni diverso orientamento ~en dell’apparecchio (e quindi del suo campo magnetico) si
associa un’osservabile notata per convenzione σn , che dev’essere una matrice autoaggiunta (v.cap. 3.2). Per esempio se l’orientamento è secondo il vettore ~e3 , l’osservabile
che verrà presa in considerazione nella misura è σ3 .
Cosa si osserva
1. Dalla sorgente esce una particella, che passando attraverso il campo magnetico fortemente disomogeneo viene deviata in due sole possibili direzioni: verso l’alto (a
21
4.1 L’esperienza di Stern-Gerlach: il sistema spin
1
2
22
cui associamo per convenzione il valore +1) oppure verso il basso (valore −1). L’evoluzione temporale attraverso il campo magnetico disomogeneo dell’apparecchio
non è deterministica, poiché l’apparecchio ha il ruolo di strumento di misura.
Questo comporta l’uso di una descrizione in termini di probabilità oggettive nella
predizione dei risultati dell’esperimento. È importante sottolineare che si predice il
risultato di una misura in modo probabilistico, non perché non siamo in grado di
avere maggiori informazioni sul sistema, bensı̀ perché è la natura stessa del sistema
che si comporta cosı̀.
2. Mettendo in serie tre apparecchi di Stern-Gerlach, il primo con lo stesso orientamento dell’ultimo, dove si misura σ3 , e il secondo con un diverso orientamento, dove
si misura σn , si osserva che le osservabili σ3 e σn sono incompatibili . Per
un’esposizione più semplificata della serie d’osservazioni vedi capitolo 2.1.
Immagini
Figura 4.1: Schematizzazione dell’apparecchio di Stern-Gerlach.
Figura 4.2: Montaggio dell’esperienza di Stern-Gerlach: si notano il campo magnetico
disomogeneo e i due soli risultati della misura (spin up = +1; spin down = −1).
4.1 L’esperienza di Stern-Gerlach: il sistema spin
1
2
23
Figura 4.3: Documento originale della distribuzione degli atomi: a destra con il campo
magnetico disomogeneo, a sinistra senza campo magnetico.
Cenni storici
Quando venne fatta l’esperienza, non si sapeva ancora quali risultati essa avrebbe
dato. Infatti la predizione dei risultati, di tipo classico (a quell’epoca), prevedeva
una distribuzione “a macchia” (v. figura 4.4). Le prime vecchie teorie quantistiche
prevedevano invece che gli atomi si sarebbero concentrati in 3 punti distinti. Si osservò
invece che gli atomi si raggruppavano in due soli punti.
Figura 4.4: Previsione dei risultati dell’esperienza.
4.1.2
Modellizzazione
Passiamo ora alla descrizione matematica del sistema.
Iniziamo con la costruzione delle matrici delle osservabili. I risultati possibili di una misura
sono solamente due (+1 o −1), indipendentemente dall’orientazione dell’apparecchio di
Stern-Gerlach.
Come prima osservabile prendiamo σ3 . Scriviamo esplicitamente i valori che si possono
4.1 L’esperienza di Stern-Gerlach: il sistema spin
osservare sulla diagonale della matrice σ3 . Se tutte
compatibili allora si avrebbe che
1 0 0 0
0 −1 0 0
σ3 =
0 0 1 0
0 0 0 −1
.. .. .. ..
. . . .
1
2
24
le osservabili σn del sistema fossero
···
···
···
···
..
.
L’esperienza mostra invece che non vi sono altre osservabili compatibili, perciò la matrice
si riduce ai due soli valori osservabili in una misura di σ3 , ossia
!
1 0
σ3 =
0 −1
L’algebra delle osservabili è quindi formata da delle matrici autoaggiunte 2 × 2, ossia
A ⊂ M2 (C).
Gli stati (puri) saranno rappresentati da dei vettori dello spazio di Hilbert H = C2 . Questo tipo sistemi sono chiamati sistemi a due livelli .
!
α
Determiniamo gli stati puri associati all’osservabile σ3 . Poniamo ψ+ =
β
!
α0
lo stato puro associato al valore +1 dell’osservabile σ3 e ψ− =
quello associato
β0
al valore −1. Questi due stati puri sono anche, per definizione, due stati di conoscenza
assoluta per l’osservabile σ3 . Le equazioni agli autovalori ci permettono di determinare
ψ+ e ψ− .
Dall’equazione all’autovalore +1 dell’osservabile σ3 si ricava l’autovettore ψ+
normalizzato, ovvero
!
!
!
!
1 0
α
α
1
σ3 ψ+ = 1ψ+ ⇐⇒
=
⇐⇒ ψ+ =
0 −1
β
β
0
e dall’equazione all’autovalore −1 dell’osservabile σ3 si ricava l’autovettore ψ−
normalizzato, ovvero
!
!
!
!
0
0
1 0
α
α
0
σ3 ψ− = −1ψ− ⇐⇒
=
⇐⇒ ψ− =
0
0
0 −1
β
β
1
Disponiamo ora di due stati ortogonali ψ+ e ψ− che formano una base ortonormata
dello spazio di Hilbert H = C2 . Rappresenteremo tutte le altre osservabili ed i
vettori rispetto a questa base.
4.1 L’esperienza di Stern-Gerlach: il sistema spin
1
2
25
Facciamo ora delle esperienze sullo spin 12 preparato nello stato ψ+ 1 . Per preparare il sistema nello stato ψ+ facciamo passare lo spin 12 (dell’atomo di argento)
nell’apparecchio di Stern-Gerlach: se venisse deviato verso l’alto lo stato che descrive il
sistema sarà rappresentato da ψ+ , viceversa se fosse deviato verso il basso lo stato sarà
ψ− (per il Postulato della misura ideale (1), v.cap. 3.7). A questo punto si prende una
particella che è nello stato ψ+ e la si fa passare in un altro apparecchio Stern-Gerlach
dove si misura una nuova osservabile associata alla direzione ~e1 , chiamata σ1 .
L’informazione che ci fornisce l’esperienza è
hσ1 iψ+ = (ψ+ , σ1 ψ+ ) = 0
e
hσ1 iψ− = (ψ− , σ1 ψ− ) = 0
Disponendo di questa informazione possiamo iniziare a cercare la matrice dell’osservabile
σ1 . Sappiamo già che deve essere una matrice autoaggiunta i cui autovalori sono ±1.
Gli elementi di matrice di σ1 rispetto a una base {e1 , e2 } sono σ1ij = (ei , σ1 ej ). Quindi la
matrice σ1 rispetto alla base {e1 = ψ+ , e2 = ψ− } si scrive
σ =(e ,σ e ) σ1 =(e1 ,σ1 e2 )
1
1 1 1
12
z }| {
!
z 11 }| {
(ψ , σ ψ )
−iφ1
−iφ1
ξ
e
0
ξ
e
(dati esperienza)
+
1 +
1
1
=
σ1 =
iφ1
iφ
1
ξ1 e
(ψ− , σ1 ψ− )
ξ1 e
0
| {z }
| {z }
σ121 =(e2 ,σ1 e1 )
σ122 =(e2 ,σ1 e2 )
√
con ξ1 ∈ R+ , i = −1 e φ1 ∈ [0, 2π]. ξ1 eiφ1 è un modo generale di rappresentare un
numero complesso. Il fatto che σ121 = ξ1 eiφ1 diventi ξ1 e−iφ1 = σ112 è per far sı̀ che la
matrice σ1 sia autoaggiunta, ossia σ1∗ = σ1 .
Ora cerchiamo i valori da attribuire a ξ1 e φ1 . Sfruttiamo l’invarianza del determinante
della matrice σ1 rispetto al cambiamento di base. Notiamo σe1 la matrice dell’osservabile σ1
nella base dei suoi autovettori {ϕ+ , ϕ− } anziché la base {ψ+ , ψ− } scelta precedentemente.
È come se avessimo scelto ϕ+ e ϕ− come primi vettori che formavano la base di !
C2 con
1 0
cui esprimere tutti le altre osservabili. Si avrebbe allora avuto che σe1 =
il cui
0 −1
determinante è
det σe1 = 1 · (−1) − 0 · 0 = −1
Il determinante di σ1 è invece det σ1 = 0 · 0 − ξ1 e−iφ1 · ξ1 eiφ1 = −ξ12 .
Per invarianza del determinate di una matrice (σ1 ) rispetto a cambiamenti di base si ha
det σe1 = det σ1 ⇐⇒ −1 = −ξ12 ⇐⇒ ξ1 = ±1
Per comodità si sceglie ξ1 = 1. Per quanto riguarda φ1 si può imporre per semplificare
φ1 = 0. Abbiamo cosı̀ determinato la matrice autoaggiunta dell’osservabile associato alla
direzione ~e1 , ossia
!
0 1
σ1 =
1 0
1
Equivalentemente si procede nell’esperienza preparando il sistema nello stato ψ− .
4.1 L’esperienza di Stern-Gerlach: il sistema spin
1
2
26
Ripetiamo ora il ragionamento compiuto per trovare gli autovettori ψ+ e ψ− di σ3 . Sappiamo che ϕ+ e ϕ− sono due stati puri e sono anche, per definizione, due stati di conoscenza
assoluta per l’osservabile σ1 , perciò devono essere gli autovettori di σ1 , ossia devono soddisfare l’equazione agli autovalori +1 e −1. Dall’equazione all’autovalore +1 dell’osservabile
σ1 si ricava l’autovettore ψ+ normalizzato:
!
!
!
!
1
0 1
α
α
1
σ1 ϕ+ = +1ϕ+ ⇐⇒
=
⇐⇒ ϕ+ = √
1 0
β
β
2 1
L’autovettore ϕ− associato all’autovalore −1 lo si trova dalla rispettiva equazione
all’autovalore −1:
!
!
!
!
1
0 1
α
α
1
σ1 ϕ− = −1ϕ− ⇐⇒
=
⇐⇒ ϕ− = √
1 0
β
β
2 −1
È facile notare che ϕ+ e ϕ− sono ortogonali.
L’osservabile σ2 , associato alla direzione ~e2 nello spazio, si trova procedendo in modo
analogo al procedimento appena presentato per σ1 .
L’esperienza mostra che
hσ2 iψ+ = (ψ+ , σ2 ψ+ ) = 0
hσ2 iψ− = (ψ− , σ2 ψ− ) = 0
e
La matrice σ2 rispetto alla base {ψ+ , ψ− } si scrive
!
(ψ+ , σ2 ψ+ )
ξ2 e−iφ2
(dati esperienza)
=
σ2ij = (ei , σ2 ej ) =
iφ2
ξ2 e
(ψ− , σ2 ψ− )
0
ξ2 e−iφ2
ξ2 eiφ2
0
!
con ξ2 ∈ R+ e φ2 ∈ [0, 2π]. Come per ξ1 (sfruttando quindi l’invarianza del determinate
rispetto ai cambiamenti di base), possiamo fissare ξ2 = 1. In questo caso non possiamo
porre φ2 = 0, altrimenti avremmo la stessa matrice di σ1 e quindi anche la stessa osservabile. Per determinare φ2 si prepara il sistema nello stato ϕ− e dall’esperienza si ricava
che hσ2 iϕ− = 0. Calcolando esplicitamente questo valore medio si ha
0 = hσ2 iϕ− = (ϕ− , σ2 ϕ− ) =
da cui φ2 ∈ { π2 , 3π
}. Quindi scegliendo φ2 =
2
σ2 =
e−iφ2 + eiφ2
= cos φ2
2
π
2
abbiamo
!
0 −i
i 0
Gli autovettori di σ2 , che chiamiamo χ+ e χ− , si ricavano, compiendo lo stesso ragionamento precedente per determinare gli autovettori di σ1 e σ3 , dalle equazioni agli
autovalori
σ2 χ+ = +1χ+
e
σ2 χ− = −1χ−
4.1 L’esperienza di Stern-Gerlach: il sistema spin
da cui
1
χ+ = √
2
1
i
!
e
1
2
27
1
χ− = √
2
1
−i
!
Qui si vede la necessità di descrivere l’algebra delle osservabili con delle
matrici a coefficienti complessi e di quindi costruire la meccanica quantistica
non su uno spazio vettoriale reale, bensı̀ complesso.
4.1.3
Riepilogo
Riassumo gli elementi più importanti del sistema che conosciamo ora:
• Le matrici autoaggiunte che rappresentano le tre osservabili σ1 , σ2 e σ3 ;
• Due stati puri e di conoscenza assoluta per l’osservabile σ3 : ψ+ e ψ− ;
• Quattro stati puri, ma non di conoscenza assoluta per l’osservabile σ3 : ϕ+ , ϕ− , χ+
e χ− ;
• Quattro stati (puri) di superposizione degli stati propri ψ+ e ψ− , per esempio:
ϕ+ =
√1 ψ+
2
+
√1 ψ−
2
ovvero ϕ+ è uno stato di superposizione di ψ+ e ψ− .
ϕ− =
√1 ψ+
2
−
√1 ψ−
2
ovvero ϕ− è uno stato di superposizione di ψ+ e ψ− .
• Gli stati misti del sistema sono rappresentati da combinazioni lineari convesse di
stati puri, per esempio la matrice densità 2 (α ∈]0, 1[)
!
!
!
1 0
0 0
α
0
+ (1 − α)
=
ρ̂ = αPψ+ + (1 − α)Pψ− = α
0 0
0 1
0 1−α
rappresenta uno stato misto del sistema, in cui si sa che il sistema è nello stato puro
ψ+ con probabilità α oppure nello stato puro ψ− con probabilità (1 − α).
È interessante notare la differenza tra questo stato misto ed il proiettore associato
a uno stato puro di superposizione ψ del sistema
!
√
√
√
α
ψ = αψ+ + 1 − αeiθ ψ− ⇐⇒ ψ = √
1 − α eiθ
=⇒ Pψ =
2
α
p
α(1 − α)e−iθ
p
α(1 − α)eiθ
1−α
!
6=
Nell’appendice B sono elencate le formule principali usate in questo testo.
α
0
0 1−α
!
= ρ̂
4.1 L’esperienza di Stern-Gerlach: il sistema spin
4.1.4
1
2
28
Discussione
Grazie alla modellizzazione si hanno i mezzi necessari per calcolare oggettivamente
le probabilità di osservare gli autovalori delle osservabili, sfruttando le regole di calcolo
delle probabilità illustrate nel capitolo 3.6.
1. Prima esperienza
Consideriamo l’esperimento schematizzato nella figura 4.5.
Ci sono due apparecchi di Stern-Gerlach che misurano entrambi l’osservabile σ3 .
Figura 4.5: Primo esperimento di Stern-Gerlach.
La particella parte da sinistra, in alto, entra nel primo apparecchio e viene deviata verso
destra. Per il postulato della misura ideale (1) (v.cap. 3.7), il sistema a questo momento
è nello stato ψ+ . In seguito la particella raggiunge il secondo apparecchio (con lo stesso
orientamento del primo). A questo punto possiamo calcolare le probabilità dei risultati,
ovvero:
• probabilità che la particella venga deviata verso l’alto (autovalore +1) è
Probψ+ {σ3 = +1} = ||Pψ+ ψ+ ||2 = ||(ψ+ , ψ+ )ψ+ ||2 = | (ψ+ , ψ+ ) |2 ||ψ+ ||
| {z } | {z }
=||ψ+ ||2 =1
2
=1
=1
• probabilità che la particella venga deviata verso il basso (autovalore −1) è
Probψ+ {σ3 = −1} = ||Pψ− ψ+ ||2 = ||(ψ− , ψ+ )ψ− ||2 = | (ψ− , ψ+ ) |2 ||ψ− ||
| {z } | {z }
=0 [ψ+ ⊥ψ− ]
2
=0
=1
Gli stati propri ψ+ e ψ− sono stati di conoscenza assoluta (per σ3 ): infatti tutte le
particelle in questo caso saranno deviate verso l’alto (stato ψ+ ), con probabilità 1, e
nessuna verso il basso (stato ψ− ).
2. Seconda esperienza
Mettiamo ora in serie tre apparecchi di Stern-Gerlach, come indicato nella Figura 4.6.
Il primo apparecchio è identico all’ultimo, quindi con lo stesso orientamento (e~3 ), mentre
quello centrale ha un diverso orientamento (e~1 ).
4.1 L’esperienza di Stern-Gerlach: il sistema spin
1
2
29
Figura 4.6: Secondo esperimento di Stern-Gerlach.
La particella parte da sinistra, in alto, entra nel primo apparecchio orientato secondo il
vettore ~e3 e viene deviata verso destra. Per il postulato della misura ideale (1) (v.cap.
3.7), il sistema è a questo istante nello stato ψ+ . In seguito la particella raggiunge il
secondo apparecchio, orientato secondo il vettore ~e1 . A questo punto possiamo calcolare
la probabilità di osservare i valori dell’osservabile σ1 , ovvero:
• probabilità che la particella venga deviata verso l’alto (autovalore +1) è
Probψ+ {σ1 = +1} = ||Pϕ+ ψ+ ||2 = ||(ϕ+ , ψ+ )ϕ+ ||2 = |(ϕ+ , ψ+ )|2 ||ϕ+ ||
| {z }
2
=1
= |(ϕ+ , ψ+ )|2 = | √12 1 +
√1 0|2
2
= | √12 |2 =
1
2
• probabilità che la particella venga deviata verso il basso (autovalore −1) è
Probψ+ {σ1 = −1} = ||Pϕ− ψ+ ||2 = ||(ϕ− , ψ+ )ϕ− ||2 = |(ϕ− , ψ+ )|2 ||ϕ− ||
| {z }
2
=1
= |(ϕ− , ψ+ )|2 = | √12 0 −
√1 1|2
2
=|−
√1 |2
2
=
1
2
Dunque la particella ha il 50% di possibilità di essere deviata verso l’alto e in questo caso
dopo la misura è nello stato ϕ+ . Al 50% essa è deviata verso il basso, che corrisponde
allo stato ϕ− . Adesso ci concentriamo sulla particella che viene deviata verso l’alto. Essa
si trova nello stato ϕ+ , che è uno stato di superposizione di ψ+ e ψ− . Quando entra nel
terzo apparecchio di Stern-Gerlach, orientato come il primo secondo la direzione ~e3 , le
probabilità di osservare ±1 nella misura di σ3 sono date da
• probabilità che la particella venga deviata verso l’alto (autovalore +1) è
Probϕ+ {σ3 = +1} = ||Pψ+ ϕ+ ||2 = |(ψ+ , ϕ+ )|2 ||ψ+ ||2 = |(ψ+ , ϕ+ )|2 =
1
2
4.1 L’esperienza di Stern-Gerlach: il sistema spin
1
2
30
• probabilità che la particella venga deviata verso il basso (autovalore −1) è
Probϕ+ {σ3 = −1} = ||Pψ− ϕ+ ||2 = |(ψ− , ϕ+ )|2 ||ψ− ||2 = |(ψ− , ϕ+ )|2 =
1
2
Facendo passare un gran numero di particelle, si constata che tutte queste
probabilità sono confermate dai risultati sperimentali. Perciò questo sistema mostra un caso di incompatibilità di osservabili, in cui la misura del
valore dell’osservabile σ1 perturba lo stato del sistema, modificando (nella metà dei casi) il valore dell’altra osservabile σ3 precedentemente misurato.
Matematicamente l’incompatibilità si manifesta con la non commutatività delle
matrici delle osservabili σ1 e σ3 :
σ3 σ1 6= σ1 σ3
Infatti
[σ1 , σ3 ] = σ1 σ3 − σ3 σ1 = −2iσ2 6= 0
4.1.5
Conclusioni
• L’apparecchio di Stern-Gerlach devia le particelle solamente in due direzioni in
funzione dell’orientamento del gradiente del campo magnetico.
• Quando le particelle attraversano successivamente tre campi magnetici orientati
secondo ~e3 , ~e1 e ~e3 la deviazione delle particelle all’uscita del terzo campo magnetico
è prodotta in due direzioni possibili, invece di una sola prevista se le osservabili σ3
e σ1 fossero compatibili.
• Il secondo apparecchio di Stern-Gerlach modifica lo stato delle particelle, influenzando il risultato della misura del primo osservabile (σ3 ), portando cosı̀ a delle
osservabili incompatibili fra loro.
• In riferimento al quesito del capitolo 2.1, possiamo quindi affermare che ogni biglia
(particella) esce dal secondo apparecchio di misura (σ1 ) metà gialla e metà celeste
(ovvero nello stato di superposizione ϕ+ ).
4.1.6
Complemento: una nuova proprietà dell’elettrone, lo spin
Esiste una corrispondenza biunivoca tra gli stati puri ψ ∈ C2 dello spin
~n ∈ R3 .
~n ∈ R3
ψ~n ∈ C2
1
2
e i vettori
Si dice quindi che lo spin è nella direzione ~n se lo stato (puro) in cui è la
particella corrisponde al vettore ψ~n associato a questa direzione. La direzione
~n equivale pure all’orientamento dell’apparecchio di Stern-Gerlach. Per esempio se la
4.1 L’esperienza di Stern-Gerlach: il sistema spin
1
2
31
particella è nello stato ψ+ , allora lo spin è nella direzione ~e3 , e se è nello stato ψ− lo spin
è nella direzione −~e3 , ecc.
Le componenti ni del vettore ~n in funzione di quelle dello stato ψ del sistema sono date
da [2]
ni = (ψ, σi ψ)
Calcolando esplicitamente il prodotto scalare si ottiene
n1 = ψ̄1 ψ2 + ψ1 ψ̄2
n2 = −i(ψ̄1 ψ2 − ψ1 ψ̄2 )
n3 = |ψ1 |2 − |ψ2 |2
(4.1)
Si verifica che il vettore ~n è normalizzato (||~n|| = 1).
Cerchiamo ora le componenti ψ1 e ψ2 del vettore ψ~n (normalizzato) in funzione del vettore
~n = (n1 , n2 , n3 ) ∈ R3 le cui componenti ni sono espresse mediante le coordinate sferiche
(θ, ϕ)
n1 = sin θ cos ϕ
(4.2)
n2 = sin θ sin ϕ
n3 = cos θ
con θ ∈ [0, π[ e ϕ ∈ [0, 2π[.
Eguagliando le componenti di ~n espresse in coordinate sferiche (4.1) a quelle espresse in
funzione delle componenti del vettore ψ~n (4.2), e risolvendo rispetto a ψ1 e ψ2 si ottiene
[2]
!
!
ψ1
cos 2θ e−iϕ/2
ψ~n =
=
sin 2θ eiϕ/2
ψ2
Questo risultato permette di caratterizzare lo spin: lo spin 12 è una proprietà di
una particella legata ad un orientamento nello spazio R3 . Più precisamente, nel
nostro caso, è il momento cinetico intrinseco dell’elettrone dell’ultimo guscio dell’atomo
di argento. Esso può prendere solo due valori.
Fu cosı̀ scoperta, nel 1925, una nuova proprietà (osservabile) degli elettroni, che descrive
la loro interazione con un campo magnetico. L’elettrone è quindi ora caratterizzato da
~ = ~ ~σ , dove ~ è la
tre grandezze intrinseche: la massa (me ), la carica (−e) e lo spin S
2
costante di Planck introdotta per delle questioni di dimensioni. Quindi per esempio
l’osservabile σ3 può prendere solo i valori ± 12 ~.
4.1.7
Complemento: l’evoluzione temporale dello spin in un
campo magnetico omogeneo
Nell’esperienza è stato trattato l’apparecchio di Stern-Gerlach, in cui la particella (ossia
l’elettrone dell’ultimo guscio dell’atomo di Ag) interagisce con il campo magnetico
(molto) disomogeneo. Vediamo ora cosa succede allo spin se si trovasse in un campo
~ orientato secondo la direzione ~e3 .
omogeneo B
4.1 L’esperienza di Stern-Gerlach: il sistema spin
1
2
32
Dal capitolo 3.8 sappiamo che l’evoluzione temporale degli stati del sistema è data da
delle matrici unitarie Ut . Nel nostro caso t è il tempo che impiega la particella per
~
attraversare il campo magnetico B.
Passiamo ora all’evoluzione degli stati puri del sistema, che è data da
ψt = Ut ψ0
~ e ψ0 è lo stato puro iniziale (prima di B).
~
dove ψt è lo stato puro al tempo t (dopo B)
La matrice di evoluzione è data da [2]
i
Ut = e− ~ Ht
~ = B~e3 l’energia d’interazione spin –
Per uno spin 21 in un campo magnetico omogeneo B
campo magnetico vale3 −γB ~2 σ3 . Quindi l’osservabile che rappresenta l’energia è
!
−γB ~2
0
~
H = −γB σ3 =
2
0
γB ~2
e
i
− Ht =
~
i
γB ~2 t
~
0
0
i
− ~ γB ~2 t
!
iγ B2 t
0
0
−iγ B2 t
=
!
Ora, per una matrice diagonale A (di elementi aij ) l’esponenziale di A, ossia la matrice
eA , ha i seguenti elementi eaij δij , applicando questa regola all’operatore di evoluzione
otteniamo quindi
!
iγ B
t
2
e
0
Ut =
−iγ B
0
e 2t
Gli stati puri finali sono dati da4
B
ψt = Ut ψ0 =
eiγ 2 t
0
−iγ B
0
e 2t
!
cos 2θ e−iϕ/2
sin 2θ eiϕ/2
!
=
cos 2θ e−i(−γBt+ϕ)/2
sin 2θ e−i(−γBt+ϕ)/2
!
Le componenti, espresse in coordinate sferiche, del vettore5 ~n(t) in funzione del tempo t
associato allo stato ψt sono date da6 ni = hσi iψt , quindi
sin θ cos(−γBt + ϕ)
~n(t) = sin θ sin(−γBt + ϕ)
cos θ
e
Vedi [2], γ si chiama fattore giromagnetico e vale γ = 2g m
(con e > 0) dove g è il rapporto giromagnetico, il cui valore dipende dalla struttura interna della particella, per esempio
gelettrone = −2.0024 ; gneutrone = −3.8256 .
4
ψ0 è espresso in funzione delle coordinate sferiche di ~n, vedi capitolo 4.1.6.
5
Vedi sezione precedente.
6
Poiché ~n(t) = (ψt , ~σ ψt ).
3
4.1 L’esperienza di Stern-Gerlach: il sistema spin
1
2
33
Il vettore ~n(t) gira sempre attorno all’asse ~e3 del campo magnetico. Per esempio, ponendo
per semplificare la situazione θ = π2 e ϕ = 0, si ha che lo stato iniziale prima del campo
magnetico ψ0 ∈ C2 associato al vettore iniziale ~n(0) ∈ R3 è
!
√ !
sin π2 cos 0
1
2
π
cos
4
√2
=
~n(0) = sin π2 cos π2 = 0
ψ0 =
2
sin π4
2
cos π2
0
L’evoluzione dello stato ψ0 nel campo magnetico omogeneo, in funzione del tempo t che
la particella impiega ad attraversarlo, è
!
!
√
i
2 2i γBt
e
cos π4 e 2 γBt
√2
ψt = Ut ψ0 =
=
i
2 2i γBt
sin π4 e 2 γBt
e
2
il vettore ~n(t) associato allo stato ψt è
sin π2 cos(−γBt)
cos(−γBt)
~n(t) = sin π2 sin(−γBt) = sin(−γBt)
0
cos π2
Se regoliamo il campo magnetico in modo che il vettore ~n(t) compia una rotazione di 2π,
ossia
γBt = 2π
Abbiamo quindi che il vettore ~n(t) all’istante t1 =
2π
γB
è
1
cos 2π
~n(t1 ) = − sin 2π = 0 = ~n(0)
0
0
e lo stato ψt1 della particella associato a questo vettore ~n è
!
!
!
√
√
√
2 2i 2π
2 iπ
2
e
e
(−1)
√2
√2
√2
ψt1 =
=
=
= −ψ0
2 2i 2π
2 iπ
2
e
e
(−1)
2
2
2
Quindi il vettore ~n (e quindi anche lo spin) con una rotazione di 2π ritorna
nella direzione iniziale, ma lo stato della particella non è quello iniziale.
Se invece ora regoliamo il campo magnetico in modo che il vettore ~n(t) compia una
rotazione di 4π, ossia
γBt = 4π
Abbiamo quindi che il vettore ~n(t) all’istante t2 =
4π
γB
è
cos 4π
1
~n(t2 ) = − sin 4π = 0 = ~n(0)
0
0
4.1 L’esperienza di Stern-Gerlach: il sistema spin
1
2
34
e lo stato ψt2 della particella associato a questo vettore ~n è
!
!
!
√
√
√
2 2i 4π
2 i2π
2
e
e
1
√2
√2
√2
ψt2 =
= ψ0
=
=
2 2i 4π
2 i2π
2
e
e
1
2
2
2
Quindi il vettore ~n (e quindi anche lo spin) con una rotazione di 4π ritorna
nella direzione iniziale e pure lo stato della particella ritorna a essere
quello iniziale.
Dagli esempi precedenti vediamo che lo spin gira attorno all’asse del campo
magnetico (~e3 ) con velocità angolare ω0 = −γB. Per un certo valore di B e del tempo
t, lo spin (vettore ~n) ritorna al punto di partenza (giro completo, ossia γBt = 2π), ma
lo stato del sistema per questo valore è −ψ. Se lo spin compie una rotazione di 4π,
ossia due giri attorno all’asse del campo magnetico, allora lo stato del sistema ritorna ad
essere ψ. Gli stati ψ e −ψ sono equivalenti, ma il cambio di segno ha delle conseguenze
importanti nella superposizione di stati, come vedremo più avanti nell’esperienza di
Rauch (v.cap. 4.3).
~ sullo spin della particella sono riassunte in questa
Le informazioni dell’azione di B
tabella. Si supponga che ~n sia la direzione dello spin iniziale (prima di entrare nel campo)
e ψ il suo stato iniziale.
~
Rotazione indotta da B
0π
2π
4π
Spin
~n → ~n
~n → ~n
~n → ~n
Stato
ψ→ψ
ψ → −ψ
ψ→ψ
~
Tabella 4.1: Informazioni sull’azione di B.
La velocità angolare ω0 di ~n è data da
ω0 = −γB
nel nostro caso γ = γelettrone = − mee .
Dal tempo t impiegato dalla particelle per attraversare il campo possiamo trovare ω0 , per
ottenere una certa rotazione ϕ dello spin: ϕ = ω0 t. Per esempio se lo spin viene ruotato
di 2π si ha ω0 = 2πt .
~ in modo da ottenere una delle rotazioni desiderate,
A questo punto si sceglie B
nell’esempio di prima B = − ωγ0 = − 2π
.
γt
4.2 L’interferometro di Mach-Zehnder
4.2
35
L’interferometro di Mach-Zehnder
Riprendiamo ora il problema posto nel capitolo 2.2, studiandolo dettagliatamente.
Il sistema presenta uno degli esperimenti più significativi degli effetti d’interferenza
quantistica ad una particella.
4.2.1
Descrizione
L’intereferometro di Mach-Zehnder è formato da cinque elementi: una sorgente che
emette una particella alla volta, due separatori di fascio semitrasparenti (detti Beam
Splitter, o BS), due specchi che deviano la direzione di propagazione delle particelle,
due detettori e un “differenziatore” di cammino (v. figure 4.7 e 4.8). Le particelle che
fuoriescono dalla sorgente sono microscopiche, per esempio fotoni o neutroni. Nella figura
4.7 è illustrato lo schizzo dell’esperienza.
Figura 4.7: Primo esperimento di Mach-Zehnder.
Cosa si osserva
Si fanno passare attraverso l’interferometro molte particelle.
Si sa che i beam
splitter sono equilibrati, ovvero che una particella che arriva ha il 50% di possibilità di
continuare diritto e il 50% di essere deviata verso il basso. Intuitivamente si direbbe
quindi che alla fine la metà delle particelle emesse saranno giunte nel detettore D1 e
l’altra metà nel detettore D2 (v.cap. 2.2). L’esperienza mette invece in risalto la falsità
della nostra predizione: tutte le particelle sono state rilevate in D1 e nessuna in D2. Lo
stesso risultato si presenta anche ripetendo l’esperienza più volte.
Visto che sono passate parecchie particelle attraverso l’interferometro, possiamo affermare (classicamente) che sicuramente alcune saranno passate dal cammino A e altre
4.2 L’interferometro di Mach-Zehnder
36
dal cammino B per arrivare al BS2. A questo punto ripetiamo l’esperienza ma con una
variante: introduciamo un allungamento opportuno del percorso (notato φ) sul cammino
B, come mostrato nella figura 4.8. Ecco i risultati dell’esperienza: tutte le particelle sono
state rilevate in D2 e nessuna in D1. Ci troviamo esattamente nella situazione opposta a
quella precedente (senza l’allungamento). Eppure abbiamo introdotto la modifica su un
solo cammino (B) e quindi almeno le particelle che nella prima esperienza dovrebbero
essere passate dal cammino A per giungere al detettore D1 non dovrebbero essere state
influenzate dalla modifica inserita in B, ovvero ci aspettavamo almeno qualche particella
anche in D1. Visto che nell’interferometro ci passa una sola particella alla volta possiamo
anche escludere che ciò sia dovuto a un effetto collettivo di urti o altro.
Si deve perciò constatare che la modifica su B ha influito anche sul cammino
A. Grazie alla modellizzazione si comprenderà come interpretare questo interessante
risultato.
Figura 4.8: Secondo esperimento di Mach-Zehnder: da notare che con l’allungamento di
percorso φ i risultati dell’esperienza si invertono.
4.2.2
Modellizzazione
Anche in questo caso ci troviamo di fronte a un sistema a due livelli . I risultati
possibili della misura con i detettori sono due: la particella è rilevata (a cui attribuiamo
il valore 1) oppure no (valore 0).
L’algebra delle osservabili è formata quindi da delle matrici autoaggiunte 2 × 2, ossia
A ⊂ M2 (C).
Visto che a ogni detettore si associano due numeri (0 o 1), le matrici delle osservabili sono
!
!
1 0
0 0
D2:
X=
e
D1:
Y =
0 0
0 1
4.2 L’interferometro di Mach-Zehnder
37
dove X è la matrice che rappresenta l’osservabile riferito all’apparecchio di misura D2
che rileva la propagazione nella direzione ~x, e Y la matrice che rappresenta l’osservabile
riferito all’apparecchio di misura D1 che rileva la propagazione nella direzione ~y .
2
Gli stati puri sono
! rappresentati da dei vettori dello spazio di Hilbert H = C . Gli stati
α
puri ψi =
del sistema si trovano grazie alle rispettive equazioni agli autovalori 1
β
e 0. Sappiamo, per esempio, che ψx è uno stato di conoscenza assoluta sia per X che per
Y , poiché la detezione di D2 implica la non detezione di D1, quindi7
!
Xψx = 1ψx ⇐⇒
1 0
0 0
!
Y ψx = 0ψx ⇐⇒
0 0
0 1
α
β
!
α
β
!
1
0
!
α
β
!
α
β
!
0
1
!
!
=1
α
β
!
=0
α
β
!
=0
α
β
!
=1
α
β
Da cui segue che
ψx =
α
β
!
=
Analogamente si trova ψy
!
Xψy = 0ψy ⇐⇒
1 0
0 0
!
Y ψy = 1ψy ⇐⇒
0 0
0 1
Da cui segue che
ψy =
ψx =
1
0
α
β
!
=
!
e
ψy =
0
1
!
Lo stato iniziale (prima del BS1) è ψin = ψx , poiché la particella si sposta nella direzione ~x.
Lo stato dopo il BS1, come anche quello finale, è in generale uno stato di
superposizione degli stati ψx e ψy , del tipo
ψout = αψx + βψy
con α, β ∈ C e |α|2 + |β|2 = 1 (normalizzazione)
Dato uno stato di superposizione ψout le probabilità (oggettive) di osservare un autovalore
dell’osservabile X (oppure Y) in una misura sono8
7
8
Il procedimento per trovare gli stati è analogo a quello seguito nel capitolo 4.1.2.
Importante notare che la detezione di un detettore implica la non detezione dell’altro.
4.2 L’interferometro di Mach-Zehnder
38
• Probψout {X = 1} = Probψout {Y = 0} = ||Pψx ψout ||2 = ||(ψx , ψout )ψx ||2
=1
z }| {
= |(ψx , ψout )|2 ||ψx || 2 = |(ψx , ψout )|2 = |1α + 0β|2 = |α|2
• Probψout {Y = 1} = Probψout {X = 0} = ||Pψy ψout ||2 = ||(ψy , ψout )ψy ||2
=1
z }| {
= |(ψy , ψout )| ||ψy ||
2
2
= |(ψy , ψout )|2 = |0α + 1β|2 = |β|2
La somma di tutte le probabilità deve essere ovviamente uguale a 1 (100%). Quindi si vede
la necessità di avere dei vettori normalizzati (||ψout || = 1), infatti la norma di ψout corrip
√
sponde proprio alla somma delle probalilità (cioé 1): ||ψout || = |α|2 + |β|2 = 1 = 1.
Per avere tutte le informazioni sul sistema è ancora necessario sapere come i tre
elementi presenti nell’interferometro (beam splitter, specchi e allungamento) agiscono
sullo stato della particella. Nel capitolo 3.8 abbiamo visto che l’evoluzione temporale
è conosciuta grazie a delle matrici unitarie U , che devono soddisfare, come visto nel
cap.3.8, la condizione U ∗ = U −1 (cosicché, per esempio, ψx e ψy restino ortogonali in
tutto il sistema, ossia durante l’evoluzione).
Il beam splitter
Costruiamo ora la matrice unitaria UBS che descrive l’evoluzione data dal BS. Chiamiamo
t la probabilità di trasmissione, ovvero che la particella non venga deviata dal BS, r
la probabilità di riflessione, ossia che la particella venga deviata dal BS. Ovviamente
deve valere t + r = 1. Abbiamo visto che lo stato iniziale ψin prima del BS è ψx , e lo
stato dopo il BS è ψout = αψx + βψy . Quindi, ricordando che |α|2 è la probabilità di
trasmissione e |β|2 quella di riflessione, si ha
|α|2 = t ⇐⇒ |α| =
√
t
|β|2 = r ⇐⇒ |β| =
e
√
√
Quindi α = |α| eiφ1 = t eiφ1 e β = |β| eiφ2 = r eiφ2
Sostituendo i valori di α e β si ottiene
ψout =
√
t eiφ1 ψx +
⇐⇒ e−iφ1 ψout =
√
tψx +
√
√
r
con φ1 , φ2 ∈ [0, 2π].
r eiφ2 ψy
√
r eiφ2 e−iφ1 ψy
Ponendo eiφ = ei(φ2 −φ1 ) e sapendo che ψout e e−iφ1 ψout descrivono lo stesso stato, poichè
sono linearmente dipendenti ed entrambi normati, si ha
ψout =
√
tψx +
√
r eiφ ψy
=1
{
√ 2 z }|
iφ 2 √ 2
2
Ricordiamo che ||ψout || = | t| + |e | | r| = t + r = 1 (indipendentemente dal fattore
eiφ ).
4.2 L’interferometro di Mach-Zehnder
39
La matrice unitaria che ci dà l’evoluzione è del tipo
!
a b
UBS =
c d
Nel capitolo 3.8 abbiamo visto che
ψout = UBS ψin
√
√
Quindi sapendo che ψin = ψx e che ψout = t ψx + r eiφ ψy si ha
!
!
!
!
√
√ iφ 0
a b
1
1
UBS ψin = ψout ⇐⇒
= t
+ re
1
c d
0
0
!
!
!
!
√ !
√
a
t
0
t
a
⇐⇒
=
+ √ iφ
⇐⇒
= √ iφ
c
0
re
re
c
)
(
√
a= t
⇐⇒
√
c = r eiφ
Sappiamo che UBS dev’essere unitaria perciò
!
ā
c̄
−1
∗
UBS
= UBS
⇐⇒
=
b̄ d¯
d −b
−c a
!
1
det(UBS )
Ponendo9 det(UBS ) = ad − bc = 1, si ha che
ā
=
d
(
)
√
√
c̄ = −b
d = ā = t = t
=⇒
√ iφ
√ −iφ
b̄
=
−c
b
=
−c̄
=
−
r
e
=
−
re
¯
d=a
Inserendo i risultati ottenuti, abbiamo adesso la matrice
!
√
√
t
− r e−iφ
√
UBS = √ iφ
re
t
Si può quindi calcolare
det(UBS ) =
√√
√
√
t t − (− r)e−iφ reiφ = t + r
Vediamo che il valore del det(UBS ) = 1 ipotizzato prima ha senso poiché abbiamo visto
precedentemente che t + r = 1.
Infine per semplificare poniamo φ = π2 , cosicché eiπ/2 = cos π2 + i sin π2 = i e e−iπ/2 =
cos π2 − i sin π2 = −i.
Quindi la matrice che descrive l’evoluzione del sistema dopo il BS è
!
√
√
t
i 1−t
√
√
UBS (t) =
i 1−t
t
9
Fra breve si giustificherà la scelta di det(UBS ) = 1.
4.2 L’interferometro di Mach-Zehnder
40
Gli specchi sono un caso particolare di BS in cui r = 1 (e t = 0).
La modifica di un cammino
Quest’ultima non cambia la direzione di propagazione delle particelle, quindi lo stato
rimane lo stesso (ψout sarà linearmente dipendente a ψin ). Matematicamente
ψout = eiφ ψin
dove eiφ è chiamato fattore di fase. Calcoliamo la matrice U che dà questa evoluzione.
Se ψin = ψx si deve quindi avere
!
!
!
(
)
iφ
iφ
e
a b
1
a=e
ψout = U ψin ⇐⇒ eiφ ψx = U ψx ⇐⇒
=
⇐⇒
0
c d
0
c=0
Visto che U deve essere unitaria, deve valere
!
a c
U ∗ = U −1 ⇐⇒
=
b d
d −b
−c a
!
1
det(U )
dove det(U ) = ad − bc = eiφ d. Quindi
)
(
a = eiφd d ⇐⇒ e−iφ = e−iφ ⇐⇒ d ∈ C∗
c = − eiφb d ⇐⇒ b = 0
Nel caso in cui ψin = ψy l’allungamento non ha alcun effetto, deve perciò valere
!
!
!
(
)
a b
0
0
b=0
U ψy = ψy ⇐⇒
=
⇐⇒
c d
1
1
d=1
La matrice U (φ) che descrive la modifica del cammino B è quindi
!
eiφ 0
U (φ) =
0 1
4.2.3
Riepilogo
• Lo stato finale ψout dopo aver attraversato l’interferometro è quindi10 :
BS2
BS1
}|
}|
F ase z
{ zSpecchio
{
}| { z }| {
1
1
U = UBS
UBS (0) U (φ) UBS
2
2
z
ψout = U ψin
con
Calcoliamo U a tappe:
√
UBS
10
1
2
UBS (0) =
√ !
t i r
√
√
i r
t
0 i
i 0
!
=
√ !
√
ii r i t
√
=
√
i t ii r
Si suppone che i beam splitter siano equilibrati, ossia t = r = 21 .
√ !
√
− r i t
√
√
i t − r
4.2 L’interferometro di Mach-Zehnder
UBS
1
2
√ !
√
− r i t
√
√
i t − r
UBS (0) U (φ) =
!
eiφ 0
0 1
=
√ !
√
−eiφ r i t
√
√
ieiφ t − r
√ !
√
√
√ !
−eiφ r i t
t i r
√
√
=
√
√
2
2
t
ieiφ t − r
i r
!
!
√√
√
√ √
√ √
√ √
− rt(eiφ + 1)
−ieiφ r + it
−eiφ r t + ii r t −ieiφ r r + i t t
√√
√√
√
=
√ √
√ √
iieiφ t r − r t
ieiφ t t − i r r
ieiφ t − ir
− rt(eiφ + 1)
UBS
=
41
1
UBS (0) U (φ) UBS
1
Visto che i BS sono equilibrati, t = r = 12 , si ottiene
U=
− 21 (eiφ + 1) 2i (1 − eiφ )
− 2i (1 − eiφ ) − 21 (eiφ + 1)
!
1 + eiφ −i(1 − eiφ )
i(1 − eiφ )
1 + eiφ
1
=−
2
!
Quindi
ψout
1 + eiφ −i(1 − eiφ )
i(1 − eiφ )
1 + eiφ
1
= U ψx = −
2
!
1
0
!
=
− 12 (eiφ + 1)
i
(1 − eiφ )
2
!
Visto che
− 21 (eiφ
+ 1) =
− 12 eiφ/2
−iφ/2
iφ/2
e
+e
iφ/2
= −e
eiφ/2 + e−iφ/2
φ
= −eiφ/2 cos
2
2
|
{z
}
=cos
φ
2
e
i
2
1 − eiφ = 2i eiφ/2 e−iφ/2 − eiφ/2 =
= eiφ/2
ii iφ/2
e
2i
e−iφ/2 − eiφ/2 = − 2i1 eiφ/2 e−iφ/2 − eiφ/2
φ
eiφ/2 − e−iφ/2 = eiφ/2 sin
2
|
{z
}
1
2i
=sin
φ
2
Perciò
β
α
z
}| {
}| {
φ
φ
iφ/2
iφ/2
ψx + e
ψy
= −e
cos
sin
2
2
z
ψout
• Le probabilità oggettive di osservare la particella in D1 (osservabile Y) o D2
(osservabile X) se il sistema è nello stato puro di superposizione ψout sono date
da:11
=1
z }| {
2
– Probψout {X = 1} = Probψout {Y = 0} = |α| = | − eiφ/2 |2 | cos φ2 |2 = cos2
= 21 (1 + cos φ)
– Probψout {Y = 1} = Probψout {X = 0} = |β|2 = |eiφ/2 |2 | sin φ2 |2 = sin2 φ2
= 12 (1 − cos φ)
11
Nota: | − eiφ/2 |2 = |eiφ | =
p
eiφ eiφ =
√
eiφ e−iφ =
√
1 = 1.
φ
2
4.2 L’interferometro di Mach-Zehnder
4.2.4
42
Discussione
È importante osservare che la differenziazione di cammino (fattore φ), determina se si
troveranno tutte le particelle in D1, in D2, o ogni situazione intermedia. Se per esempio
φ = 0 (cammini identici) tutte le particelle sono rilevate nel detettore D2 e nessuna in
D1. Il risultato è invertito se φ = π ed è di nuovo identico al primo quando φ = 2π,
quindi φ modifica il risultato di tutte le particelle.
In termini quantistici si dice che la particella si delocalizza nei due cammini A e B:
potenzialmente è come se essa esplorasse entrambi i cammini, se non fosse cosı̀ sarebbe
impossibile influenzare tutte le particelle modificando solo un cammino. Ciò non significa
che la particella si divide in due.
Questi effetti strani sono la manifestazione sperimentale degli stati di superposizione
e sono chiamati interferenze (quantistiche) ad una particella. La particella
interferisce con sé stessa, perché nell’interferometro passa una sola particella alla
volta. Le interferenze ad una particella appaiono quando il principio di indiscernibilità
è soddisfatto (v.cap 3.10).
Per capire meglio il concetto degli stati di superposizione, possiamo fare un semplice
paragone. Supponiamo di avere una scatola chiusa contenente una scarpa, di cui non ne
conosciamo il verso. Sappiamo allora che al suo interno c’è o la scarpa destra o quella
sinistra, ossia la scarpa è potenzialmente destra e sinistra (possiamo paragonarlo a uno
stato di superposizione). Quindi fintanto che non apriamo la scatola non possiamo
affermare con certezza quale verso ha. Quando la apriremo osserveremo però la scarpa
sinistra oppure quella destra. È dunque l’atto di osservare (processo di misura) che
ci permette di stabilire il verso della scarpa.
Se volessimo sapere in quale cammino passa la particella ?
Vediamo cosa succede se introduciamo un detettore dopo il BS1 nel cammino B
lungo la direzione di propagazione ~x per sapere dove passa la particella, ciò corrisponde
ad eseguire una misura. Il processo di misura di questo detettore genera una modifica
non deterministica dello stato del sistema e su un grande numero di particelle avremo
una conoscenza di tipo statistico, ossia uno stato misto.
Si sa che dopo la misura lo stato ψ del sistema sarà:
• ψ = ψx
se il detettore ha rilevato la particella
• ψ = ψy
se il detettore non ha rilevato la particella
L’informazione che possediamo dopo la misura sul cammino, nel caso in cui si ha un BS
equilibrato, è quindi che lo stato è ψx con probabilità (in senso statistico) 12 oppure è ψy
4.2 L’interferometro di Mach-Zehnder
43
con probabilità 12 . La matrice densità che rappresenta lo stato misto dopo il BS1 è
=ρ̂1
=ρ̂2
1 z}|{ 1 z}|{ 1
ρ̂in = Pψx + Pψy =
2
2
2
1 0
0 0
!
1
+
2
0 0
0 1
!
=
1
2
0
0
1
2
!
1
=
2
1 0
0 1
!
=
1
I
2
L’evoluzione di questo stato misto nel resto dell’interferometro è data, come per uno stato puro, dalla matrice unitaria U vista precedentemente, ma con un piccolo accorgimento:
ρ̂out = U ρ̂in U ∗ . Si ha quindi
=1
ρ̂out
1
1
1 z}|{ 1
= U I U ∗ = U I U ∗ = I U U ∗ = I = ρ̂in
2
2
2
2
Lo stato misto finale è dunque
1
I
2
Le probabilità di osservare la particella nel detettore D2 e D1, con il sistema nello stato
misto ρ̂out sono
!
1
0
2
• Probρ̂out {D2 = 1} = T r(ρ̂out Pψx ) = T r
= 21
6= Probψout {D2 = 1}
0 0
!
0 0
• Probρ̂out {D1 = 1} = T r(ρ̂out Pψy ) = T r
= 12
6= Probψout {D1 = 1}
0 21
ρ̂out =
Queste probabilità sono indipendenti dall’allungamento del cammino e sono ben diverse
da quelle calcolate precedentemente con il sistema nello stato puro ψout .
Quindi se si vuole sapere la traiettoria della particella, mettendo un detettore lungo il cammino, si perdono gli effetti di interferenza. Infatti anche il
principio di indiscerniblità viene in questo caso violato. In altre parole la conoscenza del
cammino e dell’uscita (detettore D1 o D2) sono due informazioni complementari ,
che non possono essere conosciute contemporaneamente.
Da notare infine che in questo sistema le osservabili X e Y sono compatibili, infatti
X Y =Y X
4.2.5
Conclusioni
• Una modifica su un solo cammino della particella influisce anche sull’altro, “grazie”
agli stati di superposizione.
• Le interferenze appaiono solo quando una particella può percorrere più cammini
per giungere ad uno stesso detettore e questi percorsi sono indiscernibili dopo la
detezione (principio d’indiscernibilità).
4.2 L’interferometro di Mach-Zehnder
44
• Se si vuole conoscere la traiettoria della particella, mettendo un detettore lungo il
cammino, si perdono gli effetti di interferenza (complementarità).
• In riferimento al quesito del capitolo 2.2, possiamo quindi affermare che ogni biglia
(particella) “esplora” entrambe le due possibili traiettorie per giungere al contenitore
(detettore).
4.3 L’esperienza di Rauch
4.3
4.3.1
45
L’esperienza di Rauch
Descrizione
Questa è una delle prime esperienze di interferenza quantistica ad una particella ed è stata
realizzata nel 1974 dal gruppo del professor Rauch a Vienna.
Essa è simile all’interferometro di Mach-Zehnder, visto precedentemente: ci sono due
detettori D1 e D2 dopo due cammini indiscernibili dopo la detezione della particella,
una sorgente (S) che emette neutroni, sempre uno alla volta, e tre separatori di fascio
verticali (BS).
Anche in questo sistema si modifica uno dei due cammini, mettendo in evidenza gli effetti
di interferenza ad una particella, più precisamente la delocalizzazione.
La differenziazione di uno dei cammini è data da un campo magnetico omogeneo B
che agisce sullo spin della particella (v.capp. 4.1.6 e 4.1.7), che in questa esperienza è un
neutrone. Nella figura 4.9 è schematizzato il montaggio che studieremo.
Figura 4.9: Schema dell’esperienza di Rauch.
La novità sta nel fatto che si prendono in considerazione due osservabili del
sistema contemporaneamente: la propagazione e lo spin. Matematicamente
ciò si traduce nel prodotto tensoriale fra gli stati dei due osservabili, quindi gli stati del sistema saranno dei vettori dello spazio di Hilbert H = C2 ⊗C2 .
Cosa si osserva
Il neutrone viene emesso dalla sorgente, che emana sempre una sola particella alla
volta, e incontra il primo separatore di fascio (BS1). A questo punto può venire deviato
verso l’alto o verso il basso. In seguito la particella giunge al secondo separatore (BS2)
ed è deviato verso l’alto o verso il basso. Dopo il BS2 se la particella viene deviata nei
cammini A o D viene persa. Se si trova invece a percorrere il cammino C, passa attra-
4.3 L’esperienza di Rauch
46
~ che ne modifica lo spin. Dopodichè la particella
verso un campo magnetico omogeneo B
incontra il terzo beam splitter (BS3) che la devia verso il detettore D1 (propagazione
~y ) oppure verso il detettore D2 (propagazione ~x). Si constata che facendo variare
~ si riesce a modificare il risultato della
il campo magnetico omogeneo B
detezione di tutti i neutroni , analogamente all’esperienza precedente (interferometro
di Mach-Zehnder) in cui la variazione della differenziazione φ incideva sulle detezioni.
Immagini [5]
Figura 4.10: Schema dei tre separatori di fascio verticali e del campo magnetico omogeneo.
Figura 4.11: A sinistra: foto del montaggio originale dell’esperienza di Rauch. A destra:
foto dei tre separatori di fascio verticali, schematizzati nella figura 4.10.
4.3 L’esperienza di Rauch
4.3.2
47
Modellizzazione
In questa formalizzazione sfrutteremo alcuni risultati acquisiti nello studio del sistema
spin 12 (v.capp. 4.1.2 e 4.1.3) e nell’interferometro di Mach-Zehnder (v.capp. 4.2.2 e
4.2.3).
I risultati possibili della misura con i detettori sono due: la particella è rilevata, a cui
associamo per semplicità il valore 1, oppure no, a cui associamo il valore 0.
La particella è caratterizzata, diversamente dalle due esperienze precedenti, con due osservabili: la propagazione e lo spin.
Lo stato puro dell’osservabile propagazione è dato da un vettore ψpropagazione ∈ H1 = C2
e quello dello spin da un vettore ψspin ∈ H2 = C2 . Per descrivere queste due proprietà si
usa un nuovo spazio di Hilbert, notato12 H1 ⊗ H2 = C2 ⊗ C2 , ossia il prodotto tensoriale
dello spazio H1 che descrive gli stati legati alla propagazione e dello spazio H2 che descrive
le proprietà dello spin. Questo perché uno stato puro del sistema è rappresentato da
Ψ = ψpropagazione ⊗ ψspin
che appartiene appunto allo spazio di Hilbert H = C2 ⊗ C2 .
L’evoluzione di Ψ nei vari elementi del sistema (separatori e campo magnetico
omogeneo) è conosciuta, ovvero è deterministica. Il campo magnetico provoca una
rotazione dello spin del neutrone, la cui evoluzione è data da una matrice unitaria
US .
Formalizziamo ora la situazione utilizzando le informazioni apprese nei capitoli 4.1.6 e
4.1.7. Dalla tabella 4.1 del cap. 4.1.7 (ultima colonna) si nota che se il campo magnetico
è assente, allora US = I poiché ψout = ψin . Se esso provoca una rotazione dello spin di
2π, allora US = −I (poiché ψout = −ψin ) e se lo ruota di 4π, allora si ha di nuovo US = I.
Notiamo ψx lo stato di propagazione nella direzione ~x, ψy lo stato di propagazione lungo
~y , e ψs lo stato dello spin.
Ricordo che la base di H1 è {ψx , ψy } e quella di H2 è {ψ+ , ψ− } (v.capitoli precedenti).
Lo stato iniziale del sistema è
Ψin = ψx ⊗ ψs
con ψx ∈ H1 e ψs ∈ H2
poiché il neutrone si sta propagando della direzione ~x.
L’evoluzione che riguarda la propagazione è determinata dalla matrice U = UBS ⊗ I, dove
I è l’identità poiché la parte dell’evoluzione dello spin non è influenzata da quella della
propagazione.
Dopo il primo separatore verticale (BS1) lo stato è
=U
Ψ1out
12
ψs
z}|{
z }| {
= U ψin = UBS ⊗ I(ψx ⊗ ψs ) = UBS ψx ⊗ I ψs =
√
√ !
t i r
√
√
i r
t
⊗ è il prodotto tensoriale, per alcune regole di calcolo vedi l’appendice B.
1
0
!
⊗ ψs
4.3 L’esperienza di Rauch
48
√ !
√
√
t
⊗ ψs = ( t ψx + i r ψy ) ⊗ ψs
√
i r
=
Visto che i BS sono equilibrati, ossia t = r = 12 , si ha
Ψ1out = ( √12 ψx +
√i
2
√1 (ψx
2
ψy ) ⊗ ψs =
+ iψy ) ⊗ ψs
Dopo il secondo separatore verticale (BS2) lo stato è13
√
Ψ2out = U Ψ1out = UBS ⊗ I
√
√
r
√ t + ii √
2
√
√2
i √2r + i √2t
=
√1 (ψx
2
+ iψy ) ⊗ ψs =
√
√
√1 ( t + ii r)
2
√
√
√i ( r +
t)
2
!
∗
⊗ψs =
√ !
t i r
√
√
t
i r
!
⊗ψs =
h
√1
2
√1
2
√1
2
√i
2
+ ii √12 ψx +
!
√i
2
⊗ Iψs
√1
2
√1
2
=
h
√1 ψx
2
+ ii √12 ψx +
√i ψy
2
+
√i ψy
2
i
⊗ ψs =
√1
2
+
√1
2
1
√ (ψx + iψy ) + √i (ψy + iψx ) ⊗ ψs
| 2 {z
} | 2 {z
}
D [ψx ] e C [ψy ]
A [ψy ] e B [ψx ]
dove D [ψx ] e C [ψy ], ecc. sono le traiettorie della particella associati ai rispettivi stati.
Dopo il secondo beam splitter i cammini A e D sono “persi”, quindi si eliminano gli stati
associati a questi due cammini, ossia
h
i
ψx + iψy ) + √i2 (=
ψy + iψx ) ⊗ ψs
Ψ3 = √12 √12 (=
rimane perciò
√1
2
h
√1 iψy
2
i
+ ii √12 ψx ⊗ ψs = 12 (iψy − ψx ) ⊗ ψs
Poiché ora ||Ψ3 || = √12 6= ||Ψin || = 1 bisogna normalizzare Ψ3 , quindi si deve trovare
k ∈ C∗ soddisfacente a14
√
scelta
|k|
||kΨ3 || = 1 ⇐⇒ |k|||Ψ3 || = 1 ⇐⇒ √
=
1
=⇒
k
=
2
2
Perciò
Ψ3out =
√
2Ψ3 =
√1 (iψy
2
− ψx ) ⊗ ψs
Distribuendo in Ψ3out si ottiene
Ψ3out =
√1 [iψy ⊗
2 | {z
ψs − ψx ⊗ ψs ]
} | {z }
cammino C
cammino B
~ dà l’evoluzione15 U = I ⊗ US (poiché la parte della
Il campo magnetico omogeneo B
propagazione non è influenzata dall’evoluzione dello spin)
Ψ4out = U Ψ3
13
L’asterisco (*) citato fra breve significa: non semplifichiamo ii ecc, perché dopo dovremo eliminare i
cammini A e D.
14
Ricordiamo che lo stato kΨ3 equivale allo stato Ψ3 poiché i due vettori sono linearmente dipendenti.
15
V.cap. 4.1.7 pagina 31.
i
ψy ⊗ψs
4.3 L’esperienza di Rauch
49
~ è presente solo sul cammino C, quindi U agisce solo sullo stato ψs associato
Si sa che B
alla propagazione in ~y , ossia allo stato ψy :
Ψ4out =
√1
2
[I ⊗ U (iψy ⊗ ψs ) − ψx ⊗ ψs ] =
=
√1 (iψy
2
√1 (I
2
iψy ⊗ U ψs − ψx ⊗ ψs )
⊗ U ψs − ψx ⊗ ψs )
Infine dopo il terzo separatore verticale (BS3) lo stato finale è (con l’evoluzione U =
UBS ⊗ I)
Ψout = U Ψ4out = UBS ⊗ I √12 iψy ⊗ U ψs − √12 ψx ⊗ ψs
1
i
√
√
ψ ⊗ U ψs − UBS ⊗ I
ψ ⊗ ψs = UBS √i2 ψy ⊗ IU ψs − UBS √12 ψx ⊗ Iψs
= UBS ⊗ I
2 y
2 x
!
!
!
!
√
√
√
√ !
√ !
ii √
√
√t
√1
r
0
t i r
t i r
2√
2
2
√
√
⊗ψs =
⊗U ψs −
⊗U ψs −
⊗ψs
√
√
i
i
i √
√
√
√
i r
t
i
r
t
t
r
0
2
2
2
Visto che i beam splitter sono equilibrati, t = r = 21 , allora
ii √1
i √1
1 √1
i √1
√
√
√
√
Ψout =
ψ + 2 2 ψy ⊗ U ψs −
ψ − 2 2 ψy ⊗ ψs
2 2 x
2 2 x
= ii2 ψx + 2i ψy ⊗ U ψs − 21 ψx + 2i ψy ⊗ ψs = 2i ψy − 12 ψx ⊗ U ψs − 21 ψx + 2i ψy ⊗ ψs
= 2i ψy ⊗ U ψs − 21 ψx ⊗ U ψs − 12 ψx ⊗ ψs − 2i ψy ⊗ ψs
Infine rifattorizzando si ottiene
Ψout = 2i ψy ⊗ (U ψs − ψs ) − 21 ψx ⊗ (U ψs + ψs )
4.3.3
Riepilogo
Le probabilità (oggettive) di osservare un certo autovalore delle osservabili della propagazione sono date da16 :
Nota: Ψout1 = 2i ψy ⊗ (U ψs − ψs ) e Ψout2 = − 12 ψx ⊗ (U ψs + ψs )
• La probabilità di osservare il valore 1 di Y (neutrone rilevato in D1, ossia nello stato
ψy ) con il sistema nello stato Ψout è data da
ProbΨout {D1 = 1} = || Pψy ⊗ I Ψout ||2 = || Pψy ⊗ I (Ψout1 + Ψout2 ) ||2
= || Pψy ⊗ I Ψout1 + Pψy ⊗ I Ψout2 ||2
= || Pψy ⊗ I 2i ψy ⊗ (U ψs − ψs ) + Pψy ⊗ I − 12 ψx ⊗ (U ψs + ψs ) ||2
= || 2i Pψy ψy ⊗I(U ψs − ψs ) + − 12 Pψy ψx ⊗I(U ψs + ψs ) ||2 = || 2i ψy ⊗ (U ψs − ψs )||2
| {z }
| {z }
=0
=ψy
|
{z
}
=0
=
| 2i |2 ||ψy ⊗(U ψs −ψs )||2
2
= ||ψy || ||U ψs −ψs ||2 = 14 ||−(ψs −U ψs )||2 = 41 ||ψs −U ψs ||2
| {z }
1
4
=1
16
Il proiettore diventa della forma Pψ ⊗ I poiché Ψout ∈ C2 ⊗ C2 e le probabilità che ci interessano
concernono solo la propagazione (parte a sinistra di ⊗), perciò nella parte dello spin (ossia a destra di ⊗)
mettiamo l’indenità (I).
4.3 L’esperienza di Rauch
50
• La probabilità di osservare il valore 1 di X (neutrone rilevato in D2, ossia nello stato
ψx ) con il sistema nello stato Ψout è data da
ProbΨout {D2 = 1} = || (Pψx ⊗ I) Ψout ||2
= || (Pψx ⊗ I) 2i ψy ⊗ (U ψs − ψs ) + (Pψx ⊗ I) − 12 ψx ⊗ (U ψs + ψs ) ||2
= || ( 2i Pψx ψy ) ⊗ I(U ψs − ψs ) + − 12 Pψx ψx ⊗I(U ψs +ψs )||2 = ||− 21 ψx ⊗(U ψs +ψs )||2
| {z }
| {z }
=0
=ψx
{z
}
|
=0
=|−
1 2
|
2
||ψx ⊗ (U ψs + ψs )||2 = 14 ||ψx ||2 ||U ψs + ψs ||2 = 41 ||U ψs + ψs ||2
| {z }
=1
4.3.4
Discussione
Dapprima si nota che anche in questo sistema il principio di indiscernibilità è soddisfatto, d’altronde se non fosse cosı̀ non vi sarebbero gli effetti di interferenza osservati.
Da notare che le probabilità di osservare il neutrone in D1 o D2 non dipendono dallo stato
iniziale dello spin (ψs ). Infatti il fattore che influenza le probabilità è la matrice U . Essa
descrive la modifica introdotta sul cammino C, che grazie al campo magnetico omogeneo
B permette di influenzare il risultato della detezione di tutte le particelle del sistema.
Analizziamo qualche situazione interessante che mette in evidenza gli effetti di interferenza
quantistica:
~ = 0), abbiamo visto17 che U = I,
• Se il campo magnetico omogeneo è assente (ossia B
quindi
ProbΨout {D1 = 1} = 14 ||ψs − ψs ||2 = 0 e ProbΨout {D2 = 1} = 14 ||ψs + ψs ||2 = 1
• Se il campo magnetico omogeneo provoca una rotazione di 2π, abbiamo visto che
U = −I, quindi
ProbΨout {D1 = 1} = 41 ||ψs + ψs ||2 = 1 e ProbΨout {D2 = 1} = 14 || − ψs + ψs ||2 = 0
• Se il campo magnetico omogeneo provoca una rotazione di 4π, abbiamo visto che
U = I, quindi
ProbΨout {D1 = 1} = 14 ||ψs − ψs ||2 = 0 e ProbΨout {D2 = 1} = 14 ||ψs + ψs ||2 = 1
Come esposto nel capitolo 4.1, lo spin, inizialmente nello stato ψ, con una rotazione
di 2π è nello stato −ψ che rappresenta lo stesso stato di ψ (poichè i due vettori sono
collineari). Con una rotazione di 4π si ha di nuovo lo spin nello stato ψ.
Questa esperienza dimostra che il “cambio di segno” dello stato ψ ha
delle conseguenze rilevanti: grazie a questo piccolo dettaglio e agli stati di
superposizione, intervenendo su un solo cammino si riesce a capovolgere i
risultati dell’esperienza.
17
Vedi capitolo 4.1.7 pagina 31.
4.3 L’esperienza di Rauch
4.3.5
51
Conclusioni
• Quando si prendono in considerazioni due osservabili contemporaneamente (per
esempio propagazione e spin) di un sistema, si usa il prodotto tensoriale.
• La differenziazione è qui data da un campo magnetico omogeneo posto su un solo
cammino, in cui l’evoluzione temporale è deterministica, ossia conosciuta.
• Nell’esperienza si osservano effetti d’interferenza ad una particella perché il
sistema soddisfa il principio dindiscernibilità.
4.4 L’interferometro di Franson modificato
4.4
52
L’interferometro di Franson modificato
Passiamo ora a un’esperienza in cui la sorgente emette più di una particella alla
volta. Dal punto di vista matematico si tratta di una “generalizzazione” dei fenomeni
di interferenza ad una particella presentati precedentemente. Come vedremo ci saranno
anche nuove importanti conseguenze.
4.4.1
Descrizione
L’esperienza è formata da un montaggio simmetrico a destra e a sinistra della sorgente. Le due parti sono molto simili a due interferometri di Mach-Zehnder, in cui ci sono
due osservabili riferiti alla propagazione (in ~x e in ~y ), quindi complessivamente
quattro detettori che misurano le propagazioni. Al centro c’è una sorgente che emette
due particelle alla volta: una verso la sua sinistra e una verso la sua destra. Essa ha
la capacità di emanare le due particelle sempre in direzioni di propagazione opposte una
rispetto all’altra, ovvero una verso il cammino B e l’altra verso il cammino C oppure una
verso A e l’altra verso D. Non si sa però in quale direzione è effettivamente emessa la
coppia in ogni singola esperienza.
Nell’interferometro si trovano pure quattro specchi (SP nella figura 4.12), due separatori di fascio (BS) e quattro detettori (X1 , Y1 e X2 , Y2 ).
Come nell’interferometro di Mach-Zehnder inseriamo due differenziazioni dei cammini,
indichiamo con α la prima e con β la seconda.
Figura 4.12: Esperienza con l’interferometro di Franson.
Cosa si osserva
Questo sistema è molto simile a quello presentato nel capitolo 2.3. La sorgente
emette sempre una coppia di particelle alla volta, ed è regolata in modo che la coppia
di particelle successiva non venga emessa prima che le particelle della coppia precedente
siano giunte ai rispettivi detettori. Alla fine dell’esperienza, guardando solo la parte
sinistra del montaggio, si nota che il 50% delle particelle sono state rilevate in X1 e il
4.4 L’interferometro di Franson modificato
53
50% in Y1 , analogamente per la parte destra del montaggio. Se si confrontano però i
risultati di ogni coppia di particelle, si constata che se la particella sinistra della coppia
è giunta al detettore X1 allora anche l’altra è arrivata sempre in X2 , e analogamente
se è giunta al detettore Y1 si osserva che pure l’altra è arrivata sempre in Y2 . Si nota
quindi che le particelle di ogni coppia si comportano allo stesso modo, poichè entrambe
giungono sempre allo stesso detettore.
4.4.2
Modellizzazione
Consideriamo il sistema formato dalle due particelle, ossia vediamole come un’unica
entità18 . Ci troviamo perciò di fronte a un sistema composto.
Gli stati (puri) del sistema sono quindi associati a vettori dello spazio di Hilbert H =
C2 ⊗ C2 , ossia il prodotto tensoriale dello spazio H1 = C2 che descrive gli stati legati
alla direzione di propagazione della prima particella e dello spazio H2 = C2 ,
che descrive quelli legati alla direzione di propagazione della seconda particella.
Quindi ogni vettore ψa1 ⊗ ψb2 ∈ C2 ⊗ C2 rappresenta uno stato del sistema formato
dalle due particelle, come pure le possibili combinazioni lineari, ovvero gli stati di
superposizione.
Notiamo ψx1 e ψy1 gli stati di propagazione della prima particella e ψx2 e ψy2
quelli della seconda particella.
Lo stato iniziale per l’esperienza delle due particelle19 è lo stato intrecciato
Ψin =
√1 (ψ 1
x
2
⊗ ψx2 + ψy1 ⊗ ψy2 )
Osserviamo che le due particelle devono interagire alla sorgente per poter essere
in uno stato intrecciato, ovvero devono avere un passato in comune, poiché due
particelle qualsiasi non sono intrecciate.
In relazione a quanto detto nella descrizione, si vede che da Ψin non si può sapere in
quale direzione è emessa la coppia di particelle. Si sa solamente che sono emesse sempre
nella stessa direzione, infatti ψx1 ⊗ ψx2 rappresenta lo stato del sistema in cui le particelle
si propagano nella direzione ~x e ψy1 ⊗ ψy2 l’altro caso. All’inizio di questo capitolo ho
detto che questa esperienza generalizza i sistemi a una particella, perché se poniamo
ϕ = ψx1 ⊗ ψx2 e χ = ψy1 ⊗ ψy2 si ha Ψin = √12 ϕ + √12 χ che è uno stato di superposizione, già
conosciuto nei capitoli precedenti.
Torniamo ora alla formalizzazione dell’esperienza. L’evoluzione dello stato Ψin
nell’interferometro è dato dalla somma delle singole evoluzioni dei due stati
ϕ e χ, ossia ψx1 ⊗ ψx2 e ψy1 ⊗ ψy2 . I calcoli sono molto simili a quelli usati nell’interferometro
di Mach-Zehnder (v.cap. 4.2) e nell’esperienza di Rauch (v.cap. 4.3).
18
Più avanti, nel sottocapitolo della discussione, si vedrà che non ha senso considerare le due particelle
come due entità separate.
19
È importante sottolineare che gli stati intrecciati prevedono che si consideri la coppia di particelle
(unica entità), non si avrebbe alcun risultato interessante se ci si limitasse ad una sola particella.
4.4 L’interferometro di Franson modificato
54
Visto che si considera la coppia di particelle contemporaneamente, anche
l’evoluzione si riferisce ad entrambe. Matematicamente ciò si traduce nel
prodotto tensoriale fra le matrici unitarie U che danno l’evoluzione della prima particella con quelle che danno l’evoluzione della seconda particella.
Consideriamo la parte ϕ dello stato iniziale, ossia ψx1 ⊗ ψx2 , gli operatori unitari
dell’evoluzione da applicare sono in ordine20 :
• Differenziazione dei cammini21 : U (α) ⊗ U (β)
Quindi U (α) agisce sulla prima particella e U (β) sulla seconda.
• Specchio: UBS (0) ⊗ UBS (0)
• Beam splitter (equilibrati, ossia t = r = 12 ): UBS ( 21 ) ⊗ UBS ( 12 )
Applicando in ordine queste tre matrici otteniamo l’evoluzione
Uϕ = UBS ( 12 ) ⊗ UBS ( 21 ) [UBS (0) ⊗ UBS (0)] [U (α) ⊗ U (β)]
Quindi
ϕout = Uϕ ϕ = − 21 ei(α+β)
ψy1 ⊗ ψy2 − ψx1 ⊗ ψx2 + iψx1 ⊗ ψy2 + iψy1 ⊗ ψx2
Per la parte χ dello stato iniziale, ossia ψy1 ⊗ ψy2 , si ha l’evoluzione:
• Specchio: UBS (0) ⊗ UBS (0)
• Beam splitter (equilibrati, ossia t = r = 12 ): UBS ( 21 ) ⊗ UBS ( 12 )
Applicando in ordine queste due matrici otteniamo l’evoluzione
Uχ = [UBS (0) ⊗ UBS (0)] UBS ( 12 ) ⊗ UBS ( 12 )
Quindi
χout = Uχ χ = − 21
ψx1 ⊗ ψx2 − ψy1 ⊗ ψy2 + iψx1 ⊗ ψy2 + iψy1 ⊗ ψx2
Lo stato intrecciato finale è quindi dato dalla somma delle evoluzioni ottenute22 :
α+β
Ψout
20
iei 2
= √
2
α+β 1
α+β 1
1
2
1
2
2
2
sin
(ψx ⊗ ψx − ψy ⊗ ψy ) + cos
(ψx ⊗ ψy + ψy ⊗ ψx )
2
2
Gli operatori a sinistra del prodotto tensoriale agiscono sullo spazio H1 , quindi sugli stati della prima
particella, invece quelli a destra agiscono sullo spazio H2 , ossia sugli stati della seconda particella.
21
Le matrici U usate in questa modellizzazione sono quelle costruite nel capitolo dell’interferometro di
Mach-Zehnder (v.cap. 4.2).
22
Poiché l’operatore d’evoluzione U è lineare, ossia U (ϕ + χ) = Uϕ ϕ + Uχ χ.
4.4 L’interferometro di Franson modificato
4.4.3
55
Riepilogo
α+β
Poniamo γ =
iei√ 2
2
sin α+β
eξ=
2
α+β
iei√ 2
2
cos α+β
. Si ha quindi
2
Ψout = γ(ψx1 ⊗ ψx2 ) − γ(ψy1 ⊗ ψy2 ) + ξ(ψx1 ⊗ ψy2 ) + ξ(ψy1 ⊗ ψx2 )
| {z }
| {z }
| {z }
| {z }
=ϕ
=χ
=ω
=ϑ
Le probabilità di osservare la coppia nei rispettivi detettori X1 , Y1 della prima
particella e X2 , Y2 della seconda particella sono date da:
α+β
1
1
= [1−cos(α+β)]
ProbΨout {X1 = 1; X2 = 1} = ||(Pψx1 ⊗Pψx2 )Ψout ||2 = ||γϕ||2 = |γ|2 = sin2
2
2
4
1
α+β
1
ProbΨout {Y1 = 1; Y2 = 1} = ||(Pψy1 ⊗Pψy2 )Ψout ||2 = ||γχ||2 = |γ|2 = sin2
= [1−cos(α+β)]
2
2
4
1
α+β
1
ProbΨout {X1 = 1; Y2 = 1} = ||(Pψx1 ⊗Pψy2 )Ψout ||2 = ||ξω||2 = |ξ|2 = cos2
= [1+cos(α+β)]
2
2
4
α+β
1
1
= [1+cos(α+β)]
ProbΨout {Y1 = 1; X2 = 1} = ||(Pψy1 ⊗Pψx2 )Ψout ||2 = ||ξϑ||2 = |ξ|2 = cos2
2
2
4
4.4.4
Discussione
Il principio di indiscernibilità, che anche in questo esperimento è soddisfatto, enuncia che
abbiamo delle interferenze.
Dalle probabilità oggettive si nota subito qualcosa di strano: i fattori α e β, che sono presenti uno sull’interferometro di sinistra e uno su quello di destra, influenzano entrambi
il risultato della misura di ogni particella. Se si variasse il fattore α si dovrebbe
modificare, secondo l’intuito, solo il risultato della prima particella (detettori
X1 e Y1 ). Invece non è cosı̀: la modifica di un solo cammino di una particella
influisce sul risultato globale dell’esperienza. Questi effetti sono la manifestazione sperimentale degli stati intrecciati e sono chiamati interferenze a due particelle.
Cosa succederebbe se si guardasse ogni particella singolarmente?
Vediamo ora cosa succederebbe se considerassimo ogni particella della coppia l’una
indipendente dall’altra. Avremmo le probabilità seguenti (per la particella 1):
• Prob{X1 = 1} = Prob{X1 = 1; X2 = 1} + Prob{X1 = 1; Y2 = 1} = 12 (sin2 α+β
+
2
1
2 α+β
cos 2 ) = 2 poiché il risultato della particella 2 non ci interessa, quindi è
indifferente se X2 = 1 o Y2 = 1.
• Prob{Y1 = 1} = Prob{Y 1 = 1; X2 = 1} + Prob{Y1 = 1; Y2 = 1} = 21 (cos2 α+β
+
2
α+β
sin2 2 ) = 12
Come si vede queste probabilità sono completamente diverse da quelle trovate precedentemente. Inoltre adesso sono indipendenti dai fattori α e β, quindi non c’è
4.4 L’interferometro di Franson modificato
56
più alcun effetto di interferenza.
Ritorniamo ora al primo caso, dove consideriamo la coppia, e cerchiamo di caratterizzare meglio queste interferenze.
Dalle probabilità si nota che scegliendo opportunamente i parametri α e β (per esempio
α = β = 0) si può ottenere che tutte le particelle siano rilevate (con probabilità 1) sempre
una nello stesso detettore dell’altra23 , ossia X1 = 1 e Y2 = 1 oppure Y1 = 1 e X2 = 1. Ciò
accade per ogni coppia di particelle e si parla quindi di correlazione perfetta, ovvero
per qualsiasi misura la coppia dà sempre lo stesso risultato.
Si è quindi introdotto un nuovo effetto puramente quantistico24 : le correlazioni
quantistiche.
Nei casi di correlazione perfetta quando si conosce il risultato di una particella, allora
si conosce con certezza anche il risultato dell’altra. Se, per esempio, la prima particella
giunge al detettore X1 , allora si è sicuri che la seconda particella è stata rilevata in
Y2 , e viceversa. Questa conseguenza delle correlazioni sarà di fondamentale
importanza quando affronteremo il capitolo dedicato al teletrasporto.
Inversamente, nei casi di anticorrelazione perfetta, si avrà sempre un risultato
opposto delle detezioni: per esempio, una particella in X1 e l’altra in X2 .
Per capire meglio il concetto, possiamo paragonare la coppia di particelle ad un paio
di scarpe, più precisamente la particella 1 alla scarpa sinistra e la 2 alla scarpa destra.
Ora mettiamo la scarpa sinistra in una scatola e in un’altra scatola uguale alla prima ci
mettiamo la scarpa destra. Poi “mescoliamo” le scatole senza guardare. A questo punto
non siamo più in grado di stabilire con certezza in quale scatola si trova una certa scarpa
(possiamo paragonare questa situazione allo stato intrecciato), ma sappiamo solo che
se apriamo una scatola troviamo con probabilità 12 quella sinistra e con probabilità 12
quella destra. Apriamo dunque una delle due scatole (possiamo paragonare al processo di
misura): se troviamo la scarpa destra siamo sicuri che nell’altra scatola ci sarà la scarpa
sinistra, senza doverla aprire (ossia senza compiere una misura) e indipendentemente
dalla distanza fra le due scatole.
L’affermazione, detta all’inizio di questo capitolo, che due particelle
correlate devono essere considerate come un’unica entità trova quindi senso, poichè, grazie alle interferenze, intervenendo unicamente sul cammino
di un solo interferometro di una sola particella si riesce a influenzare anche
l’altra particella modificandone il risultato, passando per esempio da una
situazione di correlazione perfetta a una di anticorrelazione. Perciò siamo
obbligati a concludere che le due particelle non si possono considerare come
due entità separate indipendenti fra loro.
23
24
Per stessi detettori si intende: X1 ; Y2 (verso il basso) oppure Y1 ; X2 (verso l’alto).
In seguito, nella discussione, vedremo che una spiegazione classica delle correlazioni è impossibile.
4.4 L’interferometro di Franson modificato
57
Come fanno due particelle separate fisicamente ad avere un comportamento cosı̀ simile, ossia ad essere correlate ?
Abbiamo visto che le correlazioni appaiono quando una coppia di particelle è in
uno stato intrecciato. Analizziamo 4 possibili tesi (che verificheremo) che potrebbero
spiegare per quale motivo le due particelle sono correlate.
Le correlazioni potrebbero essere spiegate grazie a 4 tesi:
Teorie di tipo classico:
1. Avviene uno scambio di informazioni fra le due particelle (teoria senza variabili
nascoste 25 ).
2. Le correlazioni sono già stabilite alla sorgente (teoria locale con variabili nascoste
locali ).
Altre teorie, di tipo non locale:
3. Le correlazioni sono stabilite al momento della misura (teoria con variabili nascoste
non locali ).
4. Le due particelle vanno considerate come un’unica entità, come vuole la fisica
quantistica (teoria senza variabili nascoste).
Le teorie locali sono quelle che sostengono che le due particelle della coppia sono indipendenti fra loro, ossia il risultato di una qualsiasi misura effettuata sulla prima
particella non dipende da una qualsiasi altra misura effettuata sulla seconda e viceversa.
Le teorie non locali sono quelle che invece sostengono che due sistemi (le due particelle
della coppia) anche se sono spazialmente molto separati, si influenzano vicendevolmente
e non possono quindi essere considerati come due entità separate.
L’ipotesi della località è quella che si predilige in una visione classica della
fisica, perciò escludere ogni possibile teoria locale equivale ad escludere ogni
teoria classica.
Esaminiamo ora le due possibili teorie classiche.
1. Avviene uno scambio di informazioni fra le due particelle ?
Se ha luogo uno scambio di informazioni fra le due particelle, significa che la prima
particella che viene rilevata invia un’indicazione all’altra sul suo risultato e quindi
quest’ultima reagisce andando allo stesso detettore della prima nel caso della correlazione
e in quello opposto nel caso dell’anticorrelazione.
Si constata però che le correlazioni si manifestano anche se le particelle sono separate
25
Fra breve vedremo cosa sono le variabili nascoste.
4.4 L’interferometro di Franson modificato
58
da una grande distanza26 , perciò se avvenisse uno scambio di informazioni il segnale
per giungere in tempo affinchè possa “avvisare” l’altra particella27 , dovrebbe avere una
velocità superiore a quella della luce. Come sappiamo dalla teoria della relatività un
segnale non può propagarsi più velocemente della luce.
Questa tesi è quindi smentita dagli esperimenti in accordo con la teoria
della relatività.
2. Le correlazioni sono già stabilite alla sorgente ?
Se le correlazioni sono stabilite già alla fonte, significa che ogni particella quando
viene emessa dalla sorgente “sa” già come dovrà reagire quando incontra un determinato
tipo di apparecchio di misura e ciò indipendentemente dalle possibili misure effettuate
sull’altra particella.
Su questa tesi ci lavorarono lo scienziato A. Einstein dapprima e J.S. Bell in seguito. Bell
nel 1964 elaborò un criterio per verificare la validità di tutte le possibili teorie
locali . Si suppone che la particella 1 può essere soggetta alle misure α e α0 che possono
dare solo due risultati: +1 (che corrisponde nella nostra esperienza a Y1 = 1) oppure −1
(che corrisponde nella nostra esperienza a X1 = 1). La particella 2 può essere sottoposta
alle misure β e β 0 che possono dare solo due risultati: +1 (che corrisponde nella nostra
esperienza a X2 = 1) oppure −1 (che corrisponde nella nostra esperienza a Y2 = 1). Se le
correlazioni sono stabilite alla sorgente, ovvero se si ha una teoria locale, allora la prima
particella deve partire dalla sorgente con una lista
λ1 = {r1 (α), r1 (α0 )}
e la seconda particella con una lista
λ2 = {r2 (β), r2 (β 0 )}
dove r1 (α) rappresenta il risultato della detezione che la particella 1 darebbe se incontrasse la differenziazione α sul cammino A, rispettivamente r2 (β) è il risultato della detezione
che la particella 2 darebbe se incontrasse la differenziazione β sul cammino B. Ricordiamo che r1 (α) e r1 (α0 ) non dipendono dalle misure effettuate sulla particella
2 , e r2 (β) e r2 (β 0 ) non dipendono a loro volta dalle misure effettuate sulla particella 1
(Principio delle cause locali ). Quindi r1 (α) può prendere solo i valori +1 (se rilevato
in Y1 ) oppure −1 (se rilevato in X1 ), analogamente per r1 (α0 ), r2 (β) e r2 (β 0 ).
La coppia λ = {λ1 , λ2 } è chiamata variabile nascosta.
Possiamo quindi spiegare le correlazioni grazie a queste liste. Se si osserva una correlazione quando l’interferometro della particella 1 ha l’allungamento α e quello della
particella 2 ha l’allungamento β significa, che, per esempio, la particella 1 della coppia è partita con la lista λ1 = {r1 (α) = 1, r1 (α0 ) = −1} e la particella 2 con la lista
26
Come verificato da un’esperienza svoltasi a Ginevra nel 1998, dove sono state osservate correlazioni
su delle distanze di 10,9 km [10].
27
Ricordo che la sorgente emette le due particelle della coppia contemporaneamente.
4.4 L’interferometro di Franson modificato
59
λ2 = {r2 (β) = 1, r2 (β 0 ) = 1}.
Bell formalizzò cosı̀ la sua affermazione, enunciando il teorema di Bell, valido solo
con l’ipotesi della località (ossia del principio delle cause locali), che può essere cosı̀ scritto: Esiste una grandezza S, calcolabile a partire dalle variabili
nascoste λ, tale che
• (i) Se le correlazioni sono stabilite alla sorgente e quindi la teoria locale è valida,
hSi è limitato in un certo intervallo [a, b].
• (ii) Se hSi esce da questo intervallo, allora le correlazioni non sono stabilite alla
sorgente. Quindi se hSi ∈
/ [a, b] la teoria non può essere locale.
Dal punto (i) si deduce la relazione a ≤ hSi ≤ b, che è chiamata disuguaglianza di
Bell . Se il valore medio di S misurato è minore di a o maggiore di b si dice che la
disuguaglianza di Bell è violata, e da (ii) si conclude che le correlazioni non
possono essere stabilite alla fonte. Per stabilire ciò non è stata fatta alcuna
supposizione di tipo quantistico.
La grandezza S nell’esperienza dell’interferometro di Franson vale28
S(λ) = [r1 (α) + r1 (α0 )]r2 (β) + [r1 (α) − r1 (α0 )]r2 (β 0 )
= r1 (α)r2 (β) + r1 (α0 )r2 (β) + r1 (α)r2 (β 0 ) − r1 (α0 )r2 (β 0 )
Cerchiamo ora entro quali limiti è compresa questa grandezza. Sapendo che ri (. . .) può
assumere solo i valori ±1, si ha quindi
−2 ≤ S(λ) ≤ 2
Perciò dal teorema di Bell ricaviamo che: Se le correlazioni sono stabilite già alla
sorgente, allora |hS(λ)i| ≤ 2.
La grandezza S(λ) tiene conto di più situazioni sperimentali diverse allo stesso tempo, per
esempio abbiamo r1 (α0 ) e r1 (α) che non danno quindi la possibilità di fare con la stessa
coppia sia l’esperienza con l’allungamento α0 sia quella con l’allungamento α contemporaneamente. Perciò, per motivi sperimentali, siamo costretti a fare diverse esperienze con
più coppie e il risultato sarà quindi conosciuto in termini di valori medi. Se −2 ≤ S(λ) ≤ 2
allora è evidente che anche con il valor medio si ha −2 ≤ hS(λ)i ≤ 2, questa relazione è
la disuguaglianza di Bell che dobbiamo verificare.
Calcoliamo ora il valore medio della grandezza S(λ), sapendo che per esempio hr1 (α)r2 (β)i
è la somma sulle combinazioni di risultati possibili ponderate con le rispettive probabilità,
ossia:
hr1 (α)r2 (β)i = 1 · 1 · Prob{r1 = +1; r2 = +1} + 1 · (−1) · Prob{r1 = +1; r2 = −1}
28
Questo valore della grandezza S non è specifico per questa esperienza, ma vale per qualsiasi montaggio
in cui si possono effettuare due misure per particella e ognuna di queste misure dà i risultati +1 o −1.
4.4 L’interferometro di Franson modificato
60
+(−1) · 1 · Prob{r1 = −1; r2 = +1} + (−1) · (−1) · Prob{r1 = −1; r2 = −1}
= Prob{r1 = r2 } − Prob{r1 6= r2 }
Questo valore medio si chiama coefficiente di correlazione ed è notato
E(α, β) = hr1 (α)r2 (β)i.
Analogamente gli altri coefficienti di correlazione, cioè
E(. . . , . . .) = Prob{risultati uguali} − Prob{risultati diversi}.
A questo punto possiamo esprimere hS(λ)i come somma dei rispettivi coefficienti di
correlazione, ossia
hS(λ)i = E(α, β) + E(α0 , β) + E(α, β 0 ) − E(α0 , β 0 )
Abbiamo ora un criterio che ci permette di verificare le teorie locali .
Predizione della meccanica quantistica:
Vediamo ora se la disuguaglianza di Bell è soddisfatta o violata dalla teoria quantistica.
Grazie alle probabilità che sono state calcolate nel capitolo 4.4.3, si può trovare il valore
di ogni singolo coefficiente di correlazione (teorico), per esempio
E(α, β) = 2 · Prob{X1 = 1; Y2 = 1} − 2 · Prob{X1 = 1; X2 = 1}
1
1
= 2 · [1 + cos(α + β)] − 2 · [1 − cos(α + β)] = cos(α + β)
4
4
Quindi
hS(λ)i = cos(α + β) + cos(α0 + β) + cos(α + β 0 ) − cos(α0 + β 0 )
Inserendo i valori α = 0, α0 = π2 , β = − π4 , β 0 =
π
4
si ottiene
√
hS(λ)i = cos(0 − π4 ) + cos( π2 − π4 ) + cos(0 + π4 ) − cos( π2 + π4 ) = 2 2
Perciò
√
|hS(λ)i| = 2 2 =⇒ |hS(λ)i| > 2
La disuguaglianza di Bell è violata secondo la teoria della meccanica
quantistica, quindi la meccanica quantistica è una teoria non locale.
Verifica sperimentale della disuguaglianza di Bell:
Non ci resta che verificare sperimentalmente se è corretta la previsione della teoria
quantistica, o se invece sono corrette le teorie locali, in base al criterio stabilito precedentemente. Se le predizioni della teoria quantistica saranno confermate, ossia se la
disuguaglianza di Bell verrà violata, allora le correlazioni non sono spiegabili con delle
teorie di tipo locale.
Io non ho potuto realizzare questa esperienza perché richiede apparecchiature sofisticate,
che sono usate solo dai centri di ricerca. Perciò mi affido ai risultati di tre esperienze
storiche, fatte nel 1981, 1982 e 1999.
4.4 L’interferometro di Franson modificato
61
La prima [7] era composta da un montaggio molto simile al nostro. La disuguaglianza di
Bell che si voleva verificare era uguale alla nostra, ossia
−2 ≤ hSi ≤ 2
La predizione della teoria quantistica per il montaggio dell’esperimento era
hSM Q i = 2.70
con un margine di errore teorico di ±0.05.
Il risultato sperimentale di questo esperimento fu
hSesperimento i = 2.697
con un margine d’errore sperimentale di ±0.015.
Questo esperimento mostra quindi una grande violazione della disuguaglianza di
Bell e i risultati sperimentali sono in perfetto accordo con la predizione della meccanica quantistica. I risultati di questo esperimento furono criticati poichè i
detettori avevano una bassa efficienza e i tipi di misure effettuate erano fissi durante tutta
l’esperienza.
Il secondo esperimento fatto nel 1982 [8], era formato da un montaggio simile a quello
precedente, ma con la novità che i tipi di misura a cui erano soggette le particelle continuavano a cambiare in modo casuale e indipendente fra l’apparecchio della prima particella e
quello della seconda. La velocità di cambiamento degli apparecchi di misura (10 ns) era
tale da impedire uno scambio di un segnale fra le particelle (v. argomento dell’ipotesi 1)
e quindi la “scelta” della misura a cui erano soggette le particelle avveniva quando esse
avevano già lasciato la sorgente.
In questo esperimento la disuguaglianza di Bell da verificare era leggermente diversa
dalla nostra, ossia
−1 ≤ hSi ≤ 0
La predizione della teoria quantistica per il montaggio dell’esperimento era
hSM Q i = 0.112
Il risultato sperimentale di questo esperimento fu
hSesperimento i = 0.101
con un margine d’errore sperimentale di ±0.020.
Anche in questo esperimento si constata che la disuguaglianza di Bell è violata e
che i risultati sperimentali sono in accordo con la predizione della meccanica
quantistica.
Il terzo esperimento fatto nel 1999 [9], era formato da un montaggio simile a quello
precedente con la differenza che gli apparecchi di misura della prima particella e quelli
4.4 L’interferometro di Franson modificato
62
della seconda sono distanti fra loro 400 m. Inoltre i detettori erano molti più accurati
rispetto a quelli usati nei precedenti esperimenti.
I risultati di questa esperienza sono in eccellente accordo con le predizioni
quantistiche, e mostrano un’indiscutibile violazione delle disuguaglianze di
Bell .
Dalla (ii) di pagina 59 concludiamo che le correlazioni non sono stabilite
alla sorgente.
Quindi nessuna teoria locale, ovvero di tipo classico, può essere utilizzata per spiegare le correlazioni osservate negli esperimenti .
Esaminiamo ora le altre due teorie, di tipo non locale.
3. Le correlazioni sono stabilite al momento della misura ?
Questa tesi è di tipo non locale (con variabili nascoste non locali ), ciò significa che il
risultato di una misura effettuata sulla particella 1 dipende dal risultato della misura
effettuata sulla particella 2, e viceversa. Sarebbe quindi una teoria con delle variabili
nascoste non locali, poiché il principio delle cause locali in questa tesi non è valido. Inoltre
essa prevede uno scambio di informazioni fra le due particelle, altrimenti non potrebbero
influenzarsi una con l’altra comunicandosi quale misura hanno subito. Come abbiamo
visto le correlazioni sono state osservate anche con grandi distanze fra i due apparecchi
di misura [10], quindi un’informazione dovrebbe propagarsi più velocemente della luce
per giugnere in tempo alla seconda particella e poter cosı̀ influenzare il risultato della
sua misura; ma la teoria della relatività impone come velocità massima di propagazione
di un’informazione quella della luce, come verificato sperimentalmente di recente [11].
Perciò pure la tesi che le correlazioni sono spiegabili con delle variabili
nascoste non locali è da escludere.
4. Le due particelle vanno considerate come un’unica entità ?
L’unica tesi che è in accordo sia con i risultati sperimentali sia con la
teoria della relatività è quella della teoria quantistica, ossia che le due
particelle devono essere considerate con un’unica entità (attraverso gli
stati intrecciati). Infatti l’indeterminazione oggettiva (probabilità) della meccanica
quantistica è tale da precludere ogni possibilità di approfittare della non località per
mandare delle informazioni più velocemente della luce.
Nel prossimo capitolo vedremo come gli stati intrecciati , e quindi la non località,
saranno determinanti per la realizzazione del teletrasporto.
4.4 L’interferometro di Franson modificato
4.4.5
63
Conclusioni
• Le correlazioni appaiono quando una coppia di particelle è in uno stato
intrecciato;
• Si parla di correlazioni quando entrambe giungono allo stesso detettore, e di anticorrelazioni se danno detezioni opposte;
• Una modifica su un solo cammino di una sola particella influisce anche sul cammino
dell’altra particella (non località);
• Le correlazioni sono un processo non locale: anche se le particelle della coppia
fossero separate da enormi distanze, le si osserverebbero sempre.
• Non è possibile dare una spiegazione classica (locale) delle correlazioni: esse sono un effetto puramente quantistico legato all’esistenza degli
stati intrecciati.
• In riferimento al quesito del capitolo 2.3, possiamo quindi affermare che le due biglie
(particelle) di ogni coppia si comportano allo stesso modo, e vanno perciò trattate
come un’unica entità.
4.5 Il Teletrasporto
4.5
4.5.1
64
Il Teletrasporto
Introduzione
Quando si parla di teletrasporto la nostra immaginazione ci spinge verso la fantascienza,
ricordando mezzi di trasporto come quelli usati dai protagonisti del film Star Trek.
Purtroppo il teletrasporto che viene ora realizzato in laboratorio è molto lontano da
questo tipo di applicazioni, ma è comunque un primo passo per la realizzazione delle reti
con cui comunicheremo in futuro.
Le prime idee di sfruttare la meccanica quantistica per realizzare il teletrasporto risalgono
all’anno 1993, ma la comunità scientifica, a quel tempo, era scettica poiché riteneva che
sarebbe stato troppo complesso realizzare tale esperimento in laboratorio. Seguirono i
primi tentativi, guidati dal professor Zeilinger dell’Università di Innsbruck, che riuscı̀ a
teletrasportare una caratteristica di un fotone, ossia una particella di luce, su un altro
fotone non collegato al primo, dall’altra parte dello stesso tavolo. Nel gennaio 2003, a
Ginevra, il Gruppo di Fisica applicata dell’Università di Ginevra guidato dal professor
Gisin, è riuscito a teletrasportare un fotone da un laboratorio a un altro distante 55 m
ma collegato al primo tramite 2 km di fibre ottiche.
Recentemente, nel mese di agosto 2004, sono stati raggiunti due importanti traguardi nel
campo del teletrasporto: due gruppi di scienziati, uno del National Institute of Standards
and Technology negli USA e l’altro all’Università di Innsbruck in Austria, sono riusciti a
teletraspostare degli atomi (gli statunitensi un atomo di berillio e gli austriaci un atomo
di calcio).
Per ora il teletrasporto di esseri viventi non è possibile, poiché dal punto di vista fisico
sono dei sistemi troppo complessi, anche se dal punto di vista teorico ciò è possibile.
Visto che un corpo è formato da circa 1023 atomi, per memorizzare su un computer i dati
necessari al teletrasporto (e quindi alla creazione di uno stato quantistico) servirebbero
1034 bits (ossia un po’ meno di 10 milioni di miliardi di miliardi di gigabyte GB). Il
problema più grande si porrebbe dunque, non tanto nella conservazione di questi dati (se
fossero registrati su dei CD-ROMs corrisponderebbe a un cubo di lato 1’000 km), bensı̀
nella loro trasmissione: le migliori linee di comunicazione odierne arrivano a trasmettere
al massimo 10 miliardi di bits al secondo e quindi occorrerebbero circa 30 milioni di
miliardi di anni (1024 secondi) per trasferire questa enorme quantità di informazioni.
In conclusione di questo capitolo vedremo quali potranno essere le future applicazioni del
teletrasporto, soprattutto nel campo dell’informatica e delle telecomunicazioni.
4.5.2
Descrizione
Vediamo cosa si intende per teletrasporto. Si tratta di “scomporre” un oggetto, nel
nostro caso un atomo (o una particella), e di “ricomporlo” in un altro luogo. In altre
4.5 Il Teletrasporto
65
parole consiste nel trasferire le proprietà di una particella a un’altra, tramite una terza
particella “mediatrice”. Attualmente la distanza tra la stazione di trasmissione e quella
di ricezione non supera il chilometro, per motivi tecnologici.
Per illustrare i principi fondamentali di questo fenomeno consideriamo un esempio
semplificato, ma di facile comprensione. Immaginiamo che Alice, sulla Terra, voglia
teletrasportare un oggetto (particella C) a Bob, che si trova su Marte. La strumentazione
minima è di due “cabine”, il cui interno sia perfettamente isolato dal mondo esterno.
Nella cabina sulla Terra, Alice inserisce l’oggetto e della “materia ausiliaria” (particella
A). Questa “materia ausiliaria” deve avere un “gemello”(particella B) su Marte, che
deve essere dotato di una proprietà per noi insolita, ma possibile nel mondo quantistico:
se si modifica la “materia ausiliaria” sulla Terra, anche la “materia ausiliaria” su Marte
si modifica istantaneamente (in termini quantistici ciò significa che le particelle A e B
sono correlate, ossia in uno stato intrecciato, v.cap. 4.4). Alice preme ora un pulsante,
che fa interagire l’oggetto (C) con la “materia ausiliaria” sulla Terra (A). Durante questo
processo Alice perde la struttura del suo oggetto, perché deve fare una misura sulle
particelle A e C, che ha appena fatto interagire (lo impongono le leggi della meccanica
quantistica) e le caratteristiche del suo oggetto vengono istantaneamente trasferite alla
materia gemella (B), su Marte. Per completare il trasferimento Alice deve ancora inviare
in maniera tradizionale (per esempio via radio) alla cabina di Bob il risultato della misura
che ha effettuato a Terra. A questo punto il trasferimento è completo e si accende una
spia: Bob può aprire la cabina e prendere l’oggetto.
Abbiamo quindi visto che in realtà quello che viene trasferito non è
la materia che forma l’oggetto, ma le sue caratteristiche sotto forma di
informazioni e quindi di stati quantistici .
Il teletrasporto combina le leggi più rilevanti della meccanica quantistica trattate nei
capitoli precedenti, in particolare le correlazioni (stati intrecciati) e il principio
di sovrapposizione degli stati (stati di superposizione).
Vediamo ora di rendere più formale il protocollo di teletrasporto.
Lo schema è descritto nella Figura 4.13.
Alice vuole teletrasportare a Bob la particella C. Per fare ciò lo stato ϕ della particella
C deve essere inviato a Bob.
Iniziamo a dare a Alice e a Bob due particelle A e B, per esempio due fotoni, che devono
essere correlate 29 e quindi trovarsi in uno stato intrecciato (nella modellizzazione
vedremo perché questa condizione è necessaria). Queste coppia di particelle rappresenta
quella che nell’esempio precedente abbiamo chiamato “materia ausiliaria”.
A questo punto Alice fa interagire la particella C che vuole teletrasportare, per esempio
29
Vedi capitolo 4.4.
4.5 Il Teletrasporto
66
Figura 4.13: Schema del protocollo di teletrasporto.
un atomo. È importante notare che Alice non deve necessariamente conoscere lo stato
(ϕ) della particella C. Per esempio se lo stato ϕ rappresenta lo spin (v.cap. 4.1) della
particella C, come una superposizione di stati30 , sappiamo (per il postulato della misura
ideale) che non è possibile misurare lo spin senza perturbare lo stato del sistema e quindi
lo spin stesso. Quindi è un vantaggio poter teletrasportare lo stato della particella senza
doverlo obbligatoriamente conoscere. Con una comunicazione classica 31 ciò non sarebbe
possibile, perché se volessimo trasmettere le informazioni relative alla particella dobbiamo
ovviamente conoscerne lo stato, e questo come visto non è fattibile senza perturbarlo.
Alice facendo interagire C con A, intreccia lo stato di A (ossia lo stato intrecciato della
coppia di particelle A, B) con lo stato di C (ϕC ).
Ora Alice compie una misura sulla coppia di particelle (A, B), chiamata misura di
Bell 32 . Come visto nel capitolo 3.7 quando si procede alla misura si osservano gli
autovalori dell’osservabile che sono a loro volta associati agli autovettori dell’osservabile,
che in questo caso sono i vettori della base di Bell. La misura che attua Alice può dare
4 possibili risultati (autovalori λ1 , λ2 , λ3 , λ4 ), che sono associati ai 4 vettori della base di
Bell {Φ+ , Φ− , Ψ+ , Ψ− } che vedremo nella modellizzazione.
La misura di Bell modifica lo stato ϕC della particella C e quindi Alice “perde” la sua
particella.
Per esempio lo stato di superposizione ϕ+ = √12 ψ+ + √12 ψ− .
Intesa come trasmissione di informazioni attraverso canali classici, per esempio fibre ottiche.
32
Poiché l’osservabile misurato ha come autovettori i vettori della base di Bell, che si vedranno nella
modellizzazione.
30
31
4.5 Il Teletrasporto
67
Alice deve ora inviare a Bob classicamente 33 il risultato della sua misura di Bell, ossia
quale autovalore λi ha osservato. Per fare ciò bastano due bits di dati classici 34 . Quando
arrivano a Bob questi due bits, lui deve apportare una correzione allo stato ψ B della
sua particella B in funzione del risultato della misura di Bell che ha appena ricevuto da
Alice. Ora la particella di Bob è nello stato ϕ, quindi la particella C è stata teletrasportata.
Nella modellizzazione non ci sarà alcuna novità a livello teorico, si tratterà solo di
applicare i concetti appresi finora dai capitoli precedenti.
4.5.3
Modellizzazione
Passiamo ora a formalizzare il protocollo di teletrasporto.
Abbiamo detto che inizialmente due particelle correlate vengono date una ad Alice
e l’altra a Bob.
Lo stato iniziale di questa coppia di particelle A e B correlate è dato dallo stato
intrecciato
A
B
A
B
√1
ΦAB
∈ HA ⊗ HB
+ = 2 ψ+ ⊗ ψ+ + ψ− ⊗ ψ−
Con il protocollo visto prima non si trasferisce materia, ma informazioni sotto forma di
stati quantistici. È quindi necessario conoscere informazioni sulla particella C, ossia il suo
stato.
Lo stato (puro) ϕ della particella C da teletrasportare è
C
C
ϕC = αψ+
+ βψ−
∈ HC
Successivamente si fa interagire la particella C con la particella A. In termini quantistici
ciò equivale a intrecciare lo stato di A e B con lo stato di C , ossia
C
C
Θ = ϕC ⊗ ΦAB
+ = (αψ+ + βψ− ) ⊗
C
= αψ+
⊗
√1 (ψ A
+
2
√1 (ψ A
+
2
B
A
B
⊗ ψ+
+ ψ−
⊗ ψ−
)
B
A
B
C
⊗ ψ+
+ ψ−
⊗ ψ−
) + βψ−
⊗
√1 (ψ A
+
2
∈ H = HC ⊗ HA ⊗ HB
B
A
B
⊗ ψ+
+ ψ−
⊗ ψ−
)
C
A
B
C
A
B
C
A
B
A
B
C
+ βψ−
⊗ √12 ψ−
= αψ+
⊗ √12 ψ+
⊗ ψ+
+ αψ+
⊗ √12 ψ−
⊗ ψ−
+ βψ−
⊗ √12 ψ+
⊗ ψ+
⊗ ψ−
|
{z
} |
{z
} |
{z
} |
{z
}
α
C ⊗ψ A ⊗ψ B )
= √ (ψ+
+
+
2
=
α
√
(ψ C
2 |+
α
C ⊗ψ A ⊗ψ B )
= √ (ψ+
−
−
2
A
B
C
A
B
⊗ ψ+
⊗ψ+
+ ψ+
⊗ ψ−
⊗ψ−
)+
{z }
| {z }
(1)
(2)
β
C ⊗ψ A ⊗ψ B )
= √ (ψ−
+
+
2
β
√
(ψ C
2 |−
β
C ⊗ψ A ⊗ψ B )
= √ (ψ−
−
−
2
A
B
C
A
B
⊗ ψ+
⊗ψ+
+ ψ−
⊗ ψ−
⊗ψ−
)
{z }
| {z }
(3)
(4)
I vettori (1), (2), (3), (4) formano una base canonica (ortonormata) B1 di HC ⊗ HA .
A questo punto Alice sta per compiere la misura di Bell sulle particelle C e A, ossia
la misura di un’osservabile S i cui autovalori {λi }4i=1 sono associati agli autovettori della
33
34
Via radio o tramite fibre ottiche.
Vedremo in dettaglio nella modellizzazione cosa rappresentano i due bits.
4.5 Il Teletrasporto
68
CA
CA
CA
base di Bell (ortonormata) B2 = {ΦCA
+ , Φ− , Ψ+ , Ψ− } dello spazio di Hilbert HC ⊗ HA ,
con
ΦCA
+ =
√1 (ψ C
+
2
A
C
A
⊗ ψ+
+ ψ−
⊗ ψ−
)
ΦCA
− =
√1 (ψ C
+
2
A
C
A
⊗ ψ+
− ψ−
⊗ ψ−
)
ΨCA
+ =
√1 (ψ C
+
2
A
C
A
⊗ ψ−
+ ψ−
⊗ ψ+
)
ΨCA
− =
√1 (ψ C
+
2
A
C
A
⊗ ψ−
− ψ−
⊗ ψ+
)
Ora per misurare S è opportuno cambiare la base dello spazio di Hilbert HC ⊗ HA , dalla
base B1 alla base B2 . Significa quindi esprimere i vettori di B1 rispetto a B2 nel modo
seguente:
C
A
(1) ψ+
⊗ ψ+
si può esprimere come
√1 (ΦCA
+
2
√1 (ΦCA
+
2
+ ΦCA
− ). Infatti
A
A
A
A
C
A
1 C
1 C
1 C
1 C
+ ΦCA
− ) = 2 ψ+ ⊗ ψ+ + 2 ψ− ⊗ ψ− + 2 ψ+ ⊗ ψ+ − 2 ψ− ⊗ ψ− = ψ+ ⊗ ψ+
Analogamente si possono esprimere
A
C
=
⊗ ψ−
(2) ψ+
A
C
(3) ψ− ⊗ ψ+ =
A
C
=
⊗ ψ−
(4) ψ−
√1 (ΨCA
+
2
1
CA
√ (Ψ
+
2
√1 (ΦCA
+
2
+ ΨCA
− )
− ΨCA
− )
CA
− Φ− )
Sostituendo i vettori (1), (2), (3), (4) con quelli trovati si ottiene
α
√
2
h
+ √β2
√1 (ΦCA
+
2
h
B
+ ΦCA
− ) ⊗ ψ+ +
√1 (ΨCA
+
2
−
ΨCA
− )
⊗
B
ψ+
√1 (ΨCA
+
2
+
B
+ ΨCA
− ) ⊗ ψ−
√1 (ΦCA
+
2
−
ΦCA
− )
⊗
i
B
ψ−
i
B
CA
B
CA
B
CA
B
= α2 (ΦCA
+ ⊗ ψ+ + Φ− ⊗ ψ+ + Ψ+ ⊗ ψ− + Ψ− ⊗ ψ− )
B
CA
B
CA
B
CA
B
+ β2 (ΨCA
+ ⊗ ψ+ − Ψ− ⊗ ψ+ + Φ+ ⊗ ψ− − Φ− ⊗ ψ− )
B
B
B
B
1 CA
1 CA
1 CA
= 12 ΦCA
+ ⊗ αψ+ + 2 Φ− ⊗ αψ+ + 2 Ψ+ ⊗ αψ− + 2 Ψ− ⊗ αψ−
B
B
B
B
1 CA
1 CA
1 CA
+ 21 ΨCA
+ ⊗ βψ+ − 2 Ψ− ⊗ βψ+ + 2 Φ+ ⊗ βψ− − 2 Φ− ⊗ βψ−
Mettendo in evidenza gli stati della base di Bell, si ottiene
B
B
B
B
B
B
B
B
1 CA
1 CA
1 CA
Θ = 12 ΦCA
+ ⊗(αψ+ +βψ− )+ 2 Φ− ⊗(αψ+ −βψ− )+ 2 Ψ+ ⊗(αψ− +βψ+ )+ 2 Ψ− ⊗(αψ− −βψ+ )
Ora Alice compie la misura di Bell sul sistema formato dalle particelle A e C nello
stato intrecciato Θ. La misura può dare solo quattro risultati (gli autovalori {λi }4i=1 ),
in modo equiprobabile, ossia con probabilità 14 . Nella tabella sottostante sono illustrati
gli autovalori che si osservano, con i rispettivi autovettori.
Per esempio se Alice osserva λ1 , per il postulato della misura ideale, il sistema formato
dalle particelle A e C è (istantaneamente dopo la misura) nello stato ΦCA
+ e conseguenteB
B
mente il sistema formato da B è (pure istantaneamente) nello stato αψ+
+ βψ−
.
4.5 Il Teletrasporto
69
Risultato della misura Stato di AC dopo la misura Stato di B dopo la misura Probabilità
1
B
B
+ βψ−
λ1
ΦCA
ψ B = αψ+
+
4
1
B
B
B
−
βψ
λ2
ΦCA
ψ
=
αψ
−
−
+
4
1
B
B
B
λ3
ΨCA
ψ
=
αψ
+
βψ
+
−
+
4
1
CA
B
B
B
λ4
Ψ−
ψ = αψ− − βψ+
4
Tabella 4.2: Risultati e conseguenze della misura di Bell.
Ricordo che lo stato ϕ della particella C da teletrasportare alla particella B è
ϕ = αψ+ + βψ− . Quindi dobbiamo fare in modo che ψ B = ϕ. Come vediamo dalla
tabella, dopo la misura di Bell lo stato ψ B della particella B è uno dei quattro vettori
indicati. Analizziamo le varie situazioni:
1. Se Alice osserva l’autovalore λ1 , il sistema formato dalle particelle in suo posB
B
sesso è ΦCA
+ e il sistema formato dalla particella B di Bob è nello stato αψ+ + βψ− che
è proprio lo stato ϕ che si vuole teletrasportare. Bob però non conosce il risultato
della misura che ha operato Alice e ha quindi una conoscenza solo di tipo statistico
sullo stato del suo sistema (particella B), ossia sa che con probabilità 41 il suo sistema è
B
B
B
B
nello stato αψ+
+ βψ−
, con probabilità 14 il suo sistema è nello stato αψ+
− βψ−
, ecc
(v. tabella 4.2). Ciò corrisponde a un’informazione di tipo parziale, ovvero a uno stato
misto.
Alice deve perciò inviare un messaggio a Bob che gli comunichi se ha
osservato l’autovalore λ1 . Fra breve torneremo sulla questione dello scambio di
informazioni fra Alice e Bob.
2. Se Alice osserva un autovalore λi 6= λ1 , il sistema formato dalle particelle in
e il sistema formato
suo possesso è uno degli altri tre stati di Bell diversi da ΦCA
+
B
B
dalla particella B di Bob non è nello stato αψ+ + βψ− , ossia lo stato ϕ che si vuole
teletrasportare. Bob dovrà quindi intervenire sulla particella, correggendone lo stato.
Questa operazione è deterministica ed è data da una matrice unitaria U , come quelle
usate per l’evoluzione temporale di uno stato.
Calcoliamo ora quali sono questi operatori unitari U che Bob dovrà far agire sul suo
stato ψ B .
B
B
• Se Alice osserva λ2 , lo stato ψ B diventa αψ+
− βψ−
. Associamo a questo autovalore
la trasformazione U2 , quindi deve valere
!
!
!
(
)
a
b
α
α
a
=
1,
b
=
0
U2 ψ B = ϕ ⇐⇒
=
⇐⇒
c d
−β
β
c = 0, d = −1
Perciò
U2 =
1 0
0 −1
!
4.5 Il Teletrasporto
70
B
B
• Se Alice osserva λ3 , lo stato ψ B diventa αψ−
+ βψ+
. Associamo a questo autovalore
la trasformazione U3 , quindi deve valere
!
!
!
(
)
α
a
=
0,
b
=
1
a
b
β
U3 ψ B = ϕ ⇐⇒
=
⇐⇒
c d
α
β
c = 1, d = 0
Perciò
U3 =
0 1
1 0
!
B
B
. Associamo a questo autovalore
− βψ+
• Se Alice osserva λ4 , lo stato ψ B diventa αψ−
la trasformazione U4 , quindi deve valere
!
!
!
(
)
a
b
−β
α
a
=
0,
b
=
1
U4 ψ B = ϕ ⇐⇒
=
⇐⇒
c d
α
β
c = −1, d = 0
Perciò
U4 =
0 1
−1 0
!
• Nella situazione 1 l’operatore unitario è ovviamente
!
1 0
U1 = I =
0 1
Anche in questa seconda situazione Alice deve comunque inviare un messaggio a Bob che gli comunichi quale dei tre autovalori λi ha osservato.
Alice deve quindi inviare un messaggio a Bob in ogni caso, e questo messaggio di 2 bits deve essere trasmesso attraverso un canale classico (per esempio
via radio o fibre ottiche). Vediamo ora qual è il messaggio che viene mandato. Nella
tabella sottostante sono elencati i vari casi possibili.
Risultato Bits associati che Alice invia
λ1
00
λ2
01
λ3
10
λ4
11
Trasformazione che Bob deve applicare
U1
U2
U3
U4
Dopo che Bob ha ricevuto il messaggio e con esso ha potuto correggere il suo stato,
il teletrasporto è concluso: lo stato ϕ è passato da dalla particella C alla
particella B.
4.5.4
Riepilogo
Nella tabella 4.3 sono riassunte le tappe del protocollo di teletrasporto.
4.5 Il Teletrasporto
Azione
Particelle correlate A e B
Stato di C
Interazione fra A e C
Misura di Bell su ϕC ⊗ ΦAB
+
Stato di B (dopo la misura)
71
Punto di vista di Alice
Punto di vista di Bob
B
B
A
A
B
B
A
A
ΦAB
ΦAB
+ = {ψ+ ⊗ ψ+ + ψ− ⊗ ψ− }
+ = {ψ+ ⊗ ψ+ + ψ− ⊗ ψ− }
C
C
ϕ = ϕC = αψ+
+ βψ−
C
AB
ϕ ⊗ Φ+
possibili risultati: λ1 , λ2 , λ3 , λ4
B
B
B
ψ = αψ± ± βψ∓ (solo uno dei 4)
-
Invio del risultato a Bob
Applicazione di U
Stato di B
canale classico
−→
λi
-
λi
Ui ψ B
ϕ = ϕB
Tabella 4.3: Schema riassuntivo del protocollo di teletrasporto.
4.5.5
Discussione
Nella modellizzazione abbiamo trattato la procedura che viene chiamata teletrasporto
deterministico, poiché Bob deve correggere lo stato ψ B , applicando uno degli operatori
Ui , ogni volta che Alice osserva un autovalore diverso da λ1 , ciò che accade con probabilità
3
. Questo metodo necessita, come visto prima, dello scambio di due bits di informazioni.
4
L’altra procedura è quella del teletrasporto probabilistico che si differenzia da quello
deterministico perché Alice invia un messaggio a Bob indicandogli solo se ha osservato
l’autovalore λ1 . In questo caso il teletrasporto ha esito positivo con probabilità 41 e tra
Alice e Bob viene scambiato un solo bit di informazione, ovvero “1” se il teletrasporto
ha avuto luogo (cioè Alice ha osservato λ1 ) oppure “0” nel caso contrario.
Alla base del teletrasporto ci sono le correlazioni quantistiche delle particelle
A, B e C, dovute agli stati intrecciati. Infatti è grazie alle particelle A e B correlate
fra loro che intrecciando lo stato di C con quello della coppia (A, B), si riesce a
influenzare lo stato di B, non collegato fisicamente con C. È importante sottolineare
che, per le leggi della meccanica quantistica35 , quando Alice effettua la misura di
Bell modifica lo stato Θ del sistema e quindi lo stato di C non è più ϕ, ossia quello
che si è teletrasportato. Ciò significa che la particella originale alla fine della procedura è “persa”. Perciò non c’è alcuna clonazione di particelle, o meglio di stati quantistici.
Ci si può chiedere se è veramente necessario lo scambio (classico) di informazioni
fra Alice e Bob, perché questa operazione ci impedisce di rendere il teletrasporto
istantaneo. Proviamo a vedere cosa succederebbe se si tralasciasse lo scambio di bits
fra i due. Serviamoci della tabella 4.3 indicata nel riepilogo. Visto che Alice sa che
le particelle A e B sono correlate, dopo aver compiuto la misura di Bell conosce con
certezza lo stato della particella di Bob. Però lo sa solo lei, poiché Bob, fino a quando
35
Per il postulato della misura ideale.
4.5 Il Teletrasporto
72
non riceve il messaggio da Alice, sa solamente che la matrice che deve applicare per
(eventualmente) correggere lo stato è U1 con probabilità 41 , U2 con probabilità 14 , e
analogamente per le altre due matrici. Bob si trova quindi di fronte a uno stato misto
del sistema formato dalla sua particella B. Solo quando Alice gli comunica il risultato
della sua misura, Bob può sapere con certezza in quale dei 4 stati ψ B è la sua particella e
agire quindi applicando l’operatore unitario U conveniente. Quindi, senza lo scambio
di un segnale classico, Bob può solamente tentare di indovinare quale delle quattro
matrici di correzione U deve applicare per ottenere lo stato ϕ da teletrasportare, ma
dopo aver applicato U non saprà mai con certezza se lo stato ψ B della sua
particella è quello esatto, fintanto che Alice non gli manda il messaggio
classico con cui Bob può verificare se la matrice Ui che ha usato è proprio
quella indicatagli.
Vediamo quindi che non è possibile teletrasportare una particella istantaneamente, poiché è necessario lo scambio di un’informazione classica di
almeno un bit, che come sappiamo dalla teoria della relatività non può
propagarsi più velocemente della luce.
4.5.6
Conclusioni
I principali concetti da osservare sono:
• Alla base del teletrasporto ci sono le correlazioni quantistiche.
• È fondamentale tenere presente la necessità dello scambio di un segnale
classico fra la stazione di invio e quella di ricezione, che limita la
velocità del teletrasporto a quella della luce.
• Lo scambio dell’informazione classica è di 2 bit nel caso del
teletrasporto deterministico o di 1 bits in quello probabilistico.
• Con il teletrasporto non si trasmette materia ma lo stato quantistico
della particella che si vuole inviare.
Vediamo infine quali sono le applicazioni future del teletrasporto:
• La realizzazione di computer quantistici , che sarebbero in grado di fattorizzare a
velocità esponenziale e cercare a velocità quadratica, rispetto a quelle dei computer
attuali [19].
• La possibilità di scambi di informazione sicuri al 100%: fra la stazione di invio
e quella di ricezione viene scambiato solo un segnale classico che non permette
a un estraneo che lo intercetta di risalire all’informazione (sotto forma di stato
quantistico) che si sta teletrasportando.
4.5 Il Teletrasporto
73
• Vista la sicurezza dello scambio di un’informazione, una possibile utilità è quella
dell’e-vote, ossia il voto elettronico via internet (in studio in alcuni comuni del
Canton Ginevra).
Capitolo 5
Conclusione
In sede di conclusione analizziamo gli aspetti innovativi introdotti dalla fisica quantistica
a partire dall’inizio del XX secolo.
Siamo per “natura” abituati a delle teorie classiche, ossia realistiche, locali e
deterministiche. Vediamo di discutere questi tre concetti, riallacciandoli a quanto
trattato nei capitoli precedenti.
Una grandezza fisica è detta reale (e quindi la teoria è realistica) quando, senza
disturbare in alcun modo un sistema, possiamo predire con certezza (cioè con probabilità
uguale ad uno) il suo valore. Nel capitolo 4.2, in cui è trattato l’interferometro di
Mach-Zehnder, abbiamo concluso che la particella si delocalizza: essa è solamente con
probabilità 12 in uno dei due cammino dell’interferometro e quindi non esiste una quantità
fisica reale associata a tale situazione. Possiamo solo affermare con certezza che essa è
potenzialmente in entrambi i cammini. Inoltre abbiamo visto che il cammino in cui
passa la particella e il suo risultato sono due informazioni complementari , ciò significa
che queste due osservabili non possono essere reali contemporaneamente. Questi due
esempi mostrano che le proprietà fisiche non possono sempre essere reali e quindi la
teoria quantistica in questo senso non è realistica.
Nel capitolo 4.4 dedicato all’interferometro di Franson, abbiamo concluso che le
correlazioni sono un fenomeno fondamentale della fisica quantistica, perché solo con
essa si possono descrivere in modo corretto. Infatti grazie al teorema di Bell abbiamo
escluso una loro spiegazione con delle teorie classiche, ovvero di tipo locale, introducendo
dei parametri supplementari, che sono chiamati variabili nascoste. Quindi la teoria
quantistica è di tipo non locale e conseguentemente una misura effettuata su una
particella influenza istantaneamente a distanza l’altra. Per questo motivo le correlazioni
sono una delle cause, per cui la fisica quantistica sconvolge la visione tradizionale
del mondo.
Per quanto riguarda il determinismo, abbiamo visto che l’evoluzione temporale degli
stati è un processo deterministico, invece quello di misura non è deterministico.
Come detto in una teoria classica si hanno sempre delle situazioni in cui l’evoluzione è
75
5. Conclusione
76
deterministica, perciò, come ipotizzato da Einstein, si potrebbe sostenere che la teoria
quantistica sia incompleta, perché mancherebbero dei parametri che la renderebbero
deterministica. Abbiamo però dimostrato con il teorema di Bell (v.cap. 4.4) che non
è possibile completare la teoria quantistica con dei parametri supplementari (variabili
nascoste). La teoria quantistica è quindi completa e il processo di misura è
oggettivamente indeterministico.
Leggiamo ora alcune citazioni di personaggi di spicco sul significato della fisica
quantistica, tratte da [22]:
• “La meccanica quantistica è la descrizione dettagliata del comportamento della materia e della luce, in particolare di ciò che accade a scala atomica. Nel micromondo
le cose non si comportano come in un’esperienza diretta, non si comportano come
delle onde, non si comportano come delle particelle, non si comportano come delle
nuvole, né come delle palle da biliardo, né come qualcosa che voi non abbiate mai
visto.” (R. Feymann)
• “La meccanica quantistica è la più stramba invenzione del genere umano, ma anche
una delle più meravigliose. E la bellezza della matematica sottostante la teoria
dei quanti ci fa capire che abbiamo scoperto qualcosa di molto importante.” (A.
Zeilinger)
• “La scoperta della fisica quantistica non solo ci mostra i limiti naturali della fisica
classica; ma, gettando nuova luce sul vecchio problema filosofico dell’oggettiva esistenza dei fenomeni, indipendentemente dalle nostre osservazioni, ci mette di fronte
a una situazione che la scienza della natura finora non aveva conosciuto.” (N. Bohr)
• “Einstein diceva che se la meccanica quantistica si fosse rivelata corretta, allora il
mondo avrebbe dovuto essere folle. Einstein aveva ragione: il mondo è folle.” (D.
Greenberger)
• “Bohr intuiva che la posizione di Einstein, se fosse stata presa sul serio, sarebbe
risultata in aperto contrasto con la meccanica quantistica. Ma fu il teorema di Bell
a materializzare questa contraddizione.” (A. Aspect)
• “Gli elementi della realtà di Einstein non esistono. Non si può dare alcuna spiegazione, nei termini di un mondo reale oggettivo, della splendida danza a due mostrata
dalle particelle. Le particelle non fanno quello che fanno semplicemente per come
sono fatte; fanno quello che fanno per via della magia quantistica.” (M. Horne)
• “La teoria più fondamentale, a nostra disposizione al momento, ha una veste
probabilistica, e non deterministica.” (D. Bohm)
5. Conclusione
77
Da queste osservazioni possiamo affermare che
La visione classica del mondo, ossia realista, determinista e locale della
scienza della fine del 1800 non può più essere mantenuta alla luce delle
conoscenze attuali.
La fisica quantistica ha rivoluzionato la visione del mondo formatasi nel corso dei secoli
antecedenti il XX, introducendo queste tre nuove caratteristiche che sono quindi delle proprietà fondamentali della natura. A prima vista esse possono assumere una connotazione
negativa, perché si pensa che un fenomeno non locale, non reale e indeterministico rappresenti uno svantaggio sul piano della conoscenza del sistema fisico studiato; ma invece
questi aspetti si rivelano indispensabili per poter realizzare certi obiettivi, come dimostrato con il teletrasporto, che sarebbero altrimenti irraggiungibili. In altre parole, le
esperienze fatte per dimostrare i fondamenti della fisica quantistica si rivelano una risorsa
che permette la realizzazione di nuove tecnologie, che sarebbero classicamente impossibili da attuare. Queste tre differenze fondamentali fra la teoria di tipo classico e quella
di tipo quantistico, hanno fatto nascere molte discussioni nella comunità scientifica sul
significato di questa diversa visione del mondo, poiché sono sorti molti problemi sull’interpretazione della fisica quantistica ad un livello metafisico. Ci sono parecchie
interpretazioni diverse, ma tutte sono in accordo con le leggi della meccanica quantistica
[23]. Però questa è un’altra storia . . .
Appendice A
Esempio classico: il valore medio, lo
stato misto e lo stato di conoscenza
assoluta
Per comprendere meglio il ruolo del valore medio e degli stati in un sistema illustro qui
un esempio preso dalla fisica classica. Sottolineo che in fisica classica certi stati della
meccanica quantistica non esistono neppure; questo esempio serve per capire meglio la
terminologia.
Una particella, rappresentata dall’osservabile posizione X, si sposta nell’intervallo [0, 1] e
può prendere i solo valori: x0 = 0, x1 = 13 , x2 = 23 , x3 = 1. Abbiamo quindi che l’insieme
Γ dei valori dell’osservabile “di base” X è Γ = {x0 , x1 , x2 , x3 }.
(1) Possiamo avere che la particella si trova alla posizione x2 , ovvero X = x2 con probabilità p2 = 1 (ciò significa che lo stato è di conoscenza assoluta 1 ) inoltre pi = 0 se
i 6= 2. Il valore medio della posizione è quindi:
hXi =
3
X
xλ pλ = x0 · 0 + x1 · 0 + x2 · 1 + x3 · 0 = x2 =
λ=0
2
3
(2) Se invece sapessimo solamente che la particella ha una probabilità p0 = 33.3% = 13
di trovarsi in X = x0 , p3 = 66.6% = 23 di essere in X = x3 e p1 = p2 = 0. In questo caso
abbiamo a che fare con uno stato misto poichè l’osservatore (noi) ha solo una conoscenza
di tipo statistico sul sistema, allora in questo caso il valore medio è:
hXi =
3
X
2
2
1
xλ pλ = x0 + 0x1 + 0x2 + x3 =
3
3
3
λ=0
Come si vede i valori medi nei due casi (1) e (2) sono uguali, ma gli stati del sistema sono
ben diversi. Perciò valori medi uguali non implicano lo stesso stato.
1
In fisica classica gli stati puri equivalgono agli stati stati di conoscenza assoluta per
tutte le osservabili, ossia rappresentano entrambi una conoscenza assoluta del sistema.
79
Appendice B
Alcune proprietà dello spazio di
Hilbert H = C2 e delle matrici
• Se Pψ rappresenta il proiettore ortogonale sulla direzione definita dal vettore normalizzato ψ ∈ C2 , allora, rispetto alla base canonica, la matrice di Pψ si calcola nel
modo seguente
!
|ψ1 |2 ψ1 ψ¯2
Pψ =
ψ2 ψ¯1 |ψ2 |2
• Il prodotto scalare di due vettori ψ ∈ C2 e ϕ ∈ C2 , rispetto alla base canonica, è
espresso nel modo da
2
X
ψ̄i ϕi
(ψ, ϕ) =
i=1
• La norma di un vettore ψ ∈ C2 è data da
q
p
||ψ|| = (ψ, ψ) = ψ¯1 ψ1 + ψ¯2 ψ2
• Il prodotto C di due matrici A e B, che non è commutativo, è dato da
cij =
n
X
aik bkj
k=1
dove cij sono gli elementi della matrice C = AB, aik sono gli elementi della matrice
A e bkj gli elementi della matrice B.
• Il prodotto scalare tra due vettori ψ1 ⊗ ψ2 e ϕ1 ⊗ ϕ2 appartenenti allo spazio di
Hilbert H = C2 ⊗ C2 è definito da
(ψ1 ⊗ ψ2 , ϕ1 ⊗ ϕ2 ) = (ψ1 , ϕ1 )(ψ2 , ϕ2 )
• La norma di un vettore ψ1 ⊗ ψ2 ∈ C2 ⊗ C2 è data da
||ψ1 ⊗ ψ2 || = ||ψ1 || ||ψ2 ||
81
Bibliografia
Introduzione:
[1] B. Greene, L’universo elegante, Einaudi edizioni (2003)
Struttura della meccanica quantistica:
[2] C. Ferrari, Introduzione alla meccanica quantistica: un approccio moderno, Liceo di
Locarno (2004),
wwwlilo.lic.ti-edu.ch/Liceo_di_Locarno/intranetutenti/Siti_docenti/ferrari/index.html
[3] A. Shimony, I fondamenti concettuali della meccanica quantistica, in La nuova fisica,
a cura di P. Davies, Ed. Bollati Boringhieri (1992).
Interferenze a una particella:
[4] V. Scarani, Initiation à la physique quantique, Vuibert (2003)
[5] C. Piron, Mécanique quantique: Bases et applications, PPUR (1990)
Interferenze a due particelle e Teorema di Bell:
[6] C. Ferrari, Le variabili nascoste e il teorema di Bell, Liceo di Locarno (2004),
wwwlilo.lic.ti-edu.ch/Liceo_di_Locarno/intranetutenti/Siti_docenti/ferrari/index.html
[7] A. Aspect, P. Grangier, G. Roger, Experimental Realization of Einstein-PodolskyRose-Bohm Gedankenexperiment: A New Violation of Bell’s Inequalities, Phys. Rev.
Lett. 49, 91 (1982).
[8] A. Aspect, J. Dalibard, G. Roger, Experimental Test of Bell’s Inequalities Using
Time-Varying Analyzers, Phys. Rev. Lett. 49, 1804 (1982).
[9] A. Aspect, Bell’s Inequalities test: more ideal than ever, Nature 398, 189 (1999).
[10] W. Tittel, J. Brendel, H. Zbinden, N. Gisin, Violation of Bell Inequalities by Photons
More Than 10 km Apart, Phys. Rev. Lett. 81, 3563 (1998).
[11] N. Brunner, V. Scarani, M. Wegmueller, M. Legré, N. Gisin, Direct Measurement
of Superluminal Group Velocity and Signal Velocity in an Optical Fiber, Phys. Rev.
Lett. 90, 203902-1 (2004).
83
BIBLIOGRAFIA
84
Teletrasporto:
[12] M. Murianni, Più veloce della luce, Newton, numero 2 - Febbraio 2004.
[13] Il teletrasporto funziona, ma non come in Star Trek, sito internet del mensile Newton
(9.8.2004),
www.newton.rcs.it/PrimoPiano/News/2004/08_Agosto/9/teletrasporto.shtml
[14] Teleportation exits realm of sci-fi, sito internet di EETIMES (27.9.2004)
www.eet.com/article/showArticle.jhtml?articleId=44300008
[15] C. H. Bennet, G. Brassard, C. Crépeau, R. Jozsa, A. Peres, W. K. Wootters, Teleporting an Unknown Quantum State via Dual Classical and EPR Channels, Phys.
Rev. Lett. 70, 1895 (1993).
[16] Quantum Optics Group (California Institute of Technology), Quantum Teleportation,
sito internet (25.9.04) www.its.caltech.edu/~qoptics/teleport.html
[17] M.D. Barrett, J. Chiaverini, T. Schaetz, J. Britton, W.M. Itano, J.D. Jost, E.
Knill, C. Langer, D. Leibfried, R. Ozeri, D.J. Wineland, Deterministic quantum
teleportation of atomic qubits, Nature 429, 737 - 739 (2004).
[18] I. Marcikic, H. de Riedmatten, W. Tittel, H. Zbinden, N. Gisin, Long-distance
teleportation of qubits at telecommunication wavelengths, Nature 421, 509 (2003).
[19] Per le applicazioni del teletrasporto a PC quantistici vedi
www.research.ibm.com/quantuminfo
Conclusione:
[20] O. Nicrosini, Paradosso EPR e Teorema di Bell, Quanderni di fisica teorica (1991).
[21] C. Ferrari, L’argomento di Einstein, Podolsky e Rosen (EPR), Liceo di Locarno
(2004),
wwwlilo.lic.ti-edu.ch/Liceo_di_Locarno/intranetutenti/Siti_docenti/ferrari/index.html
[22] Amir D. Aczel, Entanglement, Raffaello Cortina Editore (2004).
[23] A. Zeilinger, On the Interpretation and Philosophical Foundation of Quantum
Mechanics, Helsinki University Press (1996).




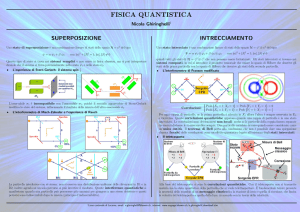
![[20120717] G.Giuni - La particella di Dio](http://s1.studylibit.com/store/data/007496773_1-f092519b9bc101b4085a20f32004c93f-300x300.png)






