Distanza di Mahalanobis
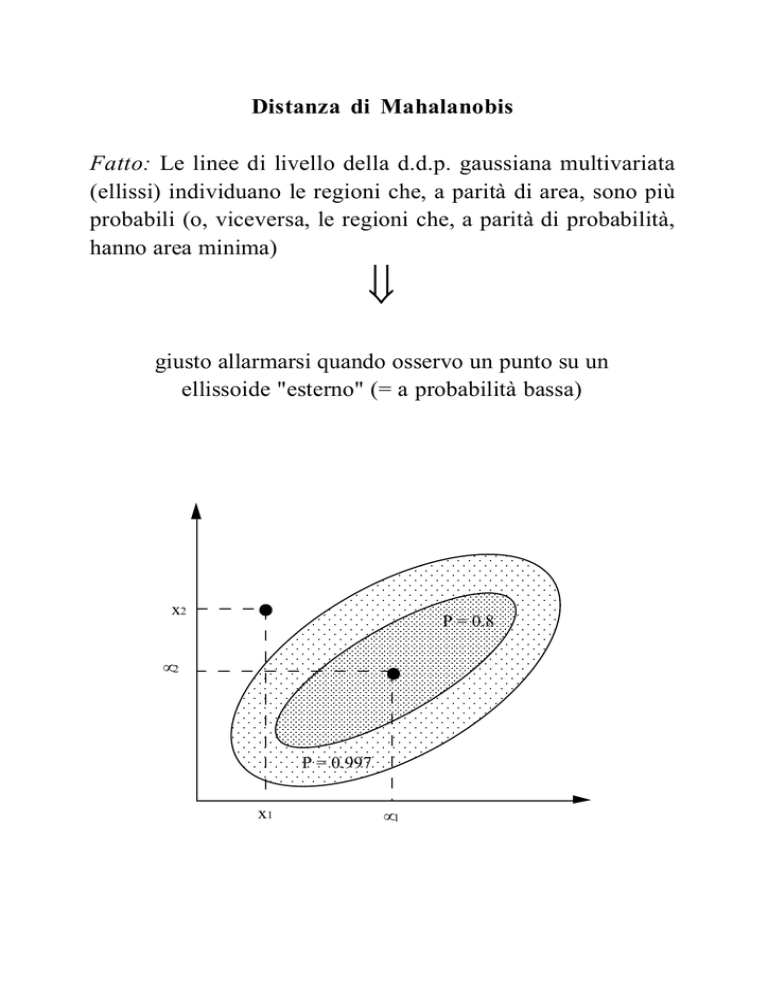
Fatto: Le linee di livello della d.d.p. gaussiana multivariata
(ellissi) individuano le regioni che, a parità di area, sono più
probabili (o, viceversa, le regioni che, a parità di probabilità,
hanno area minima)
⇓
giusto allarmarsi quando osservo un punto su un
ellissoide "esterno" (= a probabilità bassa)
x2
P = 0.8
µ2
P = 0.997
x1
µ1
Osservazione: Un punto è tanto più probabile quanto più
l'ellisse sui cui giace è vicina al centro (le cui coordinate sono
i valori medi [µ 1 ,…, µ n ]' = E[x]).
Idea: Introduco una misura di distanza ("improbabilità") che
cresce a mano a mano che x si sposta su ellissi più esterne
Distanza di Mahalanobis:
Q := (x- µ )' Σ -1 (x- µ )
Σ = Var[x] =
σ12
σ21
…
σn1
σ12 … σ1n
σ22 … σ2n
… …
σn2 …
…
σn2
Osservazioni:
•
Caso particolare: n = 2, r = 0
(x 1 - µ 1 ) 2 (x 2 - µ 2 ) 2
Q :=
+
σ12
σ22
x2
B
A
C
µ2
µ1
x1
Peso di meno le variabili più disperse
•
Q è l'esponente della gaussiana multivariata:
f X (x) =
1
(2π)ndet(Σ)
√
e
-
(x- µ )' Σ -1 (x- µ )
2
L'ellisse di controllo
Proprietà: Q = (x- µ )'Σ -1(x- µ ) ~ χ n2
Ipotesi: n = 2
Ellisse di controllo: Fissato α, trovo χ2α,n e traccio l'ellisse di
equazione (x-µ )'Σ -1(x-µ ) = χ 2α,n. Segnalo un fuori controllo
quando un punto cade fuori.
UCL
LCL
UCL
LCL
Svantaggi:
•
Si perde la sequenza temporale dei punti.
•
Cosa fare per n > 2?
La carta χ 2
Idea: Per ogni campione x(t), calcolo
Q(t) = (x(t)-µ )'Σ -1(x(t)-µ )
e lo riporto su una carta apposita.
Limite di controllo: UCL = χ 2α ,n
UCL
1
3
5
7
9
11
13
15
17
19
21
23
Sample number
Carta T 2 (Hotelling 1947)
Nella pratica, µ e Σ non sono noti, ma disponiamo di
¯ e Σ̂.
stime X
Punti da disegnare:
¯ )'Σ̂-1(x(t) - X
¯)
T 2 (t) = (x(t) - X