Attività 1. Grafico di parabole con equazione del tipo y = ax
2
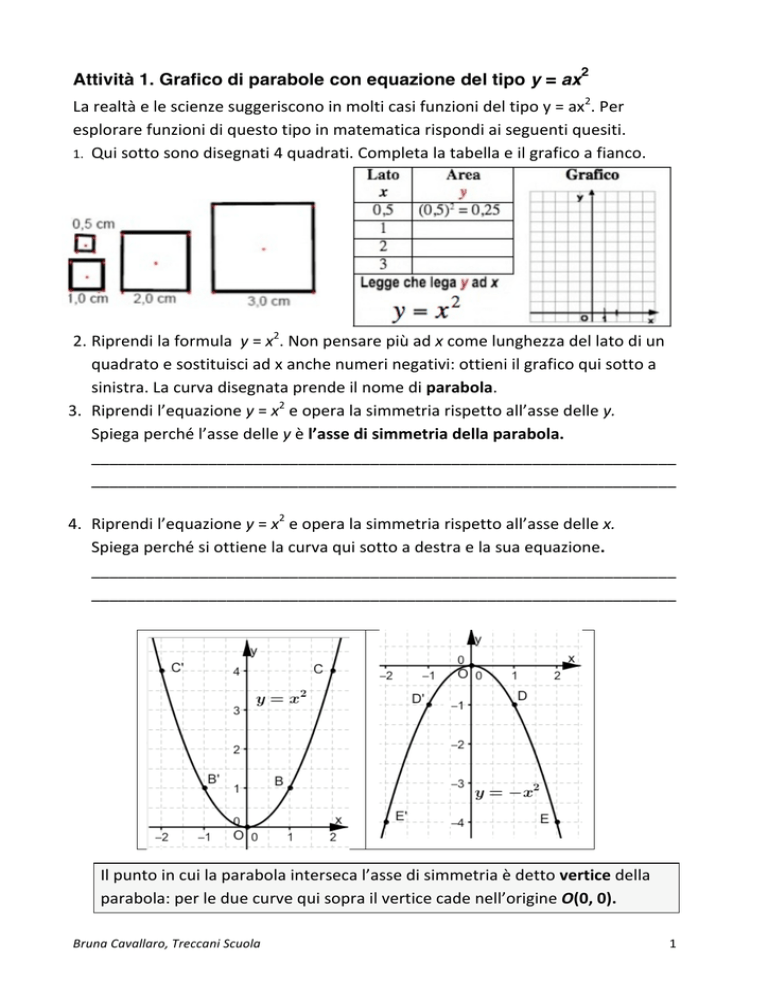
La realtà e le scienze suggeriscono in molti casi funzioni del tipo y = ax2. Per esplorare funzioni di questo tipo in matematica rispondi ai seguenti quesiti. 1. Qui sotto sono disegnati 4 quadrati. Completa la tabella e il grafico a fianco.
2
2. Riprendi la formula y = x . Non pensare più ad x come lunghezza del lato di un quadrato e sostituisci ad x anche numeri negativi: ottieni il grafico qui sotto a sinistra. La curva disegnata prende il nome di parabola. 3. Riprendi l’equazione y = x2 e opera la simmetria rispetto all’asse delle y. Spiega perché l’asse delle y è l’asse di simmetria della parabola. _________________________________________________________________ _________________________________________________________________ 4. Riprendi l’equazione y = x2 e opera la simmetria rispetto all’asse delle x. Spiega perché si ottiene la curva qui sotto a destra e la sua equazione. _________________________________________________________________ _________________________________________________________________ Il punto in cui la parabola interseca l’asse di simmetria è detto vertice della parabola: per le due curve qui sopra il vertice cade nell’origine O(0, 0). Bruna Cavallaro, Treccani Scuola 1 5. Apri il file ‘Parabola1_Geogebra_Scheda1’; compare un finestra grafica, dove sono disegnate: - In nero, la parabola di equazione y = x2, che rimane fissa; - in rosso, la parabola d’equazione y = ax2 e puoi muovere lo slider blu a destra per variare il coefficiente a. Muovi lo slider e osserva i grafici per rispondere ai sequenti quesiti: I. Nella tabella qui sotto sono disegnate le parabole d’equazione Completa la tabella per associare ad ogni grafico la sua equazione. Equazione:
Equazione:
Equazione:
Equazione:
Equazione:
Equazione:
II. Scrivi vero (V) o falso (F) vicino ad ognuna delle seguenti affermazioni. Affermazione
Tutte le parabole d’equazione y = ax2 hanno il vertice O (0, 0)
Tutte le parabole d’equazione y = ax2 hanno l’asse di simmetria d’equazione y = 0
Per tutte le parabole d’equazione y = ax2 il vertice è il punto più basso
Solo se a > 0 una parabola d’equazione y = ax2 rivolge la concavità verso l’alto
Solo se a < 1 una parabola d’equazione y = ax2 è ‘più larga’ della curva
d’equazione y = x2.
Se a = 0, la parabola va a coincidere con l’asse delle x.
Bruna Cavallaro, Treccani Scuola V/F
2












