disequazioni irrazionali
logaritmi
log 1 x log a x
a
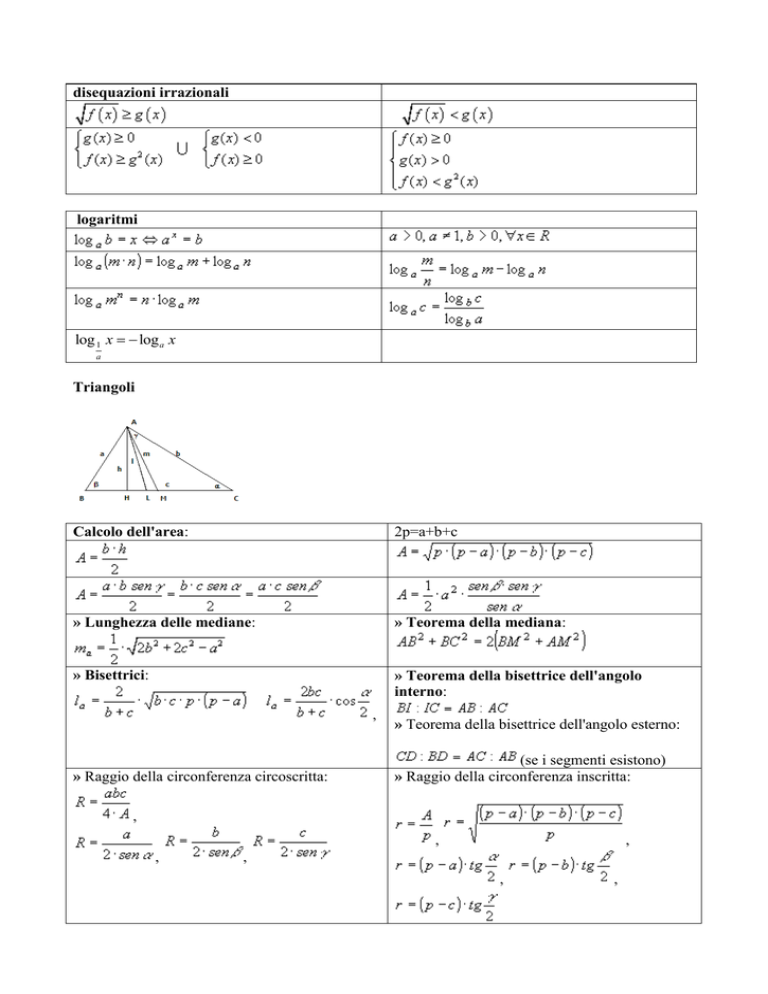
Triangoli
Calcolo dell'area:
2p=a+b+c
» Lunghezza delle mediane:
» Teorema della mediana:
» Bisettrici:
» Teorema della bisettrice dell'angolo
interno:
,
» Raggio della circonferenza circoscritta:
» Teorema della bisettrice dell'angolo esterno:
(se i segmenti esistono)
» Raggio della circonferenza inscritta:
,
,
,
,
,
,
,
» Altezze:
,
» Teorema dei seni (o di Eulero)
In un triangolo è costante il rapporto tra la
misura di un lato e il seno dell'angolo opposto:
» Teorema della corda
In un triangolo il rapporto tra la misura di un
lato e il seno dell'angolo opposto è uguale al
diametro della circonferenza circoscritta:
= 2r
» Teorema del coseno (o di Carnot)
» Formule di Briggs:
In un triangolo il quadrato di un lato è uguale alla
somma dei quadrati degli altri due diminuita del
prodotto di questi due lati per il coseno
dell'angolo fra essi compreso:
,
,
,
,
,
.
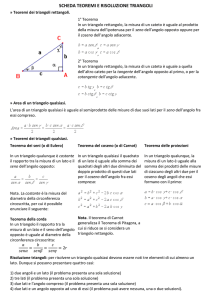
Triangoli rettangoli
» Teorema di Pitagora: .
» Primo teorema di Euclide:
;
» Secondo teorema di Euclide:
In un triangolo rettangolo l'altezza è media
proporzionale tra le proiezioni dei due cateti
» Proprietà della mediana:
sull'ipotenusa.
Calcolo dell'area:
,
» Misura dell'altezza noti i lati:
» 1° teorema sui triangoli rettangoli:
» 2° teorema sui triangoli rettangoli:
In un triangolo rettangolo la misura di un cateto è
uguale al prodotto dell'ipotenusa per il seno
dell'angolo opposto o per il coseno dell'angolo
adiacente
In un triangolo rettangolo la misura di un cateto
è uguale al prodotto dell'altro cateto per la
tangente dell'angolo opposto o per la cotangente
dell'angolo adiacente
,
» Calcolo dell’area quadrilatero
(diagonale per diagonale per il seno
dell’angolo compreso diviso 2)
,
Cerchio
Raggio = r
Lunghezza della circonferenza:
Area del cerchio:
Lunghezza dell'arco:
Area del settore circolare:
Area del semicerchio:
Area del
quadrante:
Area della corona circolare:
Area del segmento circolare: si trova come
differenza fra l'area di un settore e l'area di un
triangolo.
Solidi
Le figure geometriche solide possono essere suddivise in due gruppi:
quelli la cui superficie è formata da soli poligoni detti poliedri, e quelli la cui superficie è curva
detti solidi rotondi.
Un poliedro è un solido limitato da più poligoni posti su piani diversi e tali che ogni lato è
comune a due soli di essi.
Tra le facce gli spigoli e i vertici di un poligono sussiste la relazione di Eulero: f + v = s + 2