file

Concetti chiave e regole
I triangoli rettangoli
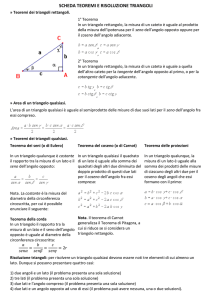
I triangoli rettangoli godono delle proprietà enunciate dai seguenti teoremi:
l
l
Primo teorema. In ogni triangolo rettangolo la misura di un cateto è uguale al
prodotto della misura dell’ipotenusa per
– il seno dell’angolo opposto:
b ¼ a sin c ¼ a sin – il coseno dell’angolo adiacente:
b ¼ a cos c ¼ a cos Secondo teorema. In ogni triangolo rettangolo la misura di un cateto è uguale al
prodotto della misura dell’altro cateto per
– la tangente dell’angolo opposto:
b ¼ c tan c ¼ b tan – la cotangente dell’angolo adiacente:
b ¼ c cotan c ¼ b cotan L’area di un triangolo e il teorema della corda
Le conseguenze immediate dei due precedenti teoremi sono le seguenti:
l
l
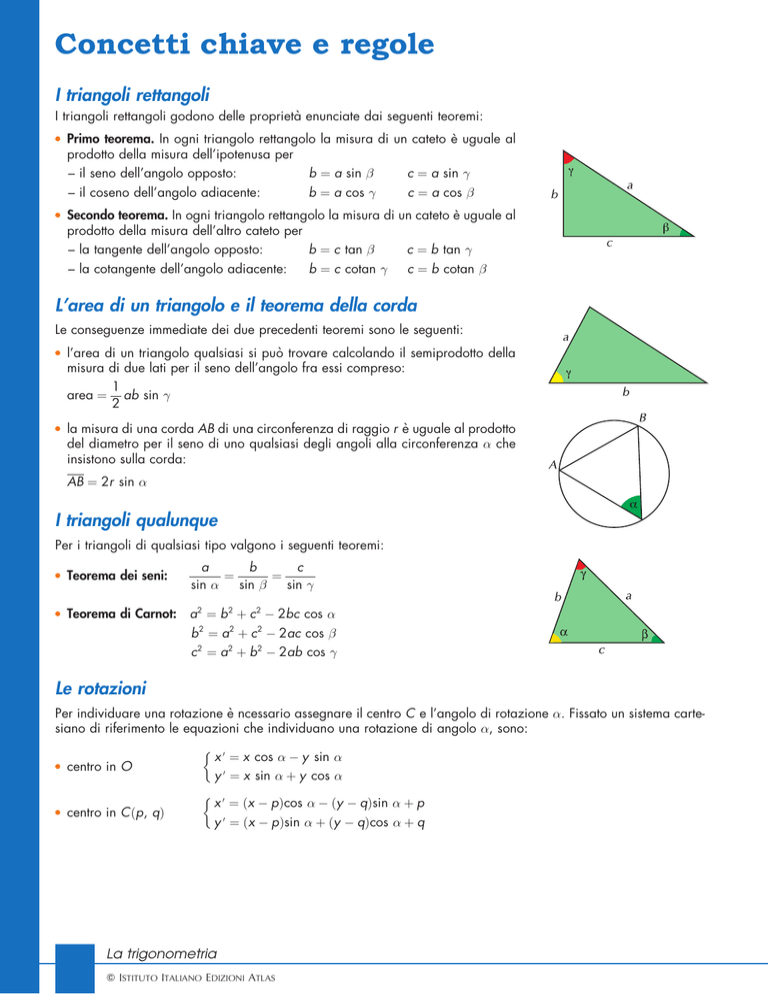
l’area di un triangolo qualsiasi si può trovare calcolando il semiprodotto della
misura di due lati per il seno dell’angolo fra essi compreso:
1
area ¼ ab sin 2
la misura di una corda AB di una circonferenza di raggio r è uguale al prodotto
del diametro per il seno di uno qualsiasi degli angoli alla circonferenza che
insistono sulla corda:
AB ¼ 2r sin I triangoli qualunque
Per i triangoli di qualsiasi tipo valgono i seguenti teoremi:
l
Teorema dei seni:
l
Teorema di Carnot:
a
b
c
¼
¼
sin sin sin a2 ¼ b 2 þ c2 2bc cos b 2 ¼ a2 þ c2 2ac cos c2 ¼ a2 þ b2 2ab cos Le rotazioni
Per individuare una rotazione è ncessario assegnare il centro C e l’angolo di rotazione . Fissato un sistema cartesiano di riferimento le equazioni che individuano una rotazione di angolo , sono:
l
centro in O
l
centro in Cðp, qÞ
x 0 ¼ x cos y sin y 0 ¼ x sin þ y cos x 0 ¼ ðx pÞcos ðy qÞsin þ p
y 0 ¼ ðx pÞsin þ ðy qÞcos þ q
La trigonometria
Q ISTITUTO ITALIANO EDIZIONI ATLAS