Teorema di Thévenin – esercizio n. 6
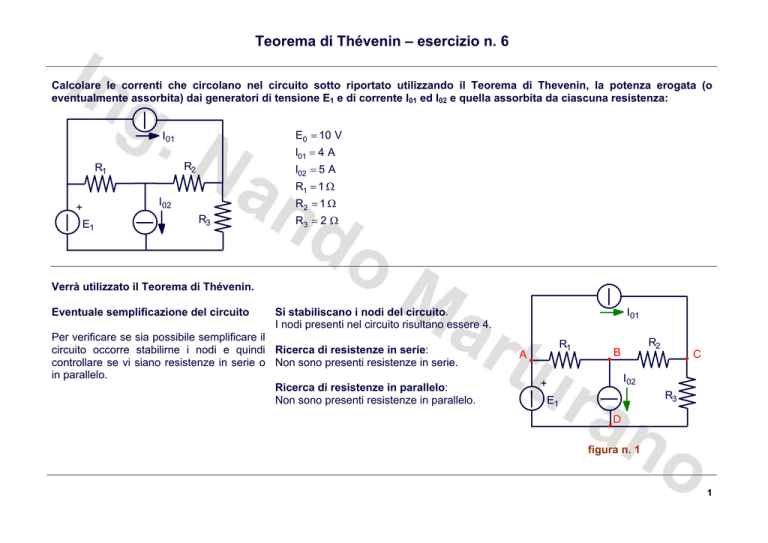
Calcolare le correnti che circolano nel circuito sotto riportato utilizzando il Teorema di Thevenin, la potenza erogata (o
eventualmente assorbita) dai generatori di tensione E1 e di corrente I01 ed I02 e quella assorbita da ciascuna resistenza:
E0 = 10 V
I01
I01 = 4 A
R2
R1
I02 = 5 A
R1 = 1 Ω
+
E1
R2 = 1 Ω
I02
R3
R3 = 2 Ω
Verrà utilizzato il Teorema di Thévenin.
Eventuale semplificazione del circuito
Si stabiliscano i nodi del circuito.
I nodi presenti nel circuito risultano essere 4.
Per verificare se sia possibile semplificare il
circuito occorre stabilirne i nodi e quindi Ricerca di resistenze in serie:
controllare se vi siano resistenze in serie o Non sono presenti resistenze in serie.
in parallelo.
Ricerca di resistenze in parallelo:
Non sono presenti resistenze in parallelo.
I01
R1
A
R2
B
C
I02
+
R3
E1
D
figura n. 1
1
Teorema di Thévenin – esercizio n. 6
Teorema di Thévenin:
Una rete elettrica lineare comunque complessa vista da due morsetti equivale ad un generatore reale di tensione.
La f.e.m. del generatore equivalente ETh corrisponde alla tensione a vuoto presente tra i due morsetti quando il carico è stato soppresso.
La resistenza interna del generatore RTh è quella vista dai terminali stessi a vuoto, dopo aver cortocircuitato i generatori di tensione ed
aperti quelli di corrente.
Si è scelto di calcolare la corrente nella resistenza R3.
Circuito per il calcolo di RTh:
Circuito per il calcolo di ETh = VDC:
Circuito elementare di Thévenin:
C
I01
RTh
A
R1
B
R2
C
R1
A
I0
B
C
ETh=VDC
I5
ETh=VDC
E0
D I02
La resistenza RTh vista da i terminali C e D è Si determina la corrente I1 utilizzando
l’equilibrio delle correnti al nodo B:
costituita dalla serie di R1 ed R2 .
RTh = RCD = R1 + R2 = 1 + 1 = 2 Ω
R3
+
I1
+
D
R2
I1 = I02 − I01 = 5 − 4 = 1 A
D
Calcolo della corrente I3:
I5 =
VCD
VTh
13
=
=
= 3,25 A
RTh + R3 RCD + R3 2 + 2
Per calcolare ETh=VDC si utilizza la strada
costituita dalle due resistenze R1 ed R2
ed E0:
VTh = VCD = E0 − R1 ⋅ I1 + R2 ⋅ I01 =
= 10 − 1⋅ 1 + 1⋅ 4 = 13 V
2
Teorema di Thévenin – esercizio n. 6
Nota: Il verso della d.d.p. tra i punti C e D a vuoto (senza la resistenza R5) che produce il generatore di tensione di Thévenin deve essere lo stesso
verso della d.d.p. che produce la rete da semplificare
Calcolo delle altre grandezze necessarie per Calcolo delle correnti: I1, I2 ed I0.
Calcolo delle d.d.p. VCA e VDB:
risolvere l’esercizio:
Per calcolare tali correnti è sufficiente
VCA = R2 ⋅ I2 − R1 ⋅ I1 =
Devono essere calcolate le correnti I1, I2 ed I0.
applicare il primo principio di Kirchhoff
= 1⋅ 0,75 − 1⋅ 4,25 = −3,50 V
ai nodi C, B ed A:
Devono essere calcolate le d.d.p. VCA e VDB,
VDB = −R3 ⋅ I3 + R2 ⋅ I2 =
necessarie per determinare le potenze erogate
= −2 ⋅ 3,25 + 1⋅ 0,75 = −5,75 V
nodo C:
dai generatori:
I2 = I01 − I3 = 4 − 3,25 = 0,75 A
I01
In conclusione tutte le correnti nel circuito
VCA
nodo B:
risultano essere :
I01 = 4 A
I1 = I02 − I2 = 5 − 0,75 = 4,25 A
R2
R1
B
C
A
I02 = 5 A
I0 I
I2
I0 = 8,25 A
1
nodo A:
+
I0 = I01 + I1 = 4 + 4,25 = 8,25 A
I1 = 4,25 A
VDB
R3
E0
I2 = 0,75 A
I
I
02
3
D
I = 3,25 A
3
3
Teorema di Thévenin – esercizio n. 6
Calcolo della potenza erogata dai generatori:
Calcolo delle potenze assorbite dalle resistenze;
Poiché, per i generatori di corrente I01 ed I02 il verso della corrente erogata ed il P = R ⋅ I 2 = 1⋅ 4,252 = 18,06 W
R1
1 1
verso della d.d.p. ai morsetti dei generatori sono discordi, allora tali generatori
2
2
assorbono potenza invece che erogarla e pertanto la loro potenza deve essere PR2 = R2 ⋅ I2 = 1⋅ 0,75 = 0,56 W
considera negativa.
PR3 = R3 ⋅ I3 2 = 2 ⋅ 3,252 = 21,12 W
PE0 = E0 ⋅ I0 = 10 ⋅ 8,25 = 82,50 W
PI01 = VCA ⋅ I01 = −3,5 ⋅ 4,00 = −14,00 W
Verifica potenze erogate ed assorbite:
PI02 = VDB ⋅ I02 = −5,75 ⋅ 5,00 = −28,75 W
PET = PE0 + PI01 + PI02 = 82,50 − 14,00 − 28,75 = 39,75 W
PRT = PR1 + PR2 + PR3 = 18,06 + 0,56 + 21,12 = 39,74 W
4