Esercizi vari per circuiti senza memoria

3UREOHPD
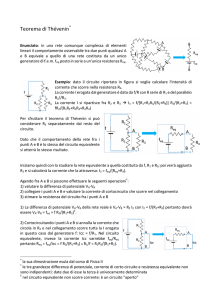
Determinare, mediante il teorema di Thevenin, la potenza erogata dal generatore V09 del circuito di Figura.
R2=10 Ω
A
E
R5=2 Ω
R6=4 Ω
B
I01
V09
V03
6A
28 V
30 V
F
D
R7=5 Ω
R8=10 Ω
C
I04=7 A
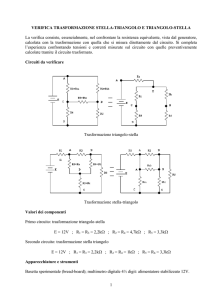
Calcolo della tensione del generatore del dipolo
equivalente:
Calcolo della resistenza del dipolo equivalente:
R2=10 Ω
R2=10 Ω
A
E
R5=2 Ω
R6=4 Ω
B
A
E0
I01
R5=2 Ω
E
R6=4 Ω
B
R7=5 Ω
C
V03
30 V
6A
Req
F
D
R7=5 Ω
R8=10 Ω
F
C
D
R8=10 Ω
I04=7 A
E0 = − 20 V
Req= 8 Ω
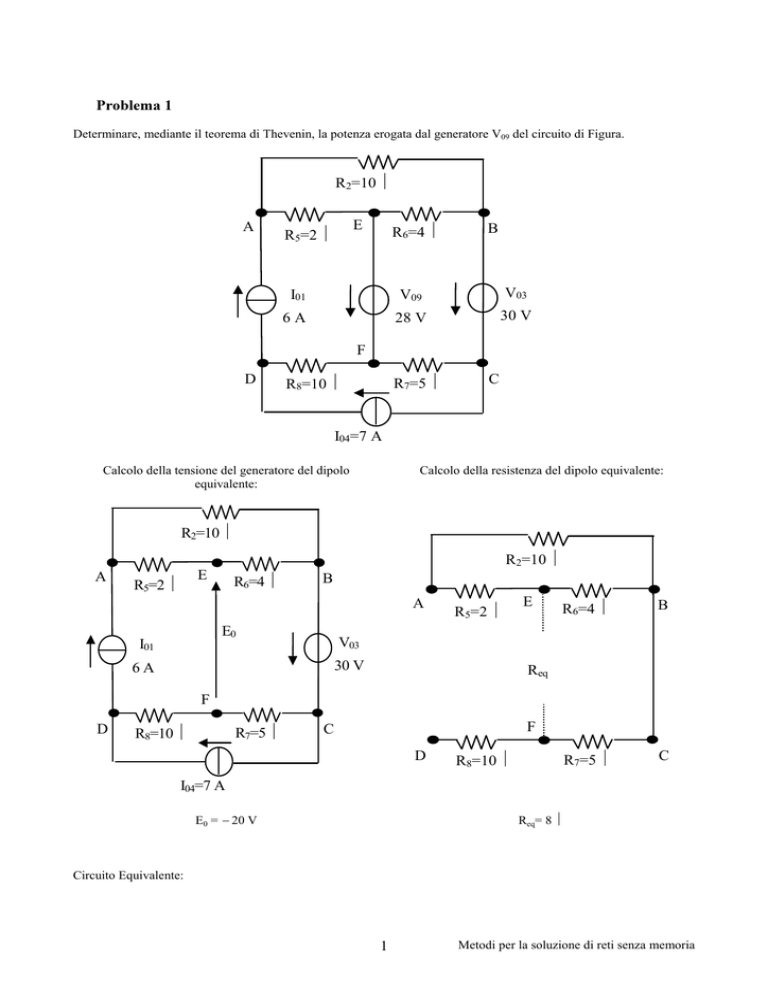
Circuito Equivalente:
1
Metodi per la soluzione di reti senza memoria
E
Req = 8 Ω
I9
V09
28 V
E0 = − 20 V
F
39 ( HURJDWD ) = 909 , 9 = 909
(909 + ( 0 )
= 28:
5HT
3UREOHPD
Determinare, aoperando le trasformazioni Triangolo-Stella la potenza dissipata dalla resistenza R5 del circuito di Figura
A
R3
100 Ω
V0
100 V
R1
100 Ω
C
D
R5
26 Ω
R2
40 Ω
R4
60 Ω
B
Circuito equivalente (Trasformazione Triangolo-Stella):
A
V0
100 V
RA
44.25 Ω
RD
11.5 Ω
RC
11.5 Ω
C
I4
R4
60 Ω
B
2
I2
D
R2
40 Ω
Metodi per la soluzione di reti senza memoria
2
9&'
( 54 , 4 − 5 2 , 2 ) 2
35 =
=
= 0.35:
55
55
3UREOHPD
Risolvere la rete di figura mediante il metodo delle correnti di maglia e verificare il bilancio di potenza
B
R5
V01= 170 V
V02=110 V
6Ω
I1
I5
R5=4 Ω
R1=10 Ω
A
I2
I4
R2=10 Ω
I6
D
R4=10 Ω
V3
C
R6=10 Ω
I3
I03=5 A
Scelta delle correnti di maglia
B
R5
V02
V01
I1
J1
J2
I5
R5
R1
A
I2
I4
R2
I6
D
R4
R6
C
VI3
J3
I3
I03
Sistema risolvente
3
Metodi per la soluzione di reti senza memoria
 51 - 1 + 55 (- 1 − - 2 ) + 54 (- 1 − - 3 ) = 901
 5 (- − - ) + 5 - + 5 (- − - ) = −9
1
2 2
6
2
3
02
 5 2

(
)
(
)
 54 - 3 − - 1 + 56 - 3 − - 2 = −9 ,3
- = ,
03
 3
Soluzione:
J1 = 9 A; J2 = −1 A; J3 = 5 A; VI3 = −20 V;
Correnti di ramo:
I1 = J1 = 9 A;
I2 = J2 = −1 A;
I3 = J3 = 5 A;
I4 = J3 − J1 = −4 A;
I5 = J1 − J2 = 10 A;
I6 = J2 − J3 = −6 A;
VAB=-80 V;
VBC=160 V;
VCA (VI3)=-20 V;
VAD=-40 V;
VBD=20 V;
VCD=-60 V;
Bilancio di Potenza:
− V01I1 + V02I2 + VI3I3 + R1I12 + R2I22 + R4I42 + R5I52 + R6I62 = 0
− 1530 − 110 − 100 + 810 + 10 + 160 + 400 + 360 = 0
3UREOHPD
Determinare la potenza dissipata sulla resistenza R4 delle rete di figura
A
R1
2Ω
R2
6Ω
R3
1Ω
R4
3Ω
I0
8A
R0
1Ω
E2
8V
E1
12V
B
50 , 0 / (50 + 51 ) + ( 2 / 52 + (3 / 53
= 8.73 V
1 / (50 + 51 ) + 1 / 52 + 1 / 53 + 1 / 54
Soluzione (teorema di Millman):
9 $% =
9
2
34 = 54 , 4 = $% = 25.4 W
54
2
4
Metodi per la soluzione di reti senza memoria