Teorema di Norton – esercizio n. 7
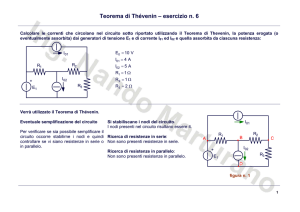
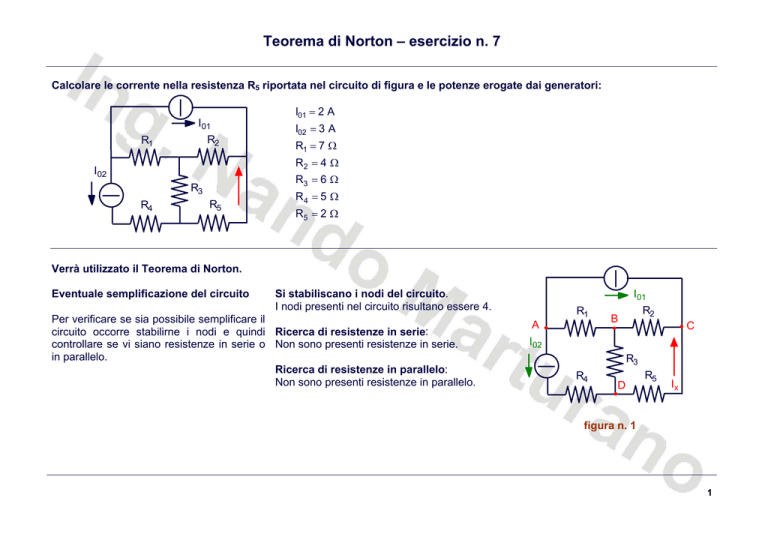
Calcolare le corrente nella resistenza R5 riportata nel circuito di figura e le potenze erogate dai generatori:
I01
R2
R1
I01 = 2 A
I02 = 3 A
R1 = 7 Ω
R2 = 4 Ω
I02
R3 = 6 Ω
R3
R4
R5
R4 = 5 Ω
R5 = 2 Ω
Verrà utilizzato il Teorema di Norton.
Eventuale semplificazione del circuito
Si stabiliscano i nodi del circuito.
I nodi presenti nel circuito risultano essere 4.
Per verificare se sia possibile semplificare il
circuito occorre stabilirne i nodi e quindi Ricerca di resistenze in serie:
controllare se vi siano resistenze in serie o Non sono presenti resistenze in serie.
in parallelo.
Ricerca di resistenze in parallelo:
Non sono presenti resistenze in parallelo.
I01
R1
A
R2
B
C
I02
R3
R4
D
R5
Ix
figura n. 1
1
Teorema di Norton – esercizio n. 7
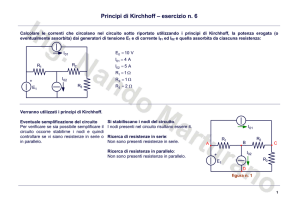
Teorema di Norton:
Una rete elettrica lineare comunque complessa vista da due morsetti equivale ad un generatore reale di corrente.
La corrente del generatore equivalente IN corrisponde alla corrente che fluisce tra i due morsetti quando il carico è stato cortocircuitato.
La resistenza interna del generatore RN è quella vista dai terminali stessi a vuoto, dopo aver cortocircuitato i generatori di tensione ed
aperto quelli di corrente.
Circuito per il calcolo di RN:
Circuito per il calcolo di IN = ICC:
Circuito elementare di Norton:
C
I01
R1
A
R1
R2
B
C
A
I02
D
R3
R4
RN
C
I1
R3
R4
R2
B
IN=ICC
I2
ICC
I3 D=C
La resistenza RN vista da i terminali D e C è Si noti come R2 ed R3 siano in parallelo e
che tale parallelo è attraversato dalla
costituita dalla serie di R2 ed R3 .
corrente I01 + I02 = 5 A. Pertanto:
R ⋅R
4⋅6
RN = RDC = R2 + R3 = 4 + 6 = 10 Ω
VCB = 2 3 ⋅ (I01 + I02 ) =
⋅ ( 3 + 2 ) = 12 V
R 2 + R3
4+6
V
12
di conseguenza:
I2 = CB =
=3 A
R2
4
Dall’equilibrio al nodo C si ricava che:
IN = ICC = I2 − I01 = 3 − 2 = 1 A
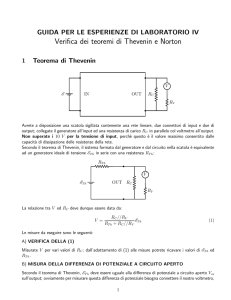
R5
I5
D
Per il calcolo della corrente I5 si utilizza la
regola del derivatore di corrente:
I5 = IN ⋅
RN
10
= 1⋅
= 0,83 Ω
RN + R5
10 + 2
2
Teorema di Norton – esercizio n. 7
Nota: Il verso della corrente che produce il generatore di corrente di Norton nel cortocircuito tra D e C deve essere lo stesso verso della corrente che
produce la rete da semplificare
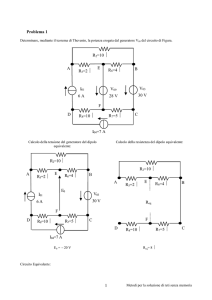
Calcolo delle grandezze necessarie per Calcolo delle correnti: I1 , I2 ed I3.
determinare le potenze erogate dai
Per calcolare tali correnti è sufficiente
generatori:
applicare il primo principio di Kirchhoff ai nodi
Per calcolare le potenze erogate dai A, C e D:
generatori occorrono le rispettive d.d.p. ad
nodo A:
essi applicati e cioè VCA e VHA:
I01
I1 = I01 + I02 = 2 + 3 = 5 A
VCA
R1
VHA
A
I02
H
B
C
nodo C:
I2 = I5 + I01 = 0,83 + 2 = 2,83 A
I2
I1
R4
R2
I5
R3
I3 D
R5
nodo D:
I3 = I02 − I5 = 3 − 0,87 = 2,17 A
Calcolo delle d.d.p. VCA e VHA:
VCA = R2 ⋅ I2 + R1 ⋅ I1 =
= 4 ⋅ 2,83 + 7 ⋅ 5 = 46,32 V
VHA = R4 ⋅ I02 + R3 ⋅ I3 + R1 ⋅ I1 =
= 5 ⋅ 3 + 6 ⋅ 2,17 + 7 ⋅ 5 = 63,02 V
In conclusione tutte le correnti nel circuito
risultano essere :
I01 = 2 A
I02 = 3 A
I1 = 5,00 A
I2 = 2,83 A
dove:
VCA = VCB + VBA = R2 ⋅ I2 + R1 ⋅ I1
I3 = 2,17 A
I5 = 0,83 A
VHA = VHD + VDB + VBA = R 4 ⋅ I02 + R3 ⋅ I3 + R1 ⋅ I1
Occorrono quindi le correnti: I1 , I2 ed I3.
3
Teorema di Norton – esercizio n. 7
Calcolo della potenza erogata dai generatori:
Calcolo delle potenze assorbite dalle resistenze;
Poiché, per i generatori di corrente I01 ed I02 il verso della corrente erogata ed il
verso della d.d.p. ai morsetti dei generatori sono concordi, allora tali generatori
erogano entrambi potenza.
PR1 = R1 ⋅ I12 = 7 ⋅ 5,002 = 175,00 W
PI01 = VCA ⋅ I01 = 46,32 ⋅ 2,00 = 92,64 W
PR3 = R3 ⋅ I3 2 = 6 ⋅ 2,172 = 28,25 W
PI02 = VDB ⋅ I02 = 63 ⋅ 3,00 = 189,00 W
PR2 = R2 ⋅ I22 = 4 ⋅ 2,832 = 32,04 W
PR4 = R 4 ⋅ I022 = 5 ⋅ 3,002 = 45,00 W
PR5 = R5 ⋅ I5 2 = 2 ⋅ 0,832 = 1,38 W
Verifica potenze erogate ed assorbite:
PET = PI01 + PI02 = 92,64 + 189,00 = 281,64 W
PRT = PR1 + PR2 + PR3 + PR4 + PR5 = 175,00 + 32,04 + 28,25 + 45,00 + 1,38 = 281,67 W
4