Esercizi
• 15/aprile 2013
ESEMPIO: Si consideri un punto materiale
1.
2.
3.
4.
posto ad un altezza h dal suolo,
posto su un piano inclinato liscio di altezza h,
attaccato ad un filo di lunghezza h il cui altro estremo è attaccato ad
un soffitto che dista h dal suolo: quando il filo si trova in posizione
verticale, il corpo sfiora il pavimento,
posto su una guida liscia di forma qualsiasi di altezza h
h
1)
2)
3)
4)
In tutti e quattro i casi, inizialmente il corpo si trova ad
altezza h, e viene abbandonato con velocità nulla da
questa posizione
Determinare la velocità con cui il corpo raggiunge il pavimento.
• Nel primo caso
– Agisce solo la forza peso (che è conservativa)
– Posso applicare la conservazione dell’energia
h
ΔE = 0 ⇒ Ei = Ef
K i + Ui = K f + Uf
Ki = 0
U i = mgh
K f = 12 mv 2f
Uf = 0
2
0 + mgh = 12 mv f + 0
v f = 2gh
L’energia potenziale iniziale viene
trasformata in energia cinetica
Abbiamo scelto il pavimento come
punto di riferimento ed assegnato
al pavimento energia potenziale
nulla
•
Nel secondo caso agiscono
– la forza peso (P) , che è conservativa,
– la reazione vincolare (N) del piano inclinato,
• (Solo la componente normale, perché per ipotesi il piano è liscio)
•
Possiamo applicare la relazione lavoro energia:
ΔE = Lnc ⇒ Lnc = LN
h
N
La normale è perpendicolare allo
spostamento: quindi il suo lavoro è nullo
P
ΔE = Lnc = 0 ⇒ Ei = E f
Si ritorna al caso precedente
2
0 + mgh = 12 mv f + 0
K i + Ui = K f + Uf
v f = 2gh
La velocità finale è la stessa del caso precedente Ki = 0
U i = mgh
K f = 12 mv 2f
Uf = 0
•
•
Nel terzo caso agiscono
– la forza peso, che è conservativa,
– la tensione nella corda.
Possiamo applicare la relazione lavoro energia:
h
r
dr
ΔE = Lnc ⇒ Lnc = LT
dLT = T ⋅ dr = 0
perchè T ⊥ dr
P
Il lavoro infinitesimo fatto dalla tensione
T è nullo, ma anche il lavoro complessivo
Si ritorna la caso precedente
2
0 + mgh = 12 mv f + 0
T
ΔE = Lnc = 0 ⇒ Ei = E f
K i + Ui = K f + Uf
v f = 2gh
La velocità finale è la stessa del caso precedente Ki = 0
U i = mgh
K f = 12 mv 2f
Uf = 0
•
•
Nell’ultimo caso agiscono
– la forza peso, che è conservativa,
– la reazione vincolare della guida,
• Solo la componente normale, perché per ipotesi la guida è liscia
Possiamo applicare la relazione lavoro energia:
ΔE = Lnc ⇒ Lnc = LN
dLN = N ⋅ dr = 0
perchè N ⊥ dr
N
h
r
dr
P
Il lavoro infinitesimo fatto dalla forza normale N è
nullo, ma anche il lavoro complessivo ΔE = Lnc = 0 ⇒ Ei = E f
Si ritorna la caso precedente
2
0 + mgh = 12 mv f + 0
K i + Ui = K f + Uf
v f = 2gh
Conclusione: la velocità finale è sempre la
stessa in tutti e quattro i casi esaminati.
Ki = 0
U i = mgh
K f = 12 mv 2f
Uf = 0
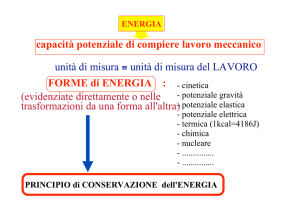
Consigli sull’uso della conservazione dell’energia nella
risoluzione dei problemi
• Separare le forze tra forze conservative e forze non conservative.
• Ricordare le forze conservative
h = quota
– Forza peso
U(x, y, z) = mgy = mgh
– Forza elastica
U(x, y,z) =
1 2
kx
2
– Forza di gravitazione universale
– Forza di Coulomb
U(x, y, z) =
U(x, y, z) = −
1 q1q 2
4πε o r
GmM
r
• Tutte le altre forze vanno considerate non conservative
• Scrivere l’equazione della conservazione dell’energia meccanica totale.
– ΔE = 0 se tutte le forze sono conservative
– ΔE = Lnc se non tutte le forze sono conservative
Problemi proposti
1) Un bambino di 75Kg scivola per un tratto di 5m su uno scivolo dritto, partendo da un’altezza di 2.5m. Determinare il
lavoro che fa la forza peso su questo bambino.
R 1840J
Problemi proposti
2) Una scatola di libri di massa 4.1Kg viene sollevata verticalmente, partendo da ferma, per un tratto di 1.6m,
applicando una forza verso l’alto pari a 60N. Determinare:
a) il lavoro fatto dalla forza applicata;
b) il lavoro fatto dalla forza peso;
c) il modulo della velocità finale della scatola.
R a) 96J, b) -64J, c) v=3.9m/s
Problemi proposti
3) Un ragazzo esercita una forza di 11N inclinata di 29° sopra l’orizzontale su una slitta di massa pari a 6.4Kg.
Determinare il lavoro fatto dal ragazzo e la velocità finale della slitta dopo che questa ha percorso 2m, sapendo
che il modulo della velocità iniziale della slitta è 0.5m/s e che questa scivola orizzontalmente senza attrito.
R v=2.5m/s
Problemi proposti
4) Quando una forza di 120N viene applicata ad una molla, ne causa l’allungamento di 2.25cm.
Qual è l’energia potenziale di questa molla, quando viene compressa di 3.5cm ?
R 3.26J
Problemi proposti
5) Un blocco di 1.70Kg scivola su una superficie orizzontale priva di attrito finché incontra una molla con una costante
elastica k=955N/m. Il blocco si ferma dopo aver compresso la molla di un tratto di 4.60cm.
Determinare il modulo della velocità iniziale del blocco.
R v=1.09m/s
Problemi proposti
6) Un maratoneta di massa 80Kg parte da fermo e corre in salita con una forte brezza, che gli soffia contro. Alla fine
della salita l’atleta ha compiuto un lavoro L1=18KJ, la resistenza dell’aria ha fatto un lavoro L2=-4420J, e il
corridore ha una velocità costante di modulo 3.50m/s.
Determinare l’altezza della collina.
R 17.3m