2) Un corpo di massa 15 kg è posto su un piano inclinato di 20°. Una forza
orizzontale di 200 N fa risalire il corpo lungo il piano inclinato con
un’accelerazione di 0.25 m/s2. Qual è il coefficiente d’attrito fra il corpo e il
piano inclinato?
3) Un corpo di 0.60 kg scivola senza attrito su un lungo piano inclinato di 30°.
Sul corpo agisce la resistenza aerodinamica R=(-0.80 kg/s) v. Calcola la velocità
limite del corpo.
Il lavoro L svolto da una forza
costante è il prodotto scalare della
forza per lo spostamento del punto
di applicazione della forza
medesima
Lavoro ed Energia
L F s Fs cos F// s
L = 0 se:
[L] = [ML2T-2]
Nxm=J
dyne x cm = erg
1J = 107 erg
F=0
s=0
= 90°
F//
(S.I.)
(C.G.S.)
esempio 1
Il lavoro svolto da F per sollevare il blocco di massa m è L = mgh
Il lavoro svolto da F durante lo spostamento d è nullo ( = 90°)
Il lavoro svolto dalla forza di gravità è Lg = -mgh
esercizio
Un uomo tira una cassa con una forza F =
90N e la sposta di 2.0 m. La fune forma un
angolo di 60° rispetto al pavimento. Calcolare
il lavoro svolto da F. Quale forza avrebbe
dovuto applicare, a parità di L, se la fune
fosse stata parallela al pavimento ( = 0°) ?
L = F x s = Fs cos = 90 J; F’ = L/(s cos ) = 45 N
θ
Lavoro svolto da una forza variabile
L j F j x
L L j F j x
F j x
x 0
L lim
x
L
f
x
i
F x dx
Lavoro svolto da una molla
F kx
x
Lel
x
f
x
i
legge di Hooke
x
f
1
Fdx kxdx kx 2
2
x
x
i
f
i
1
1
2
2
k x f xi k xi2 x 2f
2
2
Potenza
la potenza è la rapidità con cui viene svolto un lavoro
o, più in generale, la rapidità con cui viene trasferita
dell’energia
potenza
media
L
P
t
L dL
P lim
t 0 t
dt
[P] = [ML2T-3]
J/s = W
erg/s
(S.I.)
(C.G.S.)
potenza istantanea
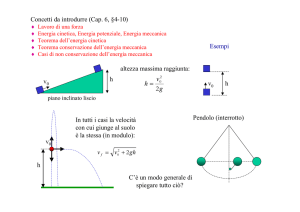
PIRAMIDE DI CHEOPE…
h=146 m;
V= 2,3 x106 m3;
2,5 x106 blocchi;
20 anni;
rroccia=2700 Kg/ m3
Energia cinetica e teorema delle forze vive
1 2
K mv
2
teorema delle forze vive
energia cinetica
L K
l’energia è la capacità di compiere un lavoro
Campi di Forza
campo: regione dello spazio sotto l’azione di una forza.
Ad ogni punto dello spazio si può associare un vettore
che rappresenta la forza agente su un corpo sonda posto
in quel punto.
esempio: campo
gravitazionale (radiale
attrattivo)
un campo viene rappresentato graficamente
mediante le linee di forza (tangenti al vettore
campo).
campo elettrico, +q
(radiale repulsivo)
Forze conservative e forze non conservative
1
B
L F ds
A
B
3
A
se L1 L2 L3 forza non conservativa
2
se L1 = L2 = L3 forza conservativa
se le forze sono conservative il lavoro lungo un
percorso chiuso è nullo
LAA = L1 + (-L2) = 0
U x, y , z
Energia Potenziale
LAB U x A , y A , z A U xB , y B , z B U A U B
U U B U A LAB
[U] =
U(x,y,z) è definita a meno di
una costante additiva
L AB U A U B
J (S.I)
erg (C.G.S)
[ML2T-2]
C
A
se UB = 0 LAB = UA
Se prendiamo C come posizione di riferimento
LAB = LAC + LCB = UA –UC + UC – UB = UA – UB
B
B posizione di riferimento
LAC = UA – UC
LCB = UC – UB
L’energia potenziale in un punto è il lavoro svolto dalle forze del campo
per spostare il corpo da quel punto alla posizione di riferimento.
esempio: il campo gravitazionale è conservativo
L AB P h mgh
A
O
d
energia potenziale
gravitazionale
c
h
P = mg
B
U L mgdy mgy
A
b
a
y
B
L AB L AC LCB
L AC P d mg d cos mg sen d mgh
LCB 0 L AB mgh
U mgh
C
esempio: il campo dovuto all’azione di una
forza elastica è conservativo
1
L k xi2 x 2f
2
F kx
se xi = xf (ciclo) L = 0 Fel è conservativa
1
U L k ( x 2f xi2 )
2
se xi = 0
1 2
U x kx
2
energia potenziale elastica
l’energia è la capacità di compiere un lavoro
Principio di conservazione dell’energia meccanica
ipotesi: campo conservativo, sistema isolato
L U i U f U
1 2 1 2
L mv f mvi K
2
2
U i U f K f Ki
Ki U i K f U f
E = energia meccanica totale
K U E
in un sistema isolato in cui agiscano solo forze
conservative l’energia meccanica totale si conserva
esempio: moto di un grave
se U(yi) = 0 e vf = 0
1 2
1 2
mvi mgyi mv f mgy f
2
2
1 2
mvi mgy f
2
vi2
yf
2g
esempio: sistema massa molla
1 2 1 2 1 2 1 2
mvi kxi mv f kx f
2
2
2
2
se U(xi) = 0 e vf = 0
1 2 1 2
mvi kx f
2
2
2
2 mvi
xf
k
Per rendere fertili le uova, lo sperma del granchio reale deve
penetrare attraverso due strati protettivi dello spessore di circa 40
mm. Per ottenere ciò un insieme lungo 60 mm di filamenti di
actina assemblati tra loro viene raddrizzato e spinge con una
forza di 1.9x10-9 N. Se i filamenti di actina hanno una massa
dell’ordine di 10-16 Kg, quale è il modulo della velocità di
filamenti alla fine di questo processo?
h=?
2
Un vagone di massa m=1000 Kg viene sparato da una molla di
costante k=1000 N/m sul punto iniziale di un percorso di
montagne russe (h=60m). Di quanto è stata accorciata la molla
durante il caricamento per raggiungere quel punto?
Una volta partito il vagone che velocità avrà nel punto 2=?
Se per attrito si perde un 30 % dell’energia nel punto 2 quanto
sarà l’altezza nel punto B?
Quantità di moto
Data una particella di massa m e velocità v si definisce
quantità di moto: p = mv [P] = [MLT-1] Kg m/s (S.I.)
Esempio: v = 10 m/s, m1 = 1 kg, m2 = 10 kg p1 = 10 kg m/s, p2 = 100 kg m/s
d v d m v d p
F ma m
dt
dt
dt
dp
Fris
Fext
dt
dp
Fris 0
0 p cos t.
dt
Relazione valida anche per sistemi a
massa variabile
II legge di Newton
Se il sistema è isolato la
risultante delle forze è nulla e
la q.m. si conserva
esempi: il cannone e il biliardo
m1, v1
m2, v2
p1i p2i p1 f p2 f
se si conserva
anche
l’energia
cinetica l’urto si
dice ELASTICO
URTI….
m1v1i m2 v2 i m1 m2 v f
m1v1i m2 v2 i m1v1 f m2 v2 f
1 2 1 2 1 2 1 2
m1v1i m2 v2 i m1v1 f m2 v2 f
2
2
2
2
Completamente
ANELASTICO: le due
masse dopo l’urto restano
attaccate
Completamente
ELASTICO: si conserva
anche l’energia cinetica
Il centro di massa
il centro di massa di un corpo o di
un insieme di corpi è quel punto
che si muove come se tutta la
massa fosse ivi concentrata e tutte
le forze esterne agissero in quel
punto
Fext Fris Macm
Esempio: i fuochi d’artificio