ENERGIA MECCANICA
CONSERVAZIONE
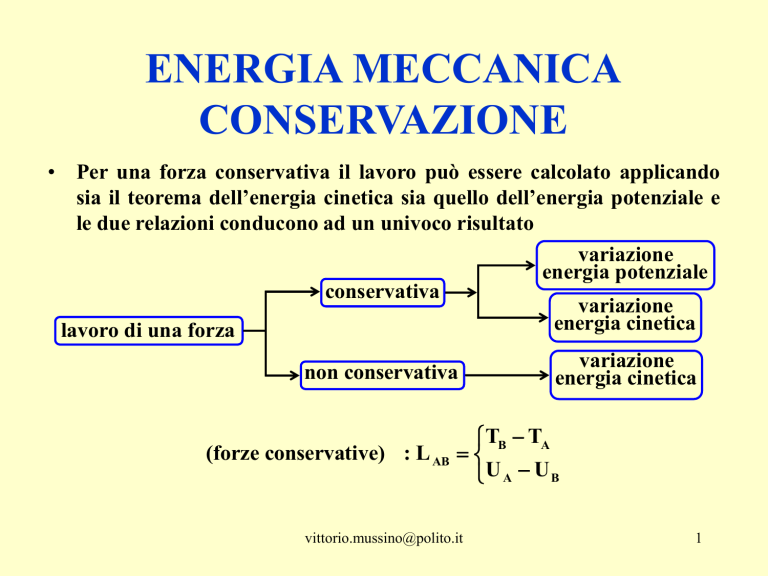
• Per una forza conservativa il lavoro può essere calcolato applicando
sia il teorema dell’energia cinetica sia quello dell’energia potenziale e
le due relazioni conducono ad un univoco risultato
variazione
energia potenziale
conservativa
variazione
energia cinetica
lavoro di una forza
non conservativa
(forze conservative) : L AB
variazione
energia cinetica
TB TA
U A UB
[email protected]
1
Uguagliando si ricava
TB TA U A U B
• La somma dell’energia cinetica e dell’energia potenziale è detta
“energia meccanica” e la relazione
TA U A TB U B
EA
EB
implica che l’energia meccanica dello stato iniziale è uguale all’energia
meccanica dello stato finale, cioè l’energia meccanica è conservata
(resta costante nel tempo) quando agiscono solamente forze di tipo
conservativo
E A EB
E cost
[email protected]
2
• Lanciando verticalmente la massa m da un’altezza h con velocità v0,
calcolare con quale velocità arriverà al suolo.
Scegliendo un
riferimento verticale, concorde con la direzione del moto e con origine
nel punto iniziale del moto, la massa cadrà sotto l’azione della sola
forza peso (trascurando la resistenza dell’aria). Essendo la forza peso
conservativa, applicando la conservazione dell’energia meccanica
E i Ef
O
Ti U i Tf U f
1
2
Ti mv 0
stato iniziale :
2
U i mgh
1
2
Tf mv
stato finale
:
2
U f 0
[email protected]
v0
h
P
v
3
Sostituendo si ricava
ossia
1
1
2
m v0 m g h m v2
2
2
v v 02 2gh
Risolvendo il problema usando le equazioni della cinematica, il moto
della massa è uniformemente accelerato con accelerazione uguale a
quella di gravità g
1 2
h v 0 t gt
2
v v 0 gt
ricavando il tempo dalla seconda equazione e sostituendolo nella
prima si ottiene proprio il precedente valore della velocità.
─ La massa sia quella di un tuffatore (m = 70 kg) che si lascia cadere
da una piattaforma alta h = 10 m rispetto all’acqua: poiché la
velocità iniziale è nulla, il tuffatore toccherà l’acqua con velocità
v 2gh 14m s
[email protected]
4
1m s 3.6km h
la velocità di impatto varrà circa 50 km/h (nella realtà, tenendo
conto delle forze di attrito circa 46 km/h). Tale valore impone al
tuffatore di presentare la minima sezione all’impatto con l’acqua
per evitare gravi lesioni agli organi interni in quanto la sua
energia cinetica (T 6860 J) deve essere dissipata nel breve
intervallo temporale dell’impatto.
ATTENZIONE: se alla massa fossero applicate forze sia conservative
sia non conservative, il teorema dell’energia cinetica enuncia che il
lavoro complessivo LAB (somma del lavoro Lc delle forze conservative e
del lavoro Lnc di quelle non conservative) è pari alla variazione
dell’energia cinetica
L AB Lc Lnc TB TA
Ricordando che il lavoro delle forze conservativa vale
Lc U A U B
si ricava
[email protected]
5
U A U B L nc TB TA
L nc TB U B TA U A E B E A E
Quando un sistema di forze qualsiasi è applicato ad una massa, il lavoro
totale delle forze non conservative è uguale alla variazione di energia
meccanica subita dalla massa.
─ Il lavoro delle forze non conservative dissipa energia, quindi ha
segno negativo Lnc < 0 per cui
L nc E B E A 0
EB E A
in un qualsiasi processo fisco reale l’energia meccanica finale è
sempre minore di quella iniziale. Questo risultato dimostra che la
conservazione dell’energia meccanica è una condizione ideale
perché si ha sempre dissipazione di energia (ricordare che il II
principio della termodinamica impone un preciso limite a quanto
si ottiene attraverso un processo fisico rispetto a quello che si è
speso affinché il processo avvenga).
[email protected]
6












