esercizio 1

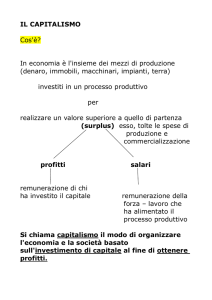
ESERCIZIO 1
Si consideri un mercato in cui opera una sola impresa caratterizzata da MC=AC=2 (costi marginali
e medi costanti). Nel mercato, la funzione di domanda è
P = 10 – 2X
a) Quale sarà la quantità prodotta dall’impresa ?
La curva dei MR, data la curva di domanda lineare, avrà espressione MR=10-4X e la regola di
massimizzazione dei profitti in caso di monopolio prevede MR=MC. Perciò otteniamo 10-4X=2,
ovvero X=2.
b) Quali il prezzo di mercato e i profitti del monopolista?
P=10-2*2=6; Profitti di monopolio: TR-TC = P*X - AC*X = 6*2 – 2*2=12-4=8.
Ipotizzate ora che un intervento dell’autorità antitrust obblighi l’impresa a scindersi in due imprese,
A e B, identiche ma totalmente autonome. Se nonostante tale intervento le imprese riuscissero
comunque a colludere, ciascuna otterrebbe profitti esattamente uguali alla metà del profitto
calcolato in b). In caso di mancato rispetto dell’accordo collusivo, A e B ottengono invece profitti
che sono riassunti nella tabella seguente:
Azioni
Profitto di A
Profitto di B
8/ 2=4
10
2
3
8/ 2=4
2
10
3
A e B colludono
A devia e B no
B devia e A no
Entrambi deviano
c) Si calcoli il profitto per ciascuna impresa in caso di collusione e si rappresenti (in forma
normale ed estesa) il gioco simultaneo delle due imprese che devono decidere se colludere o
deviare.
B
A
Coll
Dev
Coll
Dev
(4 , 4)
(2 ,10)
(10, 2)
(3,3)
1
d) Si determini l’equilibrio del gioco e lo si caratterizzi.
L’equilibrio di Nash del gioco risulta (Dev,Dev), che è anche un equilibrio in strategie dominanti.
e) L’equilibrio ottenuto in d) è Pareto-efficiente?
Tuttavia, l’equilibrio del gioco non è Pareto-efficiente, in quanto entrambi i giocatori potrebbero
migliorare la propria situazione se riuscissero a convergere sulla strategia (Coll,Coll).
2
Esercizio 2
Due imprese simmetriche operano in regime di duopolio in un mercato la cui curva inversa di
domanda è data da P = 100 – Q, dove Q = q1+ q2. Oltre a vendere lo stesso prodotto, esse sono
caratterizzate dalla stessa funzione di costo totale TCi = 10qi, con i=1,2.
a)
Quale sarà l’equilibrio (Q, q1, q2 , P, 1, 2 e =1 + 2 ) derivante da una competizione à la
Cournot, con le imprese che scelgono simultaneamente le quantità?
Essendo le imprese simmetriche, nel caso di competizione cournotiana possiamo risolvere il
problema per l’impresa 1 e poi estendere i risultati alla concorrente.
1=P* q1-TC1=(100- q1- q2)* q1-10 q1. La condizione di ottimo richiede d1/dq1= 0, cioè
(100- q1- q2)- q1-10=0, ovvero 2q1=90 - q2, da cui la funzione di reazione per l’impresa 1:
q1(q2) = 45- q2/2 (e, per simmetria, la funzione di reazione per l’impresa 2 sarà:
q2(q1) = 45- q1/2. Mettendo a sistema le due funzioni di reazione o, più semplicemente,
ponendo q1 = q2 = q in una di esse, otteniamo q=45-q/2, da cui qiCournot=30.
QCournot= q1+ q2 =30+30=60, che, inserito nella funzione di domanda, dà PCournot=10060=40.
iCournot = PCournot * qiCournot - TCi =40*30-10*30=1200-300=900 (=[40-10]*30).
Cournot=1Cournot + 2Cournot=900*2=1800.
b)
Quali saranno i cambiamenti nella suddetta combinazione di equilibrio se le imprese
competono à la Stackelberg, con l’impresa 1 leader (1 sceglie per prima) e l’impresa 2
follower?
Il problema per l’impresa 1 diviene il seguente: max 1 s.v. q2(q1).
Dobbiamo quindi inserire nell’espressione dei profitti dell’impresa 1la funzione di reazione
dell’impresa 2, dato che il leader conosce la funzione di reazione del follower.
1=(100- q1- 45 + q1/2)* q1-10 q1=(55-q1/2)* q1-10 q1. La condizione di ottimo prevede
d1/dq1= 0, cioè 55-q1/2- q1/2-10=0, da cui q1S=45.
Sostituendo questo valore nella funzione di reazione del follower, otteniamo q2 S (q1 S) = 4545/2 = 45/2 = 22,5.
Q S = q1 S + q2 S = 45+22,5=67,5(> QCournot=60), valore che, inserito nella funzione di
domanda, fornisce il prezzo di mercato P S=100-67,5=32,5 (< PCournot=40).
I profitti delle due imprese risultano quindi: 1S=(32,5-10)*45=1012,5=profitto
leader>1Cournot>2S=(32,5-10)*22,5=506,25=profitto follower <2Cournot.
I profitti aggregati S=1S + 2S=1012,5+506,25=1518,75<1800=Cournot (aumenta surplus
consumatore a scapito dei profitti di duopolio).
3
ESERCIZIO 3
(Prova Generale di Economia Politica II del 30 Gennaio 2002 – Esercizio 2)
In un mercato caratterizzato dalla seguente domanda P = 140 – Q, due imprese con costi fissi nulli e costo marginale
MC=20 competono à la Cournot.
a)
Si calcolino prezzo, quantità e profitti d’equilibrio.
Essendo Q= q1+q2 , la funzione di domanda residuale sarà P = 140 - q1 - q2 , da cui ricavo MR1 semplicemente
mantenendo stessa intercetta verticale e raddoppiando il coefficiente angolare (funzione di domanda lineare). Quindi,
la condizione di ottimo per la singola impresa (MR i=MC), è garantita dall’uguaglianza MR1=140-2 q1 - q2 = 20 = MC
(=AC). Risolvendo per q1, otteniamo la funzione reazione per l’impresa 1: q 1= 60 – q2 / 2.
Essendo le imprese simmetriche (q1=q2), non solo la funzione di reazione per l’impresa 2 sarà uguale a quella
dell’impresa 1 ad indici invertiti ( q2= 60 – q1 / 2), ma posso facilmente ricavare da una delle due funzioni di reazione
la quantità di equilibrio q1Cournot= q2Cournot = 40.
Sostituendo nella funzione di domanda Q = q 1 Cournot +q2 Cournot =80, ottengo il prezzo d’equilibrio, PCournot=140 – 80
=60.
I profitti saranno π1Cournot= π1Cournot= (P-AC)*qi=(60-20)*40=1600.
b)
Si calcolino prezzo, quantità e profitti d’equilibrio, nel caso in cui colludano.
In caso di collusione, le imprese massimizzano i profitti congiunti. Essendo i costi marginali uguali
per le due imprese e costanti, è possibile ottenere la soluzione semplicemente applicando la regola
di massimizzazione dei profitti di un monopolista che produce quantità Q, ovvero MR=MC.
In questo caso, sempre per le note proprietà della funzione di domanda lineare, abbiamo MR=140-2Q=20=MC, da cui
QMonopolio=60.
Le due imprese si dividono equamente a metà la produzione, per cui q 1Monopolio= q2Monopolio= QMonopolio/2 = 60/2=30.
Il prezzo d’equilibrio, PMonopolio=140 – 60 =80.
I profitti saranno π1Monopolio= π1Monopoliot= (P-AC)*qi=(80-20)*30=1800.
c)
Ipotizzando che la deviazione dalla collusione permetta al traditore di ottenere tutti i profitti ma annulli quelli
del concorrente, si rappresenti il gioco in forma normale e si indichino gli equilibri di Nash.
Essendo i profitti totali di monopolio, ottenuti dall’agente traditore, pari al doppio dei profitti di
collusione (che erano proprio i profitti di monopolio divise tra le due imprese), il gioco in forma
normale avrà la seguente forma:
4
II
Colludere
Deviare
I
Colludere
Deviare
(1800,1800)
(3600,0)
L’unico equilibrio di Nash è (Deviare,Deviare), a cui sono associati i pay-offs (1600,1600).
5
(0,3600)
(1600,1600)
Esercizio 4
(Prova Generale di Economia Politica II del 4 Novembre 2002 – Parte III)
Due imprese vendono un identico prodotto la cui funzione inversa di domanda è:
P = 25 – (1/4) Q
Le funzioni di costo totale delle imprese sono rispettivamente:
TC1=2Q1
TC2=(1/2)Q2
a)
Si calcolino le rispettive quantità di equilibrio, il prezzo di mercato ed i profitti nel caso
in cui le due imprese competano alla Cournot;
Essendo Q=Q1+Q2, le due funzioni di domanda residuali risultano essere:
per l’impresa 1 → P = (25-1/4 Q2) - 1/4 Q1;
per l’impresa 2 → P = (25-1/4 Q1) - 1/4 Q2;
dove i termini tra parentesi indicano le intercette verticali, mentre il coefficiente angolare resta
uguale a quello della funzione di domanda generale e pari ad ¼.
Calcoliamo la funzione di reazione per l’impresa 1 ponendo MR1=MC1. Anche senza passare
tramite il calcolo dei ricavi totali, posso scrivere MR1 utilizzando la regola valida per le
funzioni di domanda lineare: MR1=(25-1/4 Q2) - 1/2 Q1 [stessa intercetta verticale e pendenza
doppia].
MC1=2=(25-1/4 Q2) - 1/2 Q1 =MR1, da cui ricavo R1: Q1(Q2)=46-1/2Q2.
Procedendo in modo analogo nel calcolo della funzione di reazione per l’impresa 2, ottengo:
MC2=1/2=(25-1/4 Q1) - 1/2 Q2 =MR2, da cui ricavo R2: Q2(Q1)=49-1/2Q1.
Ponendo in sistema R1 con R2, ottengo le quantità di equilibrio pari a Q1* = 86/3 (~28,6) e a
Q2* = 104/3(~34,6).
P* =25-1/4(104/3+86/3)=25-95/6=55/6.
π1=(55/6)*(86/3) – 2*(86/3) = (2365-516)/9 = 1849/9.
π2=(55/6)*(104/3) –1/ 2*(104/3) = (2860-156)/9 = 2704/9.
6
La rappresentazione grafica della situazione di equilibrio è:
Q2
92
R1
49
E
104/3
R2
86/3
b)
46
98
Q1
Si calcolino i precedenti valori nel caso si comportino come due oligopolisti alla
Bertrand;
Essendo MC1=2 e MC2=1/2, l’impresa 2 avrà convenienza a fissare un prezzo 2-, insostenibile
per l’impresa 1, servendo tutta la domanda per quel prezzo, cioè Q=Q2, che trovo risolvendo la
funzione di domanda per P=2- : 2- =25 -1/4Q, da cui, tracurando, Q=92.
I profitti delle due imprese saranno quindi π1=0 e π2=2*92-1/2*92=184-46=138.
c)
Quale tipo di competizione preferirebbero le due imprese, se potessero scegliere?
Potendo scegliere, le imprese preferiranno entrambe la competizione alla Cournot, essendo:
π1Cournot=1849/9> π1Bertrand=0 e π2Cournot=2704/9~300 > π2Bertrand=138.
7