DERIVATA
Sia y = f(x) una funzione reale definita in un intorno di x0.
Si consideri un incremento (positivo o negativo) di x0: ∆x = h; la funzione
passerà allora dal valore f(x0) a quello di f(x0+h), subendo così un incremento
∆y = f(x0+h) - f(x0). Si definisce rapporto incrementale della funzione f(x0) il
rapporto tra l'incremento della funzione e l' incremento corrispondente della
variabile indipendente, cioè:
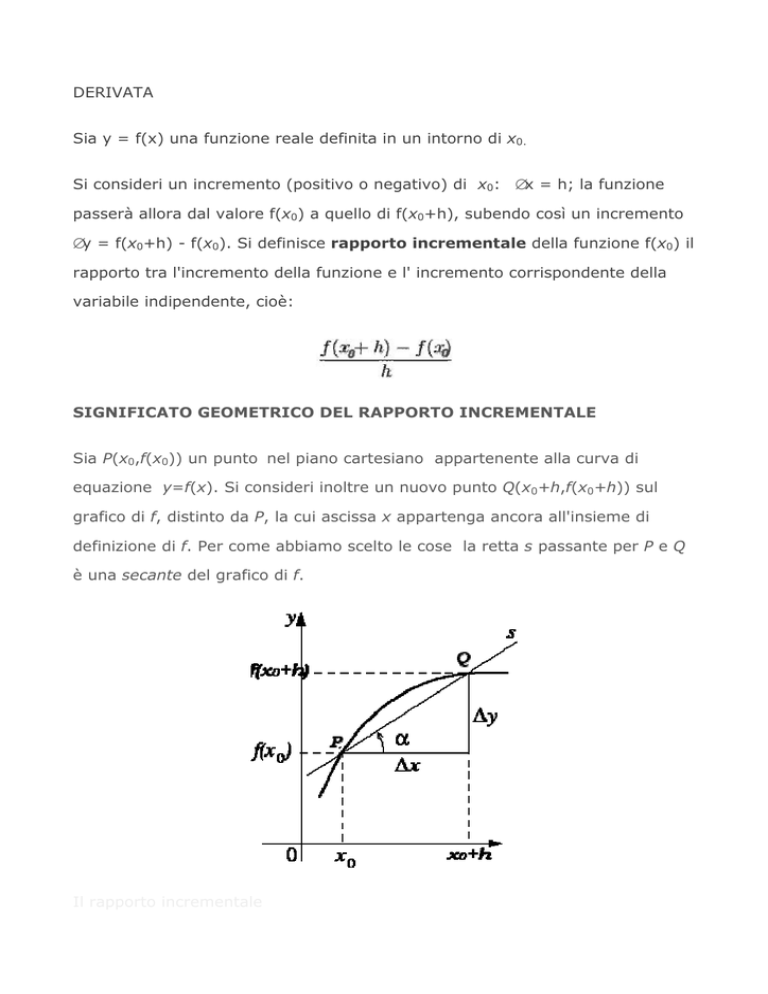
SIGNIFICATO GEOMETRICO DEL RAPPORTO INCREMENTALE
Sia P(x0,f(x0)) un punto nel piano cartesiano appartenente alla curva di
equazione y=f(x). Si consideri inoltre un nuovo punto Q(x0+h,f(x0+h)) sul
grafico di f, distinto da P, la cui ascissa x appartenga ancora all'insieme di
definizione di f. Per come abbiamo scelto le cose la retta s passante per P e Q
è una secante del grafico di f.
Il rapporto incrementale
è il coefficiente angolare della retta PQ, cioè il valore della tangente
dell’angolo che la retta PQ forma con l’asse delle x (per il secondo teorema sui
triangoli rettangoli).
DERIVATA DI UNA FUNZIONE IN UN PUNTO X0
DEFINIZIONE
La derivata di una funzione rappresenta la variazione che subisce la funzione f
rispetto alla variabile x.
Si definisce derivata della funzione reale y = f(x) in un punto x0 (e si indica
con f'(x0) ), il limite, se esiste ed è finito , del rapporto incrementale:
cioè
Si parlerà di derivata destra (sinistra) se esiste ed è finito il limite destro
(sinistro)del rapporto incrementale.
Una funzione è derivabile in un punto x0 se la derivata destra coincide con la
derivata sinistra.
SIGNIFICATO GEOMETRICO DELLA DERIVATA
Quando h tende a zero, il punto P si avvicina sempre più al punto Q: la retta
PQ allora, che dapprima era secante la curva, non diventa altro che la retta
tangente alla curva nel punto x0 e l'angolo α tende all'angolo β.
Perciò la f’(x0) non rappresenta altro che il coefficiente angolare della retta
tangente alla curva nel punto x0 .
Applicazioni delle Derivate
1) Equazione della tangente a una curva in un punto:
Consideriamo una curva generica y=f(x). La retta tangente alla curva in un punto P0 di ascissa x0 ha
come coefficiente angolare m la derivata della funzione
calcolata nello stesso punto di ascissa x0, ossia f’(x0)
[significato geometrico della derivata] [Fig. 2].
Quindi possiamo scrivere:
m = f ' ( x0 )
L’equazione della tangente a una curva y=f(x) in un punto P0(x0,y0), è data dalla formula [ottenuta
sostituendo al posto di m, f’(x0)]:
y − y0 = f ' ( x0 ) ⋅ ( x − x0 )
Uso dei limiti per il calcolo delle derivate
PREMESSA : Teorema del Confronto
Siano
tre funzioni definite su un dominio X di
. Se
ed esiste un intorno U di x0 tale che
allora
ESEMPIO 1.
Sfruttando il fatto che per
Per i reciproci vale:
ora si moltiplica per sin x:
vale
Ma cos x tende all'unità per x che tende a zero, quindi per il teorema del confronto il limite in
mezzo dovrà avere lo stesso valore degli altri due
Esempio 2.
•
Moltiplicando il denominatore e il numeratore per 1 + cos(x) abbiamo che:
Ma poiché sin2(x) = 1 − cos2(x):
Quindi
Moltiplicando il denominatore e il numeratore per 1 + cos(x) abbiamo che:
Ma poiché sin2(x) = 1 − cos2(x):
Quindi
Applichiamo i limiti notevoli per calcolare la derivata di y = sen x
f(x) = sen x
f(x+h) = sen (x+h)
faccio il limite del rapporto incrementale:
sen (x+h) - sen x
limh->0 ------------- ---------=
h
applico la regola della somma per sen (x+h)
sen x cos h + cos x sen h
Per il teorema sulla somma dei limiti
=limh->0 (sen x cos h - sen x) / h + limh->0 cos x sen h/ h=
=limh->0 sen x (cos h - 1) / h + limh->0 cos x ·(sen h/ h)=
=(sen x)· limh->0 (cos h - 1) / h + (cos x) ·limh->0 sen h/ h=
= limh->0 (sen x)·(1/2)h + (cos x) ·1 = cos x
quindi la derivata di y = sen x e' y' = cos x
La derivata di y = x2
f(x) = x2
f(x+h) = (x+h)2
faccio il limite del rapporto incrementale:
(x+h)2-x2
limh->0 --------------- =
h
sviluppo il quadrato
x2+2hx+h2-x2
=limh->0 ------------ -------=
h
=limh->0 (2hx+h2) / h=
Per il teorema sulla somma dei limiti
=limh->0 2hx / h + limh->0 h2 / h=
=limh->0 2x + limh->0 h = 2x
Regole di derivazione:
Per la derivata di una funzione somma di più funzioni derivabili vale il seguente teorema:
La derivata della somma di due (o più) funzioni derivabili, esiste ed è uguale alla somma delle
derivate delle singole funzioni.
Se è:
y=f+g
con f e g funzioni derivabili in x, sarà per il teorema enunciato:
y’ = f’ + g’.
Per la derivata di una funzione prodotto di due funzioni derivabili vale, invece, il seguente
teorema:
La derivata del prodotto di due funzioni derivabili, esiste ed è uguale al prodotto della derivata del
primo fattore per il secondo, più il prodotto del primo fattore per la derivata del secondo.
Se è:
y = f⋅g
con f e g funzioni derivabili in x, sarà per il teorema enunciato:
y’ = f’⋅g + f⋅g’.
Per la derivata di una funzione quoziente di due funzioni derivabili vale, infine, il seguente
teorema:
La derivata del quoziente di due funzioni derivabili, esiste ed è uguale a una frazione avente al
denominatore il quadrato del denominatore e al numeratore la differenza tra il prodotto del denominatore
per la derivata del numeratore e il prodotto del numeratore per la derivata del denominatore.
Se è:
f
y = --g
con f e g funzioni derivabili in x, sarà per il teorema enunciato:
f’⋅g - f⋅g’
y’= -------------g2
Tabella di derivate
Per semplificare il calcolo della derivata di una funzione, è stata predisposta una tabella di facile
consultazione. Si riporta a sinistra la funzione y=f(x) e, a destra, la derivata y’=f’(x) in un generico
punto, dove la funzione è derivabile:
y=f(x)
y’=f’(x)
y=k
y '= 0
Funzione potenza:
y ' = αxα −1
y = xα
In particolare:
y=x
y= x
y' = 1
y' = sgn x =
x − 1 se x < 0
quindi in x=0 non
x + 1 se x > 0
è derivabile(derivata destra diversa dalla
derivata sinistra)
y=n x
y=
y=
y' =
1
x
1
n n x n −1
y' = −
x
y '=
1
x2
1
2 x
Funzioni trigonometriche:
y = sen x
y ' = cos x
y = cos x
y ' = − sen x
y = tgx
y = ctgx
y' =
y' = −
1
= 1 + tg 2 x
2
cos x
1
= −(1 + ctg 2 x)
sen 2 x
Funzione logaritmica:
y = log a x
y' =
1
1
log a e =
x
x ln a
In particolare:
y = ln x
y' =
1
x
Funzione esponenziale:
y = ax
y ' = a x ln a
Principali regole di derivazione:
y = k ⋅ f (x)
(k = costante)
y ' = k ⋅ f ' ( x)
y = f ( x) + g ( x)
y ' = f ' ( x) + g ' ( x)
y = f ( x) ⋅ g ( x)
y ' = f ' ( x ) ⋅ g ( x ) + f ( x ) ⋅ g ' ( x)
y=
f ( x)
g ( x)
y' =
f ' ( x) ⋅ g ( x) − f ( x) ⋅ g ' ( x)
[ g ( x)]2
Esempio : Calcolare l’equazione della retta tangente alla curva f(x) = √2 cos(x/4) nel punto
corrispondente a x = π
f ’(x)= −
2
x
2 1
1
×
=−
sen , m = f ' (π) = 4
4
4
4
2
f(π) = 1, quindi
1
y = − ( x − π) + 1
4
LIMITI DI FORME INDETERMINATE-Teorema di De L’Hospital
La conoscenza delle derivate e delle principali regole di derivazione è utile, fra l’altro, per il calcolo
di certi limiti che si presentano sotto forma indeterminata quali il quoziente di due funzioni che tendono
simultaneamente a zero
0
0
o all’infinito
∞
∞
A tale scopo, lo strumento fondamentale è fornito dal seguente teorema:
Siano f(x) e g(x) due funzioni derivabili in un’intorno H del punto c (escluso eventualmente c),
con g’(x)≠0.
Se è:
lim f ( x ) = lim g( x ) = 0,
x →c
x →c
oppure f e g continue con
oppure
lim f ( x ) = lim g (c) = ∞.
x →c
Se esiste il
lim
x→ c
x →c
f ' ( x)
f ( x)
, allora esiste anche il lim
, e si ha:
x→ c g ( x )
g ' ( x)
lim
x →c
f ( x)
f ' ( x)
= lim
.
x
→
c
g ( x)
g ' ( x)
f (c) = g (c) = 0,
Se il quoziente
∞
,
∞
f ' ( x)
nel
g ' ( x)
punto x=c presenta di nuovo una indeterminazione del tipo
0
,
0
o
e se le funzioni soddisfano le condizioni del teorema, conviene allora passare alle derivate
seconde, ecc.
Esempio:
Supponiamo di voler calcolare il valore del limite della seguente funzione:
x2 + 5x − 6
.
x →1 x 2 + x − 2
lim
Se sostituissi al posto della x il valore a cui essa tende, ossia 1, otterrei:
x2 + 5x − 6 (1)2 + 5(1) − 6 0
=
=
x →1 x 2 + x − 2
(1)2 + (1) − 2 0
lim
L’espressione
0
, come è noto, è una forma indeterminata.
0
Applichiamo il teorema di De L’Hospital. Derivando numeratore e denominatore si ha:
x 2 + 5x − 6
2x + 5
= lim
2
x →1 x + x − 2
x →1 2 x + 1
lim
Se provo a rifare la sostituzione, stavolta, ottengo:
2 x + 5 2(1) + 5 7
=
=
x →1 2 x + 1
2(1) + 1 3
lim










