IL V POSTULATO
Verso la fine del IV secolo a.C. Euclide cercò di dare un assetto rigoroso alla geometria a partire
da verità evidenti e da postulati che garantiscono l'esistenza di oggetti effettivamente costruibili
con riga e compasso.
Mentre però per i primi 4 postulati è facile individuare il carattere di costruttività, per l’ultimo, il
quinto questo aspetto non è così evidente.
Il I postulato infatti garantisce la possibilità di condurre una retta (concepita come segmento)
passante per due punti dati; con il II è possibile prolungare una retta (segmento) indefinitamente;
il III ci permette di costruire (con un compasso ideale!) circonferenze di raggio qualunque; il IV
è necessario per garantire che l'angolo retto ottenuto costruendo due rette che incontrandosi
formano angoli adiacenti uguali, non dipende dalle rette considerate Il V infine, e qui siamo al
punto cruciale, garantisce sì l'esistenza del punto di intersezione tra due rette che formano con
una trasversale angoli coniugati minori di due retti, ma non dà alcuna indicazione su come si.
possa costruirlo.
Ad Euclide era già chiara la differenza sostanziale tra i primi 4 postulati e l'ultimo, e fece lo
sforzo di dimostrare il maggior numero di teoremi evitando di ricorrere al V.
Per esempio uno dei primi teoremi afferma
“In un triangolo angolo esterno è maggiore di ciascun angolo interno non adiacente.”
Ed un altro
" in ogni triangolo la somma di due angoli, comunque presi,è minore di due retti",
1
Entrambi potevano essere dedotti da teoremi successivi
( “in un triangolo un angolo esterno è uguale alla somma degli angoli interni non adiacenti”
. " in ogni triangolo la somma degli angoli interni è uguale a due retti",
E' evidente come Euclide intendesse mostrare fino a che punto si poteva giungere senza fare
ricorso al V postulato.
In effetti introduce il V postulato prima della proposizione 29
Possiamo dire quindi che lo stesso Euclide, con le prime 28 proposizioni , costruì una specie di
geometria non euclidea, nel senso che non si tratta di una geometria che nega il V postulato ma
di una "geometria assoluta" o neutrale , che ne prescinde.
LA TEORIA DELLE PARALLELE
Ricordiamo una nota proprietà della Geometria Euclidea:
Condizione necessaria e sufficiente affinché due rette siano parallele è che, tagliate da una
trasversale formino
Angoli corrispondenti uguali
Angoli alterni uguali
Angoli coniugati supplementari
Le tre proprietà sono dipendenti l’una dall’altra, pertanto possiamo concentrare la nostra
attenzione su una sola di esse, per esempio sulla proprietà che gli angoli coniugati interni ( che
indicheremo con α e β rispettivamente) siano supplementari.
Proviamo a seguire sinteticamente l’itinerario di Euclide :
Senza usare il V postulato , Euclide dimostra la proposizione seguente( proposizione17)
a) Se due rette si incontrano ,formano con una trasversale angoli α e β tali che α + β <π
da cui si deduce per assurdo
b) Se due rette formano con una trasversale angoli α e β tali che α + β =π,
allora sono parallele (proposizione 28: criterio di parallelismo)
β
β
α
α
α + β <π
α + β =π,
Non riesce però a dimostrare la proposizione inversa della b) (proposizione 29)
( se due rette sono parallele allora α + β =π) ,
β
2
α
α + β =π ?
se non introducendo come postulato la proposizione inversa della a)
Se una retta venendo a cadere su due rette forma gli angoli interni e dalla stessa parte minori di
due retti, le due rette prolungate illimitatamente verranno ad incontrarsi da quella parte in cui
sono gli angoli minori di due retti, il famoso V postulato
Il quinto postulato di Euclide è stato oggetto di molte dispute.
Per diversi secoli i matematici coltivarono la convinzione che questo postulato dipendesse dagli
altri quattro che lo precedono e che pertanto si potesse dimostrare come un teorema. Molti
matematici si cimentarono dunque nella dimostrazione del V postulato senza avere, però, grandi
successi. Nella maggioranza dei casi la dimostrazione si basava su ipotesi che andavano
semplicemente a sostituirlo senza avere peraltro un maggior carattere di evidenza e di
costruttività.
John Playfair (1748-1819) elaborò quella che forse è la versione più conosciuta del quinto
Postulato:
Data una retta ed un punto non appartenente ad essa, esiste ed è unica una retta passante per il
punto e parallela alla retta data
E’ facile verificare che le due formulazioni sono l’una conseguenza dell’altra, quindi
logicamente equivalenti.( Basta osservare che dal V postulato Euclide deduce la proposizione 29
e poi la proposizione 30: due rette parallele ad una terza sono parallele tra di loro, da cui l’unicità
della parallela ad una retta data per un punto assegnato).
Tra il 1829 e il 1830 un matematico russo Nikolay Lobacevskij, ricordato come il Copernico
della Geometria, ebbe il coraggio di affrontare il problema su strada opposta: propose una
geometria nella quale fosse contemplata, in sostituzione del quinto postulato di Euclide, una
diversa asserzione sul parallelismo tra rette. Nel 1829-30 pubblicò sul "Messaggero di Kazan" un
lavoro nel quale viene esposta la nuova geometria, da lui chiamata "Geometria immaginaria",
sviluppata sino alla trigonometria ed al calcolo di aree e volumi. Con tale articolo egli era il
primo matematico a fare il passo rivoluzionario consistente nel pubblicare una nuova geometria
(con termine moderno denominata iperbolica) costruita su un'ipotesi che era in diretta
contraddizione con il V, la negazione dell' unicità della parallela: per un punto C che giace al di
fuori della retta r si può tracciare nello stesso piano più di una parallela ad r. Da questo postulato
deduceva una nuova struttura geometrica che non presentava nessuna contraddizione logica
interna
Anche l’ungherese Janos Bolyai, tra il 1820 e il 1823, in età molto giovane, essendo nato nel
1802, scrisse un trattato su un sistema di Geometria non Euclidea.
Prima di pubblicare il suo lavoro, purtroppo scoprì che Gauss aveva già introdotto gran parte dei
suoi risultati. Sebbene Gauss non pubblicò niente a riguardo, questa scoperta per il giovane
Bolyai fu un vero colpo, tanto che abbandonò le sue ricerche. Comunque il suo lavoro fu
pubblicato nel 1832 come un'appendice di un trattato di suo padre Farkas.
E’ interessante osservare che Janos si era dedicato alla teoria delle parallele nonostante
l’esplicito scoraggiamento da parte del padre: “…per amor del cielo ti imploro di desistere dal
tentativo. Il problema delle parallele è una cosa da temere e da evitare non meno delle passioni
dei sensi, poiché anch’esso può rubarti tutto il tuo tempo e privarti della salute, della serenità e
3
della felicità che Janos aveva comunicato l’entusiasmo per la sua scoperta con parole molto
suggestive: “ Ho fatto scoperte così meravigliose che ne sono rimasto quasi abbagliato.
Dal nulla ho creato un mondo nuovo..”)
Nel 1854 Riemann introduce la Geometria ellittica, che sostituisce al V postulato
negazione dell’esistenza di una parallela ad una retta data per un punto esterno.
con la
La negazione del V postulato fa cadere uno dei più noti teoremi della geometria euclidea, il
teorema che afferma che la somma degli angoli interni di un triangolo è sempre uguale ad un
angolo piatto.
Nella geometria iperbolica tale somma è sempre minore di un angolo piatto, nella geometria
ellittica maggiore.
Introduzione alle geometrie non euclidee
Uno dei postulati logicamente equivalenti al V è quello di Playfair,:
Data una retta r ed un punto p fuori di esso, esiste una e una sola parallela ad r passante per P.
Se proviamo a negare questa affermazione possiamo fare due ipotesi
1. Non esistono rette parallele ad r
2. Esistono almeno due rette parallele ad r
Cercando di non lasciarci condizionare dalle proprietà che siamo abituati ad attribuire alle rette
secondo il modello euclideo, ragioniamo in questo modo
P
s
r
H
Q
Da P tracciamo la perpendicolare PH ad r e poi un’altra retta che incontri in Q la retta r.
Al variare di s nel fascio di centro P si possono avere due eventualità
a) Q ritornerà nel punto di partenza H
b) Q non ritornerà mai nel punto di partenza
Nel primo caso il V postulato viene sostituito dalla proposizione
Data una retta r ed un punto p fuori di esso, non esiste alcuna parallela ad r passante per P.
Si costruisce così la Geometria Ellittica
In questa Geometria viene negato anche il postulato dell’infinità della retta.
4
Nel secondo caso esisteranno
Rette secanti r
Rette non secanti r
Le rette limite, che separano le secanti dalle non secanti, saranno dette parallele ad r.
Il V postulato sarà pertanto sostituito dall’affermazione:
Data una retta r ed un punto p fuori di esso, esistono due parallele ad r passanti per P.
Si costruisce così la la Geometria Iperbolica.
Vediamo meglio come è possibile pensare che vi siano due parallele alla stessa retta passanti per
lo stesso punto.
Siamo abituati a pensare che, data AB ed il punto P, ci sia solo la retta CD come parallela alla
prima.
fig.1
Ma proviamo a pensare che ne esista una seconda: pensiamo ad una retta passante per P che non
coincida con CD.
fig.2
Diremmo che questa non possa essere parallela ad AB perché convinti che incontri AB in un
certo punto prima o poi. Ma proviamo a prescindere dall'apparenza del disegno; possiamo
dimostrare che
il prolungamento di EF debba per forza incontrare AB?
Teniamo presente che siamo in una geometria neutrale a cui abbiamo aggiunto la negazione del
postulato di Playfair, non abbiamo più il teorema 30 di Euclide che ci dice che rette parallele ad
una stessa retta sono parallele fra loro, quindi non deve disturbarci il fatto che nel nostro caso EF
e CD, entrambe parallele ad AB, si incontrino in P.
5
E ancora, non abbiamo più il postulato di Euclide che ci porterebbe a dire che,
poiché PQB+QPF<180°, le due rette AB e EF si incontrano.
fig.3
E potremmo andare avanti ancora, scontrandoci con asserzioni logicamente equivalenti al V
postulato, e trovandoci a dover ogni volta ricordare che l'abbiamo negato.
Per verificare la coerenza della Geometria ellittica e della Geometria iperbolica dobbiamo
costruire alcuni Modelli, assegnando agli enti primitivi un preciso significato fisico, o quanto
meno suscettibile di rappresentazione come le <<figure >> della geometria euclidea..
Basterà costruire <<modelli euclidei>> delle geometrie non euclidee perché la coerenza di
queste ultime sia una conseguenza della coerenza della geometria euclidea.
Questa affermazione sarà più chiara dopo aver familiarizzato con i modelli .
Il modello di Klein e il modello di Poincaré della geometria iperbolica
Il modello di Klein è tra i più semplici della geometria iperbolica. Si tratta di un modello di
questa geometria in cui i concetti di punto, retta, piano, non hanno una rappresentazione granché
diversa rispetto a quanto siamo abituati nella geometria di Euclide. La cosa radicalmente diversa
è costituita dal fatto che non vale il postulato delle parallele nella forma di Euclide.
Consideriamo un cerchio, che indichiamo con C, e diamo le seguenti definizioni:
Punto è un punto interno (sono cioè esclusi i punti sul bordo).
Retta è una qualunque corda, privata degli estremi.
Piano è l'insieme di tutti i punti interni.
Naturalmente è necessario introdurre un nuovo concetto di congruenza e e un nuovo modo
di calcolare la distanza tra due punti
Si introduce quindi questa corrispondenza
Piano
Punto
Retta
Gruppo dei movimenti rigidi
Insieme dei punti interni a C
Punto interno a C
Corda privata degli estremi
Gruppo delle omografie che mutano in sé la
6
Segmenti congruenti
Distanza Euclidea
regione interna a C
Segmenti che si corrispondono in un’omografia
Distanza iperbolica
Le omografie sono particolari trasformazioni proiettive, trasformazioni più generali delle
affinità, che conservano il birapporto di 4 punti allineati .
Il birapporto di 4 punti allineati (A,B,C,D) è dato dal rapporto dei due rapporti semplici
( ABC ) AC BD
( ABD ) BC AD
Ricordiamo come si calcola la distanza euclidea tra due punti A e B
( xA xB )2 ( y A yB ) )2
ovvero
( xB xA )
quando si consideri la distanza orientata su una retta ( parallela all’asse x)
Per la distanza iperbolica si procede così:
considerato il segmento AB, lo si prolunga (in una retta) fino ad incontrare in M ed N la
circonferenza limite del nostro piano di Klein. Si pone poi .
che non è altro che il logaritmo del birapporto ( ABNM) ( Osservazione :l’argomento del
logaritmo è sicuramente positivo, per qualunque posizione di A e di B
Infatti
Essendo A e B punti interni al segmento MN, le distanze orientate BM e AM sono sempre
entrambe negative e le distanze orientate AN e BN sono sempre positive entrambe)
Il valore della distanza può essere però sia positivo che negativo, a seconda della
posizione dei due punti.
Qualora si volesse definire una distanza non orientata, basta introdurre nell’espressione un
valore assoluto..
Vedremo più avanti che questa scelta permette delle analogie tra le due definizioni.
Si può verificare che, in questo modello, sono validi i primi quattro postulati della ordinaria
geometria di Euclide.
7
Però se si considera una retta r ed un punto P fuori di essa, per P passano infinite rette che non
intersecano r. Nella figura sono tracciate le due rette "limite", PA e PB che non intersecano r,
perché i punti A e B della circonferenza non fanno parte del nostro "piano", ed un altra retta
intermedia, anch'essa senza intersezioni con r. Le rette PA e PB sono considerate parallele ad r,
mentre le altre sono considerate "non secanti" o "ultraparallele" (è più che altro una questione di
definizioni: nel senso usuale potrebbero tranquillamente essere definite parallele).
Una geometria come questa è stata definita iperbolica da F.Klein perché in greco iperbole
significa eccesso, in relazione al fatto che il numero di parallele è in eccesso rispetto a quanto
previsto dalla geometria di Euclide.
Nelle figure che seguono proponiamo alcune costruzioni, realizzate con Cabri
Due triangoli simmetrici rispetto ad una retta
.
AB.
8
Due cerchi di centri A e B rispettivamente
9
Un triangolo, gli assi dei tre lati e il cerchio circoscritto (L, M, N sono i punti medi dei tre lati).
Un angolo, la sua bisettrice e la sua misura.
10
Un triangolo, la misura dei suoi angoli, e la
loro somma (minore di 180° come deve
essere in questa geometria).
Un ottagono regolare e il cerchio ad esso circoscritto.
11
LA DISTANZA IPERBOLICA
Riprendiamo la formula della distanza
e facciamo alcune osservazioni, dimostrando alcune proprietà analoghe a quelle della distanza
euclidea
a)dist (AB)> 0 ↔ A è più vicino ad M e B è è più vicino ad N
Infatti da quest’ultima prpoprietà segue che, detto K l’argomento del logaritmo ,
K >1 e quindi log(K) > 0
b)Scambiando tra loro A e B , K si trasforma in 1/K , pertanto , essendo
log (1/K ) = log(1) – log(K) = -log(K)
Si ha
dist(BA) = -dist (AB)
( proprietà di simmetria)
c) dist (AB) =0 ↔ A≡B
Infatti
Se A≡B dist (AB) = log (1)=0 ( legge di annullamento)
Viceversa
Se dist (AB) = 0→
BM AN BM AN
BM
AM
1
AM BN
BN AM
BN
AN
Ma l’ultima uguaglianza può essere così interpretata:
Il punto B e il punto A dividono il segmento MN nello stesso rapporto
Pertanto A≡B
d) Se C è un punto interno ad AB
dist(AB) = dist(AC) + dist (CB) ( proprietà di additività)
12
Infatti
log
log
CM AN
log( CM ) log( AN ) log( AM ) log( CN )
AM CN
BM CN
log( BM ) log( CN ) log( CM ) log( BN )
CM BN
Da cui, sommando membro a membro)
Dist(AC)+ dist (CB) = log ( AN) + log(BM) – log (AM) – log (BN) =
BM AN
dist ( AB)
AM BN
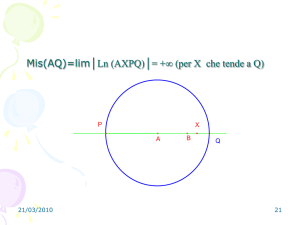
e) Se A tende ad M ( o B tende ad N) la distanza tende a + ∞
log
Infatti in ciascuno dei due casi l’argomento del logaritmo tende a +∞
ESEMPI
Scegliamo come circonferenza C di Klein, la circonferenza con centro nell’origine e raggio 4.
Siano A ,B,C,D quattro punti interni, di coordinate
A(0;0) B(1;0) C(2;0) D(3;0)
I punti M ed N avranno coordinate
M(-4;0) N(4;0)
Nella metrica euclidea le due distanze
AB eCD
Sono entrambe uguali ad 1
Applicando la formula della distanza iperbolica risulterà invece
Dist(AB) =
log
5 4
5
log
4 3
3
Dist(CD)=
7 2
7
log
log
6 1
3
Si riconosce che
Dist (AB) < dist(CD)
Si può verificare che invece il punto che ha da C distanza uguale a dist(AB) è D’(8/3;0),
ovvero un punto che da C ha una distanza euclidea di valore minore di 1
13
In altro modello della Geometria di Lobacewskij è quello di Poincaré.
Il modello di Poincaré è costruito pensando:
i punti come i punti interni ad una circonferenza C
le rette sono gli archi di circonferenza perpendicolari nei loro estremi alla circonferenza
C (nei punti di intersezione le tangenti alle due circonferenze, la C e quella cui appartiene
l'arco, sono fra loro perpendicolari) , oppure sono diametri
il piano formato dai punti interni alla circonferenza
La distanza viene definita come nel modello di Klein
CONCLUSIONI
Tramite queste interpretazioni i postulati della geometria iperbolica diventano teoremi della
geometria euclidea, e per questo motivo ogni contraddizione eventualmente deducibile dai
postulati iperbolici potrebbe essere tradotta, ricorrendo a questo "dizionario", in una
contraddizione deducibile dai teoremi euclidei corrispondenti.
Ma poiché la nostra ipotesi è che non vi siano contraddizioni nella geometria euclidea, non ve ne
saranno nemmeno in quella iperbolica.
Possiamo concludere che la geometria iperbolica è coerente solo se lo è quella euclidea.
Vale anche il viceversa: la geometria euclidea è coerente solo se lo è quella iperbolica, quindi
l'affermazione diventa più forte, e ci permette di stabilire una perfetta equivalenza delle due
geometrie rispetto al requisito di non contraddittorietà.
Riflettiamo ancora:
cosa possiamo rispondere alla secolare questione del V postulato, e cioè se il V postulato sia
deducibile dalla geometria neutrale?
Se la geometria euclidea è coerente, la risposta è no!
Se il V postulato fosse conseguenza logica degli altri 4 postulati, ovvero della geometria
neutrale, ogni insieme di enti che soddisfa tali proposizioni dovrebbe soddisfare anche il V
postulato. Ma abbiamo appena visto che gli enti del modello di Klein
(o di Poincarè )soddisfano tutti gli altri assiomi e non il V postulato.
14
UN MODELLO PER LA GEOMETRIA ELLITTICA
Nella geometria euclidea, così come in quella di Lobacewskij si implica, seppur tacitamente, che
la retta è infinita, ma con Riemann si apre una nuova via di intendere i concetti fondamentali.
Egli infatti fu il primo a introdurre una distinzione tra illimitatezza e infinità; tale distinzione gli
derivava dal considerare in geometria sia le proprietà di "estensione" sia le proprietà "metriche" e
affermava che l'illimitatezza dello spazio possiede una maggiore certezza empirica di ogni altra
esperienza esterna, ma che da questo non consegue necessariamente l'infinità, anzi basterebbe
che lo spazio avesse una curvatura costante positiva, seppur minima, ed esso sarebbe
certamente finito.
Riemann abbandona quindi la tradizionale concezione euclidea dello spazio inteso soprattutto in
senso sintetico (strettamente geometrico) e lo integra con visione più analitica ( più rivolta verso
il calcolo).
Nella teoria di Riemann è di fondamentale importanza il concetto di varietà n-dimensionale, che
porta ad una generalizzazione del piano e dello spazio cartesiano.
Per meglio spiegare la sua teoria Riemann utilizza come modello una superficie curva, da cui
nasce l'esigenza di introdurre un valore di curvatura dello spazio.
Secondo tale valore si possono distinguere tre varietà a curvatura costante:
a) varietà a curvatura negativa (geometria di Lobacewskij o iperbolica)
b) varietà a curvatura nulla (geometria di Euclide)
c) varietà a curvatura positiva (geometria di Riemann o ellittica)
L'ultimo caso è quello di cui si occupa Riemann ed è fondato essenzialmente sull'ipotesi che la
retta sia chiusa e finita.
Il modello che Riemann propone è il seguente:
Il piano è costituito da una superficie chiusa ( per comodità potremmo pensare ad una
superficie sferica)
I punti sono coppie di punti diametralmente opposti
Le rette per due punti sono i cerchi massimi passanti per essi
É evidente che in questo modello non esistono rette parallele.
In tale contesto Riemann definisce la linea di minima distanza tra due punti la
geodetica, cioè l'arco minore di circonferenza che passa per i due punti ed ha il
Centro nel centro della sfera. A volte, per semplificare il modello si preferisce
considerare una semisfera, per evitare il caso di punti diametralmente opposti sulla
sfera.
15
In questa geometria, oltre alla non esistenza di rette parallele, si può dimostrare
che:
- la somma degli angoli interni di un triangolo è sempre maggiore di una angolo
piatto
- non esistono triangoli simili, salvo quando sono anche congruenti
- tutte le perpendicolari ad una "retta" passano per una medesima coppia di punti,
che sono diametralmente opposti.
Come si può ben capire dalla figura precedente non è più valida l'unicità della retta
perpendicolare ad una retta data e passante per un punto (la "retta" che passa per A e per B ha
come perpendicolari sia la retta AC che la retta BC, entrambe passanti per C).
Inoltre, pensando di aumentare la lunghezza dell'arco AB e mantenendo fisso il vertice C, si
possono ottenere triangoli in cui la somma degli angoli interni può arrivare fino a 540°.
16