Trasformazioni termodinamiche - problema

Trasformazione isotermica (T = costante)
TRASFORMAZIONE ISOTERMICA
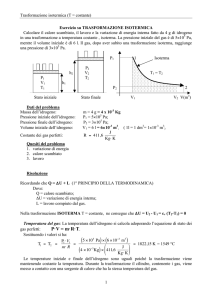
Calcolare il calore scambiato, il lavoro e la variazione di energia interna fatto da 4 g di idrogeno
in una trasformazione a temperatura costante , isoterma. La pressione iniziale del gas è di 5105 Pa,
mentre il volume iniziale è di 6 l. Il gas, dopo aver subito una trasformazione isoterma, raggiunge
una pressione di 3105 Pa.
P1
P2
V2
T2
h2
P1
V1
T1
1
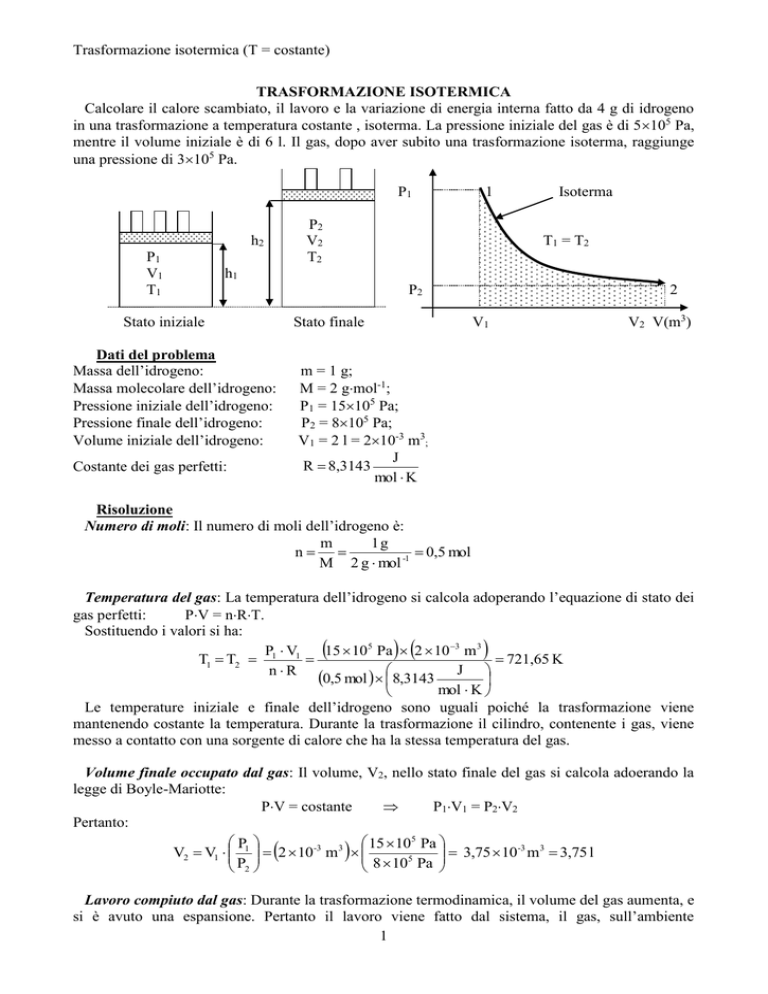
Isoterma
T1 = T2
h1
P2
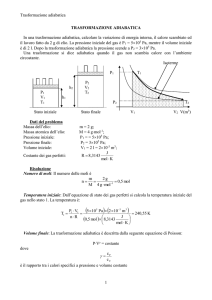
Stato iniziale
Stato finale
Dati del problema
Massa dell’idrogeno:
Massa molecolare dell’idrogeno:
Pressione iniziale dell’idrogeno:
Pressione finale dell’idrogeno:
Volume iniziale dell’idrogeno:
Costante dei gas perfetti:
2
V1
V2 V(m3)
m = 1 g;
M = 2 gmol-1;
P1 = 15105 Pa;
P2 = 8105 Pa;
V1 = 2 l = 210-3 m3;
J
R  8,3143
mol  K
Risoluzione
Numero di moli: Il numero di moli dell’idrogeno è:
m
1g
n 
 0,5 mol
M 2 g  mol -1
Temperatura del gas: La temperatura dell’idrogeno si calcola adoperando l’equazione di stato dei
gas perfetti:
PV = nRT.
Sostituendo i valori si ha:
P V
15  105 Pa  2  10 3 m 3
T1  T2  1 1 
 721,65 K
J 
nR

0,5 mol    8,3143

mol  K 

Le temperature iniziale e finale dell’idrogeno sono uguali poiché la trasformazione viene
mantenendo costante la temperatura. Durante la trasformazione il cilindro, contenente i gas, viene
messo a contatto con una sorgente di calore che ha la stessa temperatura del gas.

 

Volume finale occupato dal gas: Il volume, V2, nello stato finale del gas si calcola adoerando la
legge di Boyle-Mariotte:
PV = costante

P1V1 = P2V2
Pertanto:
P 
 15  105 Pa 
  3,75  10-3 m3  3,75 l
V2  V1   1   2  10-3 m3  
5
P
8

10
Pa


 2


Lavoro compiuto dal gas: Durante la trasformazione termodinamica, il volume del gas aumenta, e
si è avuto una espansione. Pertanto il lavoro viene fatto dal sistema, il gas, sull’ambiente
1
Trasformazione isotermica (T = costante)
circostante, innalzamento del pistone. Il valore del lavoro compiuto dal gas nel passare adllo stato 1
allo stato 2 è:
V 
P 
L12  n  R  T1  ln  2   n  R  T1  ln  1 
 V1 
 P2 
 15 105 Pa 
J 

   1885,826 J
L12  0,5 mol   8,3143
  721,65K  ln 
5
mol  K 

 8 10 Pa 
La parte tratteggiata sotto la curva, che indica la isoterma, rappresenta il lavoro compiuto.
Calore scambiato: Il calore scambiato fra il gas e la sorgente di calore viene calcolato adoperando
il primo principio della termodinamica. Tale principio rappresenta il principio di conservazione
dell’energia e si scrive:
E = U + L
Dove:
E = calore scambiato;
U = variazione di energia interna;
L = lavoro compiuto dal gas.
In una trasformazione isoterma l’energia interna non cambia (U = 0), pertanto si ha:
E=L
quindi
E12 = L12 = + 1885,826 J
Il calore scambiato è positivo, ciò significa che la sorgente di calore cede energia al gas che si sta
espandendo a temperatura costante.
Da quest’ultima affermazione si può sottolineare come il calore e la temperatura siano due
concetti diversi tra di loro e di come non ci sia sempre una corrispondenza automatica tra
assorbimento di calore ed innalzamento della temperatura.
2