Trasformazioni termodinamiche - problemi risolti

Trasformazione a pressione costante (P = cost.)
VARIAZIONE DELL’ENERGIA INTERNA IN UNA TRASFORMAZIONE A PRESSIONE
COSTANTE (P = cost.)
Un cilindro contiene 2 g di elio (gas monoatomico) alla pressione P1 = 5105 Pa. Il volume
occupato dal gas è di 2 litri.
Mantenendo costante la pressione, il gas subisce una espansione termica dopo che è stato messo a
contatto con una sorgente di calore. Il volume finale del gas è di 8 litri.
Calcolare il calore scambiato, lavoro compiuto dal gas e la variazione di energia interna.
P (Pa)
P1
V1
T1
P2
V2
T2
h2
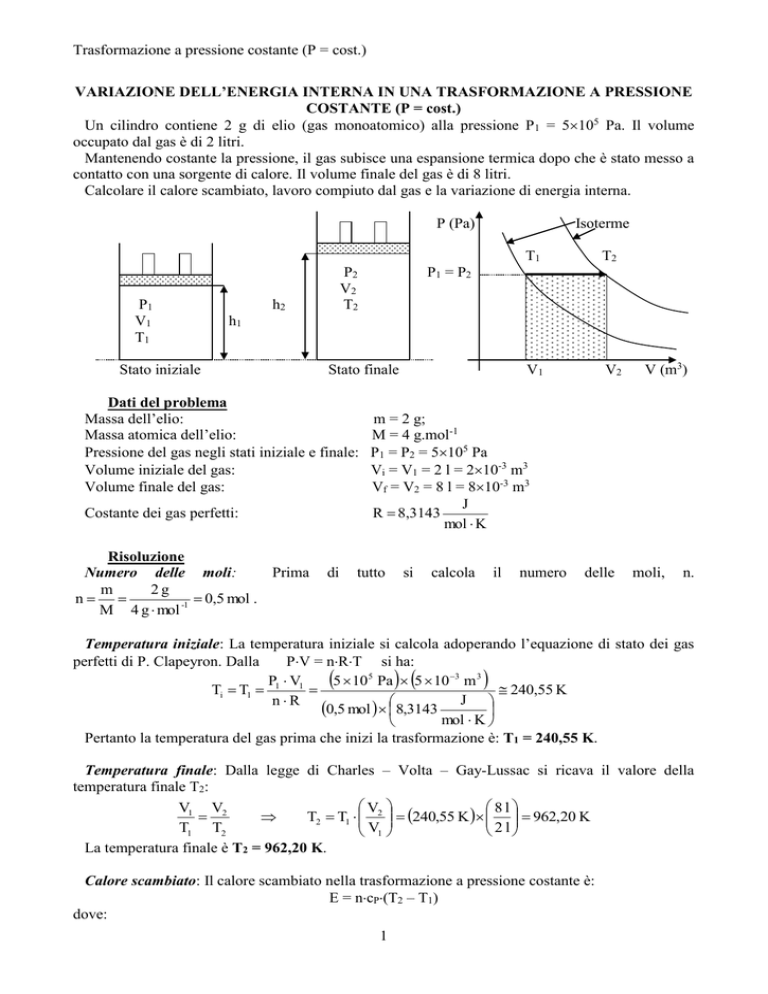
Isoterme
T1
T2
V1
V2
P1 = P2
h1
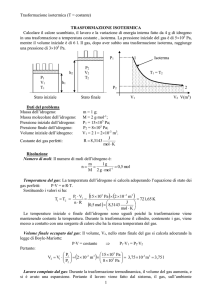
Stato iniziale
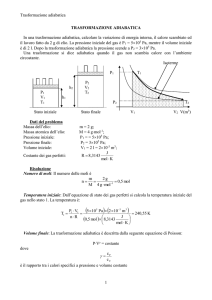
Stato finale
Dati del problema
Massa dell’elio:
Massa atomica dell’elio:
Pressione del gas negli stati iniziale e finale:
Volume iniziale del gas:
Volume finale del gas:
Costante dei gas perfetti:
Risoluzione
Numero delle moli:
Prima
m
2g
n 
 0,5 mol .
M 4 g  mol -1
di
V (m3)
m = 2 g;
M = 4 g.mol-1
P1 = P2 = 5105 Pa
Vi = V1 = 2 l = 210-3 m3
Vf = V2 = 8 l = 810-3 m3
J
R  8,3143
mol  K
tutto
si
calcola
il
numero
delle
moli,
n.
Temperatura iniziale: La temperatura iniziale si calcola adoperando l’equazione di stato dei gas
perfetti di P. Clapeyron. Dalla
PV = nRT si ha:
P1  V1
5  105 Pa  5  10 3 m 3
Ti  T1 

 240,55 K
J 
nR

0,5 mol    8,3143

mol  K 

Pertanto la temperatura del gas prima che inizi la trasformazione è: T1 = 240,55 K.

 

Temperatura finale: Dalla legge di Charles – Volta – Gay-Lussac si ricava il valore della
temperatura finale T2:
V 
8l
V1 V2


T2  T1   2   240,55 K     962,20 K
T1 T2
2l
 V1 
La temperatura finale è T2 = 962,20 K.
Calore scambiato: Il calore scambiato nella trasformazione a pressione costante è:
E = ncP(T2 – T1)
dove:
1
Trasformazione a pressione costante (P = cost.)
n è il numero delle moli;
cP è il calore specifico molare (cioè riferito ad una mole di gas) a pressione costante.
Per un gas monoatomico, come l’elio, il calore specifico a pressione costante è:
5
5 
J 
J
c P   R    8,3143
  20,7858
2
2 
mol  K 
mol  K
Sostituendo i valori di n e di cP si ha:
J 

E = ncP(T2 – T1) = 0,5 mol   20,7858
  962,20 K  - 240,55 K    7500 J
mol  K 

Il valore del calore scambiato è positivo, quindi esso è stato assorbito dal gas durante la
trasformazione termodinamica.
Lavoro compiuto: Prima che iniziasse la trasformazione isobara, il pistone si trova ad un’altezza
h1 dal fondo del cilindro. Alla fine della trasformazione il pistone si trova ad una altezza h2.
Pertanto il pistone ha subito uno spostamento pari a:
s = h2 – h1
Sul pistone agisce una forza dovuta agli urti degli atomi di elio contro il pistone. Durante la


trasformazione agisce una forza F per uno spostamento  s , pertanto viene compiuto un lavoro L
pari a:
 
L = F   s = F(h2 – h1)
F

Indicando con A la superficie del pistone e tenendo presente la definizione di pressione  P  
A

si ha che
F = PA
Sostituendo tale quantità nell’espressione del lavoro, si ha:
L = F(h2 – h1) = PA(h2 – h1) = P[Ah2 – Ah1]
La quantità Ah2 è il volume finale del gas:
V2 = Ah2
mentre Ah1 è il volume iniziale
V1 = Ah1
Pertanto il lavoro compiuto dal gas nell’andare dalla stato 1 allo stato 2 è
L12 = P(V1 – V2) = PV
Introducendo i valori si ha:
L12 = (5105 Pa)[(810-3 m3) – (210-3 m3)] = (5105 Pa)(610-3 m3) = + 3.000 J
Il valore del lavoro è positivo (espansione el gas), per cui il lavoro è compiuto dal gas
sull’ambiente circostante
L12 = + 3.000 J
La parte tratteggiata sotto la curva rappresenta il lavoro compiuto.
Variazione dell’energia interna: Applicando il primo principio della termodinamica si può
ricavare la variazione di energia interna subita dal gas:
U = E – L = (+ 7.500 J) – (+ 3.000 J) = + 4.500 J
La variazione di energia interna è positiva. Poiché l’energia interna è una grandezza collegata
alla temperatura del gas, il risultato (l’energia interna è aumentata) è concorde con il fatto che
durante la trasformazione la temperatura aumenta.
Se il gas fosse stato biatomico, il calore specifico a pressione costante sarebbe:
7
J
c P   R  29,10
2
mol  K
2