trasformazione adiabatica

Trasformazione adiabatica
TRASFORMAZIONE ADIABATICA
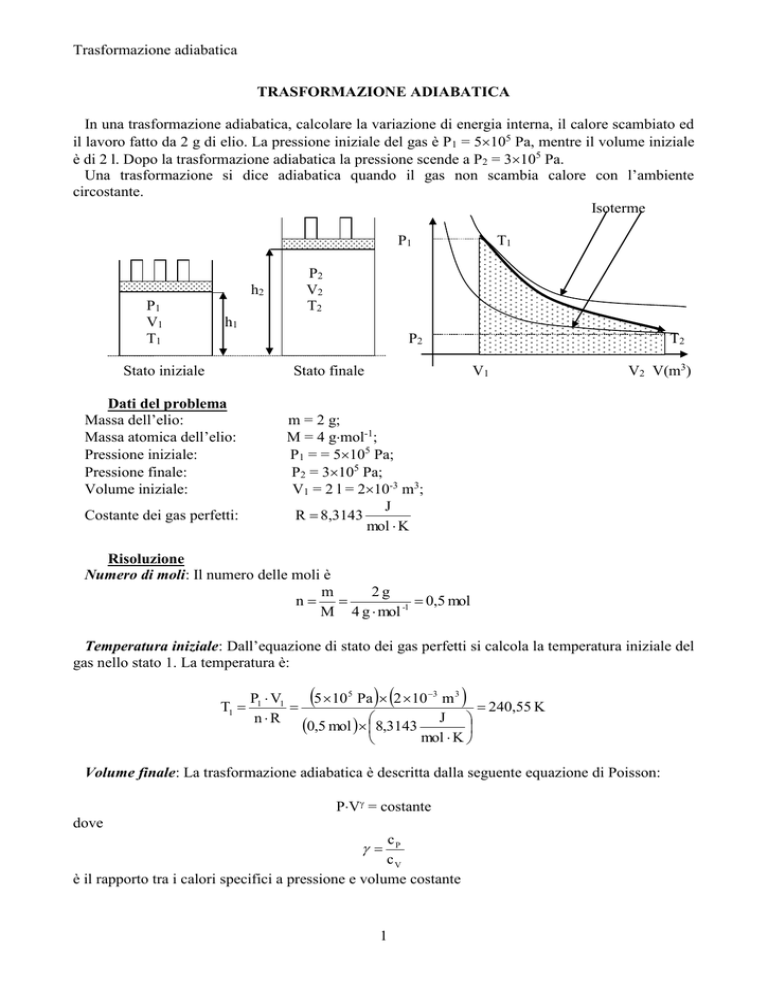
In una trasformazione adiabatica, calcolare la variazione di energia interna, il calore scambiato ed
il lavoro fatto da 2 g di elio. La pressione iniziale del gas è P1 = 5105 Pa, mentre il volume iniziale
è di 2 l. Dopo la trasformazione adiabatica la pressione scende a P2 = 3105 Pa.
Una trasformazione si dice adiabatica quando il gas non scambia calore con l’ambiente
circostante.
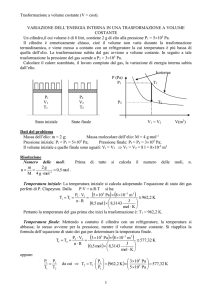
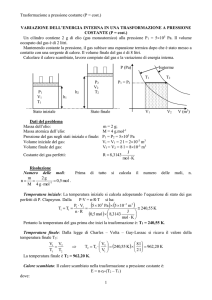
Isoterme
P1
P2
V2
T2
h2
P1
V1
T1
T1
h1
P2
Stato iniziale
T2
Stato finale
Dati del problema
Massa dell’elio:
Massa atomica dell’elio:
Pressione iniziale:
Pressione finale:
Volume iniziale:
Costante dei gas perfetti:
V1
V2 V(m3)
m = 2 g;
M = 4 gmol-1;
P1 = = 5105 Pa;
P2 = 3105 Pa;
V1 = 2 l = 210-3 m3;
J
R  8,3143
mol  K
Risoluzione
Numero di moli: Il numero delle moli è
m
2g
n 
 0,5 mol
M 4 g  mol -1
Temperatura iniziale: Dall’equazione di stato dei gas perfetti si calcola la temperatura iniziale del
gas nello stato 1. La temperatura è:
T1 
P1  V1

nR
5 10
 

Pa  2 10 3 m 3
 240,55 K
J 

0,5 mol   8,3143

mol  K 

5
Volume finale: La trasformazione adiabatica è descritta dalla seguente equazione di Poisson:
PV = costante
dove
cP
cV
è il rapporto tra i calori specifici a pressione e volume costante

1
Trasformazione adiabatica
Gas monoatomico
5
cP   R
2
3
cV   R
2
5

3
Calore specifico a pressione
costante
Calore specifico a volume
costante
Gas biatomico
7
cP   R
2
5
cV   R
2
7

5
L’equazione del gas nei due stati 1 e 2 è:

P1V1
=
P1V1
 V2 
P
   1
P2
 V1 

da cui si ricava
V2
P
P
  1  V2  V1   1
V1
P2
P2
Sapendo che l’elio è un gas monoatomico, si sostituiscono i relativi valori:
5 10 5 Pa
5
V2  2 10 m 
 2 10 -3 m 3  5    2 10 -3 m 3  1,358655  2,72 10 -3 m 3
5
3 10 Pa
3
Quindi il volume del gas nello stato finale 2 è:
V2 = 2,7210-3 m3 = 2,72 l

-3
3

5
3

3



Temperatura nello stato finale 2: La temperatura dell’elio nello stato finale 2 si ricava
dall’equazione di stato dei gas perfetti:
P2  V2 3 10 5 Pa  2,72 10 3 m 3 
T2 

 196,28 K
J 
nR

0,5 mol   8,3143

mol  K 

Variazione dell’energia interna: In una trasformazione termodinamica la variazione di energia
interna è:
U12 = ncV(T2 – T1)
Sostituendo i valori si ha:
J 
3
U12  0,5 mol    8,3143
  196,28 K  - 240,55 K   - 276,05 J
mol  K 
2
L’energia interna è diminuita, come era prevedibile dal momento che la temperatura è anch’essa
diminuita.
Lavoro compiuto dal gas: Il gas subisce una espansione (il volume dello stato finale 2 è più
grande di quello iniziale 1), pertanto il sistema, cioè il gas, compie un lavoro positivo sull’ambiente
circostante.
La trasformazione è adiabatica, quindi il calore scambiato con l’ambiente circostante è nullo:
E=0J
pertanto il primo principio della termodinamica si riduce a:
U12 = - L12
infatti:
U = E - L = - L
Sostituendo i valori si ha:
L12 = - U12 = - (-276,05 J) = + 276,05 J
2