Trasformazione isotermica (T = costante)
Esercizio su TRASFORMAZIONE ISOTERMICA
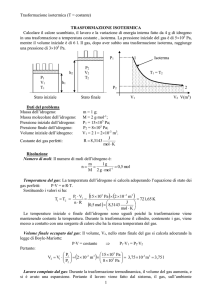
Calcolare il calore scambiato, il lavoro e la variazione di energia interna fatto da 4 g di idrogeno
in una trasformazione a temperatura costante , isoterma. La pressione iniziale del gas è di 5×105 Pa,
mentre il volume iniziale è di 6 l. Il gas, dopo aver subito una trasformazione isoterma, raggiunge
una pressione di 3×105 Pa.
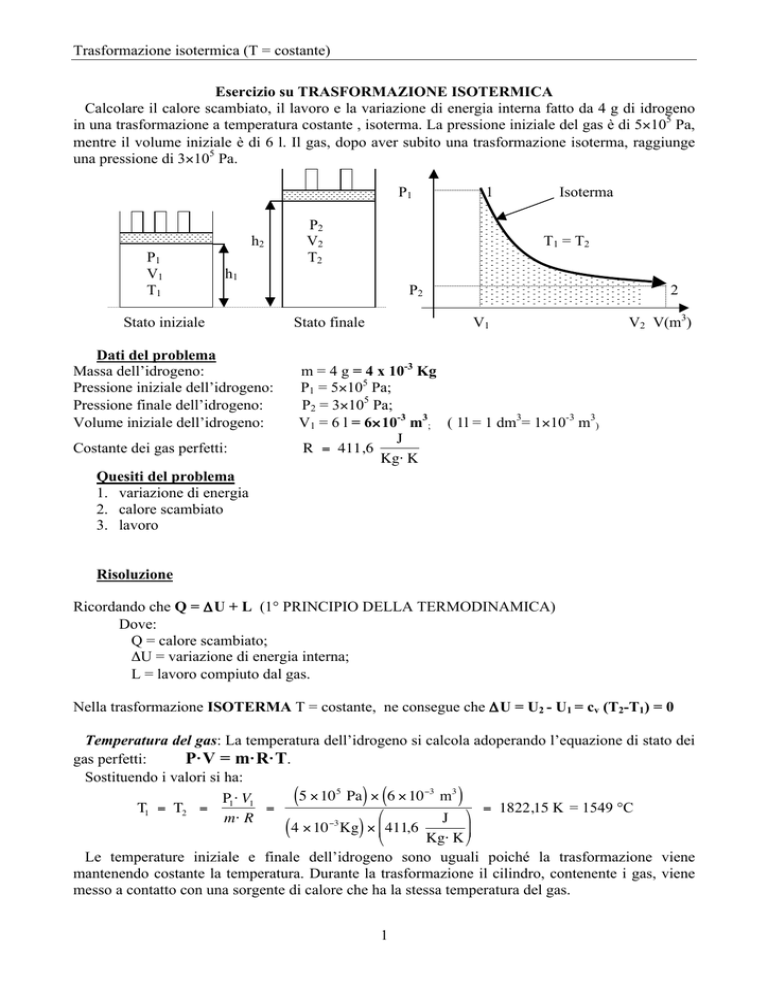
P1
h2
P1
V1
T1
h1
Stato iniziale
Dati del problema
Massa dell’idrogeno:
Pressione iniziale dell’idrogeno:
Pressione finale dell’idrogeno:
Volume iniziale dell’idrogeno:
Costante dei gas perfetti:
1
P2
V2
T2
Isoterma
T1 = T2
P2
Stato finale
2
V1
V2 V(m3)
m = 4 g = 4 x 10-3 Kg
P1 = 5×105 Pa;
P2 = 3×105 Pa;
V1 = 6 l = 6×10-3 m3; ( 1l = 1 dm3= 1×10-3 m3)
J
R = 411,6
Kg⋅ K
Quesiti del problema
1. variazione di energia
2. calore scambiato
€
3. lavoro
Risoluzione
Ricordando che Q = ΔU + L (1° PRINCIPIO DELLA TERMODINAMICA)
Dove:
Q = calore scambiato;
ΔU = variazione di energia interna;
L = lavoro compiuto dal gas.
Nella trasformazione ISOTERMA T = costante, ne consegue che ΔU = U2 - U1 = cv (T2-T1) = 0
Temperatura del gas: La temperatura dell’idrogeno si calcola adoperando l’equazione di stato dei
gas perfetti:
P⋅V = m⋅R⋅T.
Sostituendo i valori si ha:
5 × 10 5 Pa) × (6 × 10 −3 m3 )
(
P1 ⋅ V1
T1 = T2 =
=
= 1822,15 K = 1549 °C
⎛
m⋅ R
J ⎞
−3
(4 × 10 Kg) × ⎜⎝ 411,6 Kg⋅ K ⎟⎠
Le temperature iniziale e finale dell’idrogeno sono uguali poiché la trasformazione viene
mantenendo costante la temperatura. Durante la trasformazione il cilindro, contenente i gas, viene
messo a contatto con una sorgente di calore che ha la stessa temperatura del gas.
€
1
Trasformazione isotermica (T = costante)
€
Lavoro compiuto dal gas: Durante la trasformazione termodinamica, il volume del gas aumenta, e
si è avuto una espansione. Pertanto il lavoro viene fatto dal sistema, il gas, sull’ambiente
circostante, innalzamento del pistone. Il valore del lavoro compiuto dal gas nel passare dallo stato 1
allo stato 2 è:
⎛ V ⎞
⎛ P ⎞
⎛ P ⎞
L1→ 2 = m⋅ R⋅ T1 ⋅ ln⎜ 2 ⎟ = m⋅ R⋅ T1 ⋅ ln⎜ 1 ⎟
poiché P1⋅V1 = P2⋅V2 e quindi V2 = V1 ⋅ ⎜ 1 ⎟
⎝ V1 ⎠
⎝ P2 ⎠
⎝ P2 ⎠
5
⎛ 5 × 10 Pa ⎞
⎛
J ⎞
L1→ 2 = ( 4x10 −3 Kg) × ⎜ 411,6
⎟ = + 4999,97 J
⎟ × (1822,15K) × ln⎜
5
Kg⋅ K ⎠
⎝
⎝ 3 × 10 Pa ⎠
La parte tratteggiata sotto la curva, che indica la isoterma, rappresenta il €
lavoro compiuto.
Calore scambiato: Il calore scambiato fra il gas e la sorgente di calore viene calcolato adoperando
€ il primo principio della termodinamica. Tale principio rappresenta il principio di conservazione
dell’energia e si scrive:
Q = ΔU + L
Dove:
Q = calore scambiato;
ΔU = variazione di energia interna;
L = lavoro compiuto dal gas.
In una trasformazione isoterma l’energia interna non cambia (ΔU = 0), pertanto si ha:
Q=L
quindi
Q1 2 = L1 2 = + 4999,97 J
Il calore scambiato è positivo, ciò significa che la sorgente di calore cede energia al gas che si sta
espandendo a temperatura costante.
Da quest’ultima affermazione si può sottolineare come il calore e la temperatura siano due
concetti diversi tra di loro e di come non ci sia sempre una corrispondenza automatica tra
assorbimento di calore ed innalzamento della temperatura.
→
→
Volume finale occupato dal gas: Il volume, V2, nello stato finale del gas si calcola adoerando la
legge di Boyle-Mariotte:
P⋅V = costante
⇒
P1⋅V1 = P2⋅V2
Pertanto:
⎛ P1 ⎞
⎛ 5 × 10 5 Pa ⎞
-3
3
-3 3
3
V2 = V1 ⋅ ⎜ ⎟ = (6 × 10 m ) × ⎜
⎟ = 10 × 10 m = 0,01 m = 10 l
5
⎝ 3 × 10 Pa ⎠
⎝ P2 ⎠
€
2