Trasformazioni termodinamiche - problema

Trasformazione a volume costante (V = cost).
VARIAZIONE DELL’ENERGIA INTERNA IN UNA TRASFORMAZIONE A VOLUME
COSTANTE
Un cilindro,il cui volume è di 8 litri, contiene 2 g di elio alla pressione P1 = 5105 Pa.
Il cilindro è ermeticamente chiuso, cioè il volume non varia durante la trasformazione
termodinamica, e viene messo a contatto con un refrigeratore la cui temperatura è più bassa di
quella dell’elio. La trasformazione subita dal gas avviene a volume costante. In seguito a tale
trasformazione la pressione del gas scende a P2 = 3105 Pa.
Calcolare il calore scambiato, il lavoro compiuto dal gas, la variazione di energia interna subita
dall’elio.
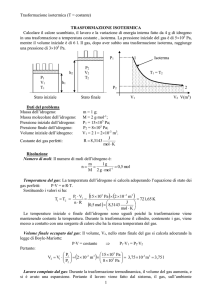
Isoterme
P (Pa)
P1
T1
P1
V1
T1
P2
V2
T2
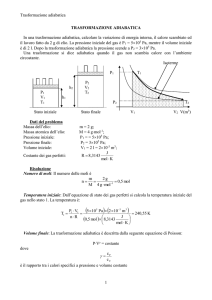
Stato iniziale
Stato finale
P2
T2
V(m3)
V 1 = V2
Dati del problema
Massa dell’elio: m = 2 g;
Massa molecolare dell’elio: M = 4 gmol-1
Pressione iniziale: Pi = P1 = 5105 Pa;
Pressione finale: Pf = P2 = 3105 Pa;
Il volume iniziale e quello finale sono uguali: Vi = Vf  V1 = V2 = 8 l = 810-3 m3
Risoluzione
Numero delle moli:
Prima
m
2g
n 
 0,5 mol .
M 4 g  mol -1
di
tutto
si
calcola
il
numero
delle
moli,
n.
Temperatura iniziale: La temperatura iniziale si calcola adoperando l’equazione di stato dei gas
perfetti di P. Clapeyron. Dalla
PV = nRT si ha:
P V
5  105 Pa  8  10 3 m 3
Ti  T1  1 1 
 962,2 K
J 
nR

0,5 mol    8,3143

mol  K 

Pertanto la temperatura del gas prima che inizi la trasformazione è: T1 = 962,2 K.

 

Temperatura finale: Mettendo a contatto il cilindro con un refrigeratore, la temperatura si
abbassa; lo stesso avviene per la pressione, mentre il volume rimane costante. Si riapplica la
formula dell’equazione di stato dei gas per determinare la temperatura finale.
P V
3  105 Pa  8  10 3 m 3
Tf  T2  2 2 
 577,32 K
J 
nR

0,5 mol    8,3143

mol  K 

oppure:
P 
 3 105 Pa 
P1 P2
  577,32 K

da cui  T2  T1   2   962,2 K  
5
T1 T2
P
5

10
Pa


 1

 
1

Trasformazione a volume costante (V = cost).
Calore scambiato: Il calore scambiato nella trasformazione a volume costante è:
E = ncV(T2 – T1)
Dove: cV è il calore specifico molare (cioè riferito ad una mole di gas) a volume costante.
Per un gas monoatomico, come l’elio, si ha:
3
3 
J 
J
c V   R    8,3143
  12,47145
2
2 
mol  K 
mol  K
Sostituendo i valori si ottiene:
J 

E = ncV(T2 – T1) = 0,5 mol  12,47
  577,32 K  - 962,20 K   - 2399,72 J
mol  K 

Il valore del calore scambiato è negativo, ciò sta a significare che il gas ha ceduto calore
all’ambiente circostante (il refrigeratore).
Lavoro compiuto dal gas: Poiché il volume del gas non cambia /trasformazione a V = cost), il
lavoro compiuto dal gas è nullo:
L = 0 J.
Variazione dell’energia interna: Applicando il primo principio della termodinamica si può
ricavare la variazione di energia interna subita dal gas:
U = E – L = (-2399,72 j) – (0 J) = - 2399,72 J  -2400 J
L’energia interna, come era prevedibile, è diminuita, dal momento che la temperatura è
diminuita.
Se il gas fosse stato biatomico, il calore specifico a volume costante sarebbe:
5
J
c V   R  20,7858
2
mol  K
2