24.06.02

Prova scritta dell’esame di TEORIA DEI SEGNALI
COMPITO B
24/06/02
Esercizio1.
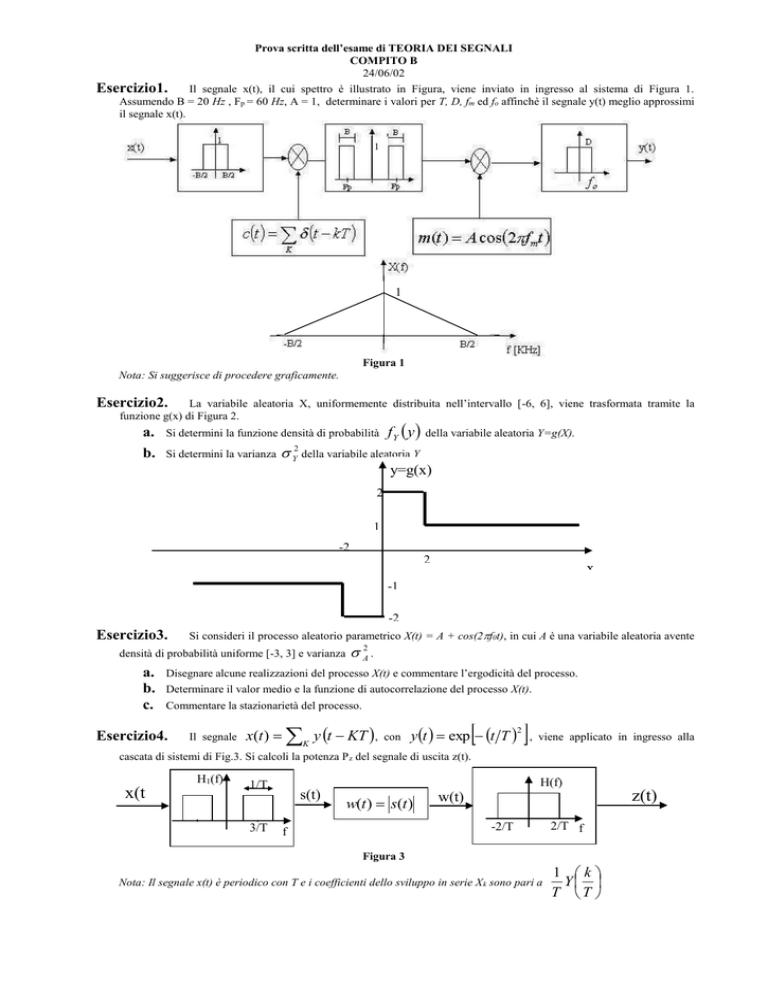
Il segnale x(t), il cui spettro è illustrato in Figura, viene inviato in ingresso al sistema di Figura 1.
Assumendo B = 20 Hz , Fp = 60 Hz, A = 1, determinare i valori per T, D, fm ed fo affinchè il segnale y(t) meglio approssimi
il segnale x(t).
1
1
Figura 1
Nota: Si suggerisce di procedere graficamente.
Esercizio2.
La variabile aleatoria X, uniformemente distribuita nell’intervallo [-6, 6], viene trasformata tramite la
funzione g(x) di Figura 2.
a.
b.
Si determini la funzione densità di probabilità
Si determini la varianza

2
Y
f Y  y  della variabile aleatoria Y=g(X).
della variabile aleatoria Y
y=g(x)
2
1
-2
2
x
-1
-2
Esercizio3.
Si consideri il processo aleatorio parametrico X(t) = A + cos(2f0t), in cui A è una variabile aleatoria avente
densità di probabilità uniforme [-3, 3] e varianza
a.
b.
c.
 A2 .
Disegnare alcune realizzazioni del processo X(t) e commentare l’ergodicità del processo.
Determinare il valor medio e la funzione di autocorrelazione del processo X(t).
Commentare la stazionarietà del processo.
Esercizio4.
Il segnale
x(t )  K y t  KT  ,
con

y t   exp  t T 
2
, viene applicato in ingresso alla
cascata di sistemi di Fig.3. Si calcoli la potenza P z del segnale di uscita z(t).
H1(f)
x(t
)
H(f)
1/T
3/T
s(t)
w(t )  s(t )
z(t)
w(t)
-2/T
f
2/T f
Figura 3
Nota: Il segnale x(t) è periodico con T e i coefficienti dello sviluppo in serie X k sono pari a
1 k
Y 
T T 
Xf 
Esercizio 1:

B
2
f
B
2
B
Il segnale xt  attraversa un filtro passa basso ideale con banda passate pari
quindi in uscita
2


x
t
otteniamo il segnale
troncato a B 2
X1  f 
1
x1 t 
X 1  f   H1  f   X

f 
A questo punto il segnale
x1 t 
B
2
f
B
2
viene campionato con periodo pari a T con T 
1
B
1
X 2  f   C  f   X 1  f      f  KF   X 1  f   F X 1  f  KF 
K T
K
x1 t 
1
T
x2 t 

X2 f 
B
2
B
2
2B
B
f
Quindi lo spettro di x2 t  è costituito dalle repliche traslate dello spettro di x1 t a meno del fattore F
con F=1/T
Il segnale x2 t  attraversa un filtro passabanda con frequenza di centro banda pari a FP
X3 f 
H2  f 
x2 t 
x3 t 
X 3  f   H 2  f  X 2  f 
F
 FP
FP  n  B
f
Le
uniche
repliche
che
ritroviamo
F p  X 3  f   FX 2  f  Fp   FX 2  f  Fp 
in
uscita
sono
quelle
centrate
in
Il segnale mt  viene modulato da x3 t  .Scelgo f m  F p per ottenere una replica centrata in f=0.
X 4  f   M  f  X 3  f  
x3 t 
A
  f  f m     f  f m  X 3  f   A X 3  f  f m   X 3  f  f m 
2
2
x4 t 
1
A
T
f m  FP
 FP  f m
 FP
Y  f   H 3  f X 4  f   rect 2 f o  f X 4  f  Scelgo

B
2
fo 
B
2
Infine per ottenere il segnale originario si deve
1porre
T
 A D 1 D  T
B
2
FP  f m
FP
B
2
1
 A D
T

X4 f 
Y f 
B
2
f
f
Esercizio 2
a) La variabile aleatoria Y è discreta ed assume solamente i valori  1,2 . La sua densità di
probabilità sarà quindi data da
f y  y   p  2  y  2  p 1  y  1  p1  y  1  p 2  y  2
f X x 
dove si è definito
1
12
pi  PrY  i
6
x
6
1
Tenuto conto delle particolari simmetrie della densità di probabilità della X e della trasformazione
g x , si osserva inoltre che
p 2  p2
p1  p1
da cui si ha
p1
fY  y 
p1
p2
f y y 
1
  y  1    y  1  1   y  2    y  2
3
6
2
p2
1
1
2
Le probabilità sono date da
6
p1  PrY  1  PrX  2   f X  x dx  1
2
3
2
p2  PrY  2  Pr0  X  2   f X x dx  1
0
6
b) Il valor medio di Y è evidentemente nullo per la simmetria, per cui la varianza è data da
 Y2  EY 2   p 2  22  p 1  12  p 2 22  p1 12
y
Esercizio 3
a)
X t 
t
La media temporale di ciascuna realizzazione è pari al valore assunto della v.a A,  ciascuna
realizzazione ha un valor medio temporale diverso  IL PROCESSO NON può essere ERGODICO
IN MEDIA.
b) Determiniamo il valor medio del processo X t 
EX t   EA  cos2f o t   EA  cos2f o t   cos2f o t 
EA  0 poiché la f.d.p. è simmetrica rispetto all’origine
La funzione di autocorrelazione è data da
RX t1,t2   EX t1 X t2   EA  cos2f ot1 A  cos2f ot2  
 
 E A2  cos2f ot1 EA  cos2f ot2 EA  cos2f ot1 cos2f ot2  
  A2  cos2f ot1 cos2f ot2 
  EA  EA  EA    a f A a da   a 2 da 
3
2
A
2
2
2
3
2
3
3
1
6
1 54 54
 3
6 3 18
c) Il processo non è stazionario neppure in media poiché Ex dipende da t.
Esercizio 4
x(t) periodico con periodo T segue che la TCF di x(t) è un treno d’impulsi
Xf 
X0


X  f    X K  f  K
XK
T
X1
1
T
1
2

T
T
2
T
3
T
4
T
5
T
6
T
f

 
K2
 2T 2 2
2
1
T
T
 Y K 

e
  e K 
T T
T
dato
che
 t
Y  f   F e


 2T 2 f 2
   Te

2
T2
X K  X K
Il primo filtro lascia passare solo la terza armonica di x(t). Si ha allora che

S  f   H 1  f   X  f   X 3 f  3
3 

st   2 X 3 cos 2 t 
 T 
T
  X   f  3T 
3
segnale
periodico
di
T
3
periodo
Il segnale w(t) è allora dato da
3 

wt   2 X 3 cos 2 t 
 T 
periodico
Tw 
con
T
6
wt 
T
6

W  f   K WK  f  K 6
T

t
W f 
Wo
 18
T
T
3
 12
T
6
T
2
T
W1
2
T
6
T
12
T
18
T
f
Il secondo filtro lascia passare soltanto la componente continua del segnale w(t) cioè il valor medio
di w(t)
z t   wt  
z t  
4

T
12
 wt dt  T  2 X
 
1
TW
1
TW
T
6 12
 e  9  K
La potenza del segnale di uscita è allora
Pz  K 2 
16

e 18
2
3
3 
2 4

cos 2 t dt  2 X 3 
 e  9
 
 T 