11.09.02

Prova scritta dell’esame di TEORIA DEI SEGNALI
11/09/02
Esercizio1.
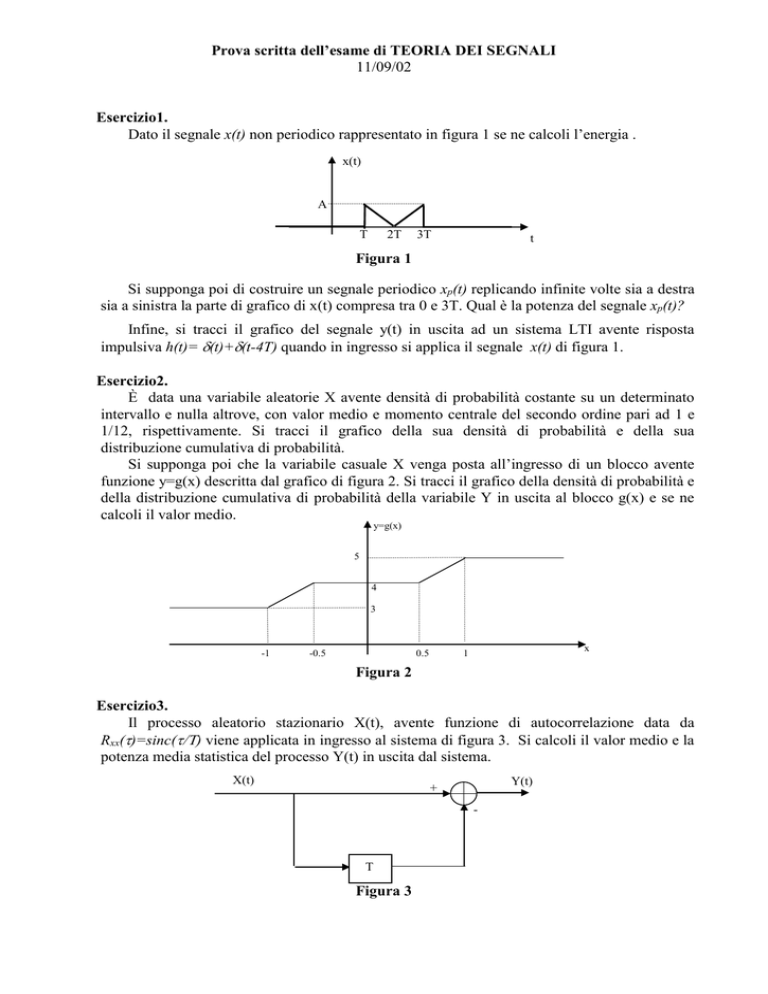
Dato il segnale x(t) non periodico rappresentato in figura 1 se ne calcoli l’energia .
x(t)
A
T
2T
3T
t
Figura 1
Si supponga poi di costruire un segnale periodico xp(t) replicando infinite volte sia a destra
sia a sinistra la parte di grafico di x(t) compresa tra 0 e 3T. Qual è la potenza del segnale xp(t)?
Infine, si tracci il grafico del segnale y(t) in uscita ad un sistema LTI avente risposta
impulsiva h(t)= (t)+(t-4T) quando in ingresso si applica il segnale x(t) di figura 1.
Esercizio2.
È data una variabile aleatorie X avente densità di probabilità costante su un determinato
intervallo e nulla altrove, con valor medio e momento centrale del secondo ordine pari ad 1 e
1/12, rispettivamente. Si tracci il grafico della sua densità di probabilità e della sua
distribuzione cumulativa di probabilità.
Si supponga poi che la variabile casuale X venga posta all’ingresso di un blocco avente
funzione y=g(x) descritta dal grafico di figura 2. Si tracci il grafico della densità di probabilità e
della distribuzione cumulativa di probabilità della variabile Y in uscita al blocco g(x) e se ne
calcoli il valor medio.
y=g(x)
5
4
3
-1
-0.5
0.5
x
1
Figura 2
Esercizio3.
Il processo aleatorio stazionario X(t), avente funzione di autocorrelazione data da
Rxx()=sinc() viene applicata in ingresso al sistema di figura 3. Si calcoli il valor medio e la
potenza media statistica del processo Y(t) in uscita dal sistema.
X(t)
Y(t)
+
-
T
Figura 3
Esercizio 1
L’energia di una porzione del segnale non dipende dalla sua posizione. Poiché, per semplificare i
calcoli, è possibile determinare l’energia del triangolo rettangolo largo T ed alto A e poi utilizzarla
come elemento base per il calcolo dell’energia di tutto il segnale.
Quindi:
T
E EQ  
0
-A
2
A 2 T 3 A 2T
A 
xt  dt    t  dt  2

T 
3
T 3
0
T
2
0
T
E rimane la stessa anche nel caso di segnale traslato o ribaltato rispetto ad uno degli assi.
Perciò l’energia del segnale è due volte il triangolo rettangolo  2  E EQ 
2 A 2T
9
La potenza media del segnale periodico che si ottiene replicando il tratto tra 0 e 3T del segnale st 
è semplicemente l’energia del segnale diviso per la lunghezza del periodo 3T  : P 
2 A2
9
Il segnale h(t) è composto da due funzioni delta, perciò la convoluzione di xt  con h(t) produce
due repliche del primo con l’origine traslata nelle posizioni delle delta e l’altezza moltiplicata per il
coefficiente della delta considerata:
y(t)
A
T
2T
3T
4T
yt   xt   ht   xt    t    t  4T   xt   xt  4T 
5T
6T
7T
t
Esercizio 2
f X x 
1
ba
a
b
x
 x  Ex 
ba
1
2


E x   x   
2
2
x
2

b  a

12

1
12
Nota :
 x2  E x 2   x 2

   x f x dx   x
E x2 
b
2
x

a
2
1
1 b 3  a 3 b 2  ab  a 2
dx 

ba
ba
3
3
b  a   b  a 
b  ab  a
 

3
4
12
2
2
2
2
2
x
quindi :
b  a
 2  1

2
 b  a   1
 12
12
a  2  b
b  0.5
b - a   -1 2b - 2  1  
soluz. non accetabile

2
a  1.5
b  a   1
a  2  b

b  a   1
a  2  b

b  2  b   1
a  2  1.5  0.5

b  1.5
f X x 
FX x 
1
0.5
1.5
x
0.5
1.5
f X x 
1
0.5
1.5
x
y=g(x)
5
4
3
-1
Y  g x 
-0.5
0.5
1.5
x
1
 4,5
f Y x 
0.5
4
5
y
PY  5  P(1  X  1.5)  0.5
Per
X  0.5 , 1 la trasforma zione g(x) è lineare y  2x  3
Per
X  4 , 5
f Y y  
1
 y - b  1  y -3 1
 y-3 
fX 
 1
  fX 
  rect 
a
 a  2  2  2
 2

cioè ottengo lo stesso andamento della f X x  ma variata in ampiezza e traslata.
Infine
FY  y 
1
0.5
4
5
y
Esercizio 3
1° Soluzione
Y t   X t   X t  T 
EY t   EX t   EX t  T   0 perchè X(t) è un processo stazionari o quindi v.m. costante

 
PY  RYY 0   E Y 2 t   E X t   X t  T 
2
 EX t  EX t  T   2EX t  T X t 
2
2

0
T 
 R XX 0   R XX 0  2 R XX T   2senc   2senc   2
T 
T 
2° Soluzione
Come prima cosa si determina la densità spettrale di potenza del processo X(t), trasformando la
funzione di autocorrelazione
 f 

S X  f   T  rect 
1 
 T
Si determina poi la risposta in frequenza complessiva H(f) del sistema :


yt   xt   xt  T   trasformando  Y  f   X  f   X  f   e  j 2  fT  1  e  j 2  fT X  f 
da cui si ricava
H  f   1  e  j 2  fT
Il modulo quadro della risposta in frequenza è dato da
H f 
2



 1  e  j 2  fT  1  e  j 2  fT  2  2 cos2  fT 
La potenza media statistica del processo Y(t) è infine data da

PY 
 SY  f df 


 SY  f  H  f  df 
2

1 2T
 T 2  2 cos2  fT df
1 2T
2