primo teorema di euclide

Primo Teorema di Euclide
PRIMO TEOREMA DI EUCLIDE
Primo teorema di Euclide: In un qualunque triangolo rettangolo il quadrato costruito su di un
cateto è equivalente ad un rettangolo le cui dimensioni sono l’ipotenusa e la proiezione del cateto
sull’ipotenusa.
Ipotesi:1) [ABC] triangolo rettangolo
2) Â = angolo retto
3) [AB] e [AC] = cateti
4) [BC] = ipotenusa
5) Q = [ACED] = quadrato
 [AC] = [AD] = [EC] = [DE]
6) [CH] = proiezione del
cateto [AC] sulla ipotenusa [CB]
7) R = [CHNM] = rettangolo
8) [BC] = [NH] = [CM]
9) [CH] = [MN]
Tesi: Il quadrato Q =[ACED] è
equivalente al rettangolo R =
[CHNM], cioè:
Q  R
Premessa: Il quadrato, Q, ed il
rettangolo,
R,
sono
due
parallelogrammi. Per verificare la loro equivalenza è necessario avere a disposizione un altro
parallelogrammo, P, tale da essere equivalente sia al quadrato sia al rettangolo. È necessario, perciò,
costruire il quadrato, il rettangolo ed il parallelogrammo che farà da tramite delle due figure in
esame.
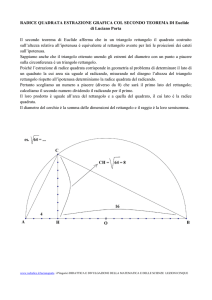
Costruzione: Sul cateto [AC] si costruisce il quadrato Q = [ACED].
Il segmento [CH] è la proiezione del cateto [AC] sull’ipotenusa [BC].
Sull’ipotenusa [BC] si costruisce il rettangolo R = [CHNM] le cui dimensioni sono:[CM] = [NH]
= [BC] = ipotenusa, e [CH] = [MN] = proiezione del cateto [AC] sulla ipotenusa [BC].
Si prolunga il lato [DE] del quadrato [ACDE], si ottiene il segmento [ES].
Si prolungano i lati paralleli, [CM] e [HN], del rettangolo R fino ad incontrare il segmento [ES] nei
punti F e G. In seguito a tale costruzione si è formato il quadrilatero P = [AGFC],che è un
parallelogrammo. Infatti, considerando la definizione di parallelogrammo (un quadrilatero è un
parallelogrammo se i suoi lati opposti sono paralleli) si ha: 1) i lati [FC] e [AG] sono paralleli per
costruzione (si prolungano i lati paralleli, [CM] e [HN], del rettangolo R fino ad incontrare il
segmento [ES] nei punti F e G); 2) i lati [FG] e [AC] sono paralleli poiché il lato [FG] si trova sul
prolungamento del segmento [ED], che, a sua volta, è parallelo a [AC] in quanto lati opposti del
quadrato Q.
Dimostrazione
1
Primo Teorema di Euclide
Prima parte
Nella prima parte si dimostrerà che il quadrato Q = [ACED] e il parallelogrammo P = [ACFG]
sono equivalenti (due parallelogrammi sono equivalenti se hanno la stessa base e la stessa altezza).
Infatti: 1) Il segmento [AC] è la base comune sia del quadrato Q sia del parallelogrammo P; 2) In
un parallelogrammo l’altezza è un segmento perpendicolare alla base ed indica anche la distanza fra
la base ed il lato opposto e parallelo. In questo caso se la base è il lato [AC], lato comune al
quadrato ed al parallelogrammo, allora l’altezza è il lato [AD]. Pertanto Il lato [AD] è altezza sia
del quadrato sia del parallelogrammo.
In conclusione il quadrato Q ed il parallelogrammo P hanno la stessa base, [AC], e la stessa altezza,
[AD], e, quindi, sono equivalenti (Q  P).
Seconda parte
Nella seconda parte si dimostrerà che il parallelogrammo P = [ACFG] è equivalente al rettangolo R
= [CHNM]. Anche in questo caso la equivalenza scaturirà dalla verifica che i due parallelogrammi
hanno la stessa base e la stessa altezza.
Per dimostrare che hanno la stessa base (il segmento [CM] per il rettangolo, ed il segmento [FC]
per il parallelogrammo) è necessario considerare i due triangoli [ABC] e [CEF].
[ABC]
[CEF]
 =
Ê
[AC] = [EC]
sono angoli retti per le ipotesi 2 e 5.
i due segmenti sono uguali per l’ipotesi 5.
 +  = angolo retto
  angolo retto - 

 =
 =

infatti: 
 +  = angolo retto  = angolo retto - 
I due triangoli, [ABC] e [CEF], per il secondo criterio di congruenza, sono congruenti. Essi, perciò,
 = F . Delle tre uguaglianze, ai fini della
hanno congruenti: [FC] = [BC], [EF] = [AB], e B
dimostrazione, interessa la prima: [FC] = [BC].
Per l’ipotesi 8 si ha che [BC] = [CM], allora per la proprietà transitiva si deduce che [FC] = [CM].
Da questa uguaglianza scaturisce che il parallelogrammo ed il rettangolo hanno basi uguali ([FC] =
[CM]).
Per il rettangolo R, se la base è il segmento [CM], allora l’altezza è il segmento [CH].
Per il parallelogrammo P, se la base è il segmento [CF], allora, per le stesse considerazioni svolte
nella prima parte della dimostrazione, l’altezza è il segmento [CH].
In conclusione, il parallelogrammo P ed il rettangolo R hanno la stessa altezza [CH] ed hanno due
basi congruenti, [FC] = [CM], pertanto sono equivalenti (P  R)
Terza parte
Riunendo le conclusioni delle due parti si ha:
Q  P (quadrato equivalente al parallelogrammo)
R  P (rettangolo equivalente al parallelogrammo)
per la proprietà transitiva si ha
R  P (rettangolo equivalente al quadrato)
Questa conclusione non è altro ciò che si voleva dimostrare (c.v.d.).
La versione algebrica del primo teorema di Euclide è la seguente:
Indicando con c1 la lunghezza del cateto [AC], l’area del quadrato Q è
2
2
Area _ quadrato  c 1  AC 
Indicando con x e i rispettivamente i lati del rettangolo R, cioè:
x = [CH] = [MK]
i = [CM] = [HK] = [BC] = ipotenusa
2
Primo Teorema di Euclide
l’area del rettangolo, R, risulta:
Area rettangolo = xi
Dalla equivalenza del quadrato e del rettangolo si ha:
c1  x  i
2
Teorema di Pitagora
Una conseguenza del teorema di Euclide
è il teorema più noto della geometria
euclidea: il teorema di Pitagora.
Applicando il teorema di Euclide al
quadrato costruito sul cateto c1 si ottiene
che Q1, [ADEC], è equivalente al
rettangolo R1, [HCMK.]
Q1  R 1
ovvero:
2
c 1  i  [CM ]
Applicando lo stesso teorema al secondo
quadrato, Q2, costruito sul secondo cateto,
c2, si ottiene che il quadrato, [ABNS], è
equivalente al rettangolo R2, [BHKL],
cioè:
Q2  R 2
ovvero
2
c 2  i  [BH]
Sommando i due rettangoli, R1 e R2, si ottiene il quadrato [BCML]. Infatti essi in comune uno
stesso lato, [HK], che, per costruzione, è isometrico all’ipotenusa [BC]. Inoltre la somma degli altri
due lati, [CH] e [HB] non è altro che la ipotenusa [CB]. Pertanto il lato del quadrato [BCML] non è
altro che la ipotenusa del triangolo rettangolo [ABC].
Pertanto, per una proprietà delle figure equicomposte, si ha che il quadrato [BCML] è composta da
due rettangoli, [HCMK] e [BHKL], che sono, rispettivamente, equivalenti ai quadrati Q1, [ADEC],
e Q2, [ABNS]
BCML  Q1  Q2
Quindi: Il quadrato che viene costruito sulla ipotenusa di un triangolo rettangolo è equivalente
alla somma dei quadrati costruiti sui cateti (teorema di Pitagora).
3