Soluzioni del compito di Fisica Generale I del 28 gennaio 2016

FISICA GENERALE I
A.A. 2014-2015
28 Gennaio 2016
Cognome
Nome
Matricola
Corso di Studi
Docente
CFU
8-9
Ritirato
(barrare
e
firmare)
:
Voto:
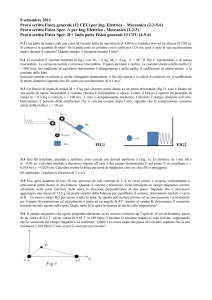
Esercizio n. 1 Una molla ideale di costante elastica k è posta su un piano
10
12
orizzontale privo di attrito e reca al suo estremo libero una massa m. A distanza
L/2 dalla posizione di equilibrio x0= 0 della massa è posta una parete (vedi figura),
Se la molla viene compressa di un tratto L a partire da x0 e poi lasciata libera, e i
successivi urti tra m e la parete sono elastici, determinare
a) l’impulso ceduto alla parete a ogni urto ; b) il tempo necessario perché m
compia una oscillazione completa.
Eseguire i calcoli per k= 4 N/m, m= 50 g, L= 10 cm.
Al momento dell’urto con la parete la velocità v* di m si ricava dalla conservazione dell’energia :
1
1 𝐿2 1
𝑚𝑣 ∗2 + 𝑘 = 𝑘𝐿2
2
2 4 2
𝑣∗ = √
→
3𝑘
𝑚
𝐿 = 0.77
4𝑚
𝑠
L’impulso trasferito in un urto vale quindi
𝐽 = 2𝑚𝑣 ∗ = 0.077 𝑁𝑠
A sinistra del punto di equilibrio si ha un normale moto armonico di periodo 𝑇 = 2𝜋√(𝑚/𝑘) = 0.7 𝑠 , mentre a destra il
moto è interrotto dalla parete. Ponendo t= 0 nel momento in cui la massa passa per la posizione di equilibrio si ha
𝑥(𝑡) = 𝐿 sin 𝜔𝑡
e quindi in ogni oscillazione l’urto contro la parete avverrà dopo un tempo t* dal passaggio dalla posizione di equilibrio
tale che
𝑥(𝑡 ∗ ) =
𝐿
2
→
𝐿 sin 𝜔𝑡 ∗ =
𝐿
2
→
𝑡∗ =
1
𝜔
sin−1
1
2
e il periodo complessivo del moto sarà:
𝑇=
𝑇0
2
+ 2𝑡 ∗ =
𝑇0
2
[1 +
2
𝜋
1
sin−1 ] = 0.47 𝑠
2
Esercizio n. 2 In un sistema di coordinate cartesiane Oxyz, il piano xy coincide con
il terreno orizzontale e l’asse z è verticale. Un corpo di massa M esplode da fermo,
quando si trova nel punto (0, 0, h), in 2 frammenti di masse m 1, m2. Subito dopo
l’esplosione entrambi i frammenti hanno velocità parallela al piano orizzontale e la
velocità del frammento m 1 è v1.
Determinare le coordinate di caduta di m 2.
Eseguire i calcoli per m 1= 6 kg, m2= 4 Kg, h= 100 m, v1= (-15 i + 20 j) m/s.
Dal momento dell’esplosione a quello dell’impatto (contemporaneo) a terra dei 2 frammenti le coordinate x e y del
centro di massa, inizialmente nulle, non variano.
Le coordinate dei punti di impatto dei 2 frammenti devono quindi soddisfare le relazioni
𝑚1 𝑥1 + 𝑚2 𝑥2 = 0
;
𝑚1 𝑦1 + 𝑚2 𝑦2 = 0
Ma le coordinate di caduta di m1 si possono calcolate dal tempo di caduta t*=(2h/g)1/2= 4.52 s:
𝑥1 = 𝑣1𝑥 𝑡 ∗
;
𝑦1 = 𝑣1𝑦 𝑡 ∗
Sostituendo :
−𝑚1 𝑥1
−𝑚1 𝑣1𝑥 𝑡 ∗
=
= 101.7 𝑚
𝑚2
𝑚2
−𝑚1 𝑣1𝑦 𝑡 ∗
−𝑚1 𝑦1
𝑦2 =
=
= −135.6 𝑚
𝑚2
𝑚2
𝑥2 =
Esercizio n. 3 Un’asta di lunghezza L può ruotare senza attrito attorno ad un
asse orizzontale passante per un suo estremo O. L’asta ha densità lineare di massa
λ(x)= bx2, dove x è la distanza da O e b è una costante. Al centro dell’asta è fissata
una molla ideale di costante elastica k, il cui altro estremo è vincolato al soffitto S
(vedi figura). La lunghezza di riposo L0 della molla è proprio uguale alla distanza
verticale tra il soffitto e O.
Sapendo che la sbarretta è in equilibrio quando è inclinata di un angolo θ0 rispetto
alla verticale, e che in tale situazione la molla è disposta in verticale (vedi figura),
determinare il valore di b.
Eseguire i calcoli per k= 20 N/m, L= 1 m, θ0= 30°.
All’equilibrio il momento totale rispetto ad O della forza peso e della forza elastica deve essere nullo.
Quando l’inclinazione è θ0 la molla è deformata di (L/2)cosθ0 e la forza è applicata al centro dell’asta. La forza peso è
invece applicata nel centro di massa, a distanza rc da O. Allora
𝐿
𝐿
𝑘 𝑐𝑜𝑠𝜃0 𝑠𝑖𝑛𝜃0 − 𝑚𝑔𝑟𝑐 𝑠𝑖𝑛𝜃0 = 0
2
2
→
𝑘
𝐿2
𝑐𝑜𝑠𝜃0 = 𝑚𝑔𝑟𝑐
4
𝐿
𝐿
Ma per definizione di centro di massa : 𝑚𝑟𝑐 = ∫0 𝑥𝜆(𝑥)𝑑𝑥 = ∫0 𝑥 𝑏𝑥 2 𝑑𝑥 = 𝑏
e sostituendo
𝑘
𝐿2
𝐿4
𝑐𝑜𝑠𝜃0 = 𝑔𝑏
4
4
→
𝑏=
𝐿4
4
𝑘
𝑐𝑜𝑠𝜃0 = 1.77 𝑘𝑔/𝑚3
𝑔𝐿2
Esercizio n. 4 Un numero n di moli di un gas biatomico è contenuto in un recipiente
cilindrico chiuso da un pistone libero di muoversi senza attrito e sottoposto alla pressione
atmosferica p0. All’equilibrio iniziale il volume è V0 (vedi figura). Al tempo t= 0 e per un
tempo t* si trasferisce calore al gas con una potenza W e di conseguenza il gas si espande
lentamente fino ad un nuovo stato di equilibrio. Determinare i valori di p, V, T in questo
nuovo stato.
Il gas viene poi compresso isotermicamente in modo reversibile fino a ritornare al valore di
entropia iniziale. Determinare il volume finale Vf del gas.
Eseguire i calcoli per n= 2, V0=50 lt, W= 5 W, t*= 10 minuti.
Nello stato iniziale T0= p0V0/nR= 304 K
La prima trasformazione èuna isobara reversibile in cui il gas riceve una quantità di calore Q= Wt*= ncpΔT e compie
un lavoro L=p0ΔV= nRΔT.
Allora
∆𝑇 =
𝑄
𝑊𝑡 ∗
=
𝑛𝑐𝑝
𝑛𝑐𝑝
→
𝑇 = 𝑇0 +
𝑊𝑡 ∗
= 356 𝐾
𝑛𝑐𝑝
; 𝑝 = 𝑝0
; 𝑉 = 𝑉0 +
𝑛𝑅∆𝑇
𝑊𝑡 ∗ 𝑅
= 𝑉0 +
= 0.058 𝑚3
𝑝0
𝑐𝑝 𝑝0
La seconda trasformazione è una compressione isoterma reversibile, e si vuole che la variazione totale di entropia sia
nulla, ossia
0 = ∆𝑆 = ∆𝑆𝑖𝑠𝑜𝑏 + ∆𝑆𝑖𝑠𝑜𝑡 = 𝑛𝑐𝑝 𝑙𝑛
𝑉𝑓
𝑇
+ 𝑛𝑅 𝑙𝑛
𝑇0
𝑉
→
𝑙𝑛
𝑉𝑓
𝑐𝑝
𝑇0
=
𝑙𝑛
𝑉
𝑅
𝑇
da cui
𝑇0 𝑐𝑝 /𝑅
𝑉𝑓 = 𝑉 ( )
= 0.033 𝑚3
𝑇
In alternativa gli stati iniziale e finale devono essere collegati da una adiabatica reversibile :
𝑇
1/(𝛾−1)
𝑉𝑓 = 𝑉0 ( 0)
𝑇
= 0.033 𝑚3