Scheda 1: PENDENZA

Scheda 1: PENDENZA
1. La prima riga della tabella qui sotto illustra il significato del segnale di salita ripida e pendenza.
Completa la seconda riga per illustrare la pendenza del 10%.
Pendenza del 20% Pendenza del 10% 2. Leggi il seguente problema.
Secondo il codice della strada il segnale di salita ripida preavverte di un tratto di strada con
pendenza tale da costituire pericolo. Si sta realizzando una strada rettilinea che, con un
percorso di 1,2 km, supera un dislivello di 85m.
a. Qual è la percentuale da riportare sul segnale?
b. Qual è l’inclinazione α (in gradi sessagesimali)?
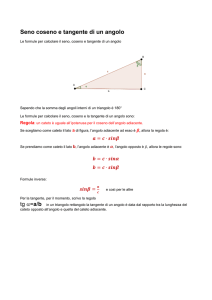
3. Completa il procedimento qui sotto con l’aiuto del tascabile per rispondere al quesito a.
Fig.1
BC
La percentuale deve indicare la pendenza m, che, in questo problema è data da m =
AB
È dato il dislivello BC lungo ………………, ma non conosco AB.
Per trovare AB applico al triangolo ABC, rettangolo in B, il teorema di ……………....... e scrivo:
AB = ………………………………………………......
€
E quindi
........
m≅
≅ ........... ≅ .....%
..........................................................
4. Spiega perché non puoi risolvere il quesito b applicando il teorema di Pitagora.
________________________________________________________________________________
€
5. Nel file ‘pendenza1.ggb’ è riprodotta in scala la figura 1. Apri il file, fai variare BC, completa la
tabella qui sotto e rispondi alle domande seguenti
α
BC
m
0,85
1,7
8,5
c. Qual è la l’inclinazione richiesta nel quesito b del problema? ……………………
d. Spiega perché m è direttamente proporzionale a BC.
e. Spiega perché α non è direttamente proporzionale a BC.
________________________________________________________________________________
________________________________________________________________________________
Anna Maria Miele, Treccani Scuola
1
6. Il software mostra la misura dell’inclinazione α, ma non mostra il procedimento seguito. Il file
‘pendenza2.ggb’ esplora le relazioni fra lati e angoli di un triangolo rettangolo per scoprire il
procedimento. Apri il file, fai variare il punto C e rispondi alle seguenti domande:
• Mentre C scivola lungo la semiretta AE, varia l’angolo α? ……..
BC BC AB
• Spiega perché variano i lati AB, AC e BC, ma restano costanti i tre rapporti
,
,
AB AC AC
___________________________________________________________________________
7. Muovi il punto rosso in basso per variare la lunghezza h, così puoi variare l’angolo α. Fissa, ad
€ che i tre rapporti
esempio, h = 2 e, successivamente, fai variare C come prima. Troverai
dipendono soltanto dall’angolo α; per questo in matematica si dà un nome a questi tre rapporti.
BC cateto opposto ad α
AB cateto adiacente ad α
AC ipotenusa
8. Completa il seguente procedimento per calcolare seno, coseno e tangente di 30°, 60° e 45°.
sin 30° =
.....
.....
cos30° =
.....
.....
sin 45° =
.....
.....
cos45° =
.....
.....
sin60° =
......
......
cos60° =
.....
.....
.....
.....
.....
tan60° =
tan45° =
.....
.....
.....
9. Per altri angoli non ci sono procedimenti geometrici elementari per determinare seno, coseno e
tangente, perciò bisogna usare il tascabile scientifico, che darà risultati approssimati. Usate la
calcolatrice scientifica tascabile
per completare la seguente
€ tabella e attenzione!
€
• Controllate che la calcolatrice sia predisposta per valutare gli angoli in gradi.
• Scrivete i valori di sinα, cosα e tanα arrotondati con due cifre dopo la virgola e i valori degli
angoli arrotondati al grado.
Angolo α sinα Sequenza di tasti
cosα
Sequenza di tasti tanα Sequenza di tasti
10°
80°
45°
30°
0,25
0,25
0,25
0,85
0,85
0,85
10
10
10
tan30° =
€
10. Perché si riesce a trovare l’angolo che ha per tangente 10, ma non l’angolo che ha 10 per seno o
per coseno?
________________________________________________________________________________
________________________________________________________________________________
Anna Maria Miele, Treccani Scuola
2