13-Fratture e Vene

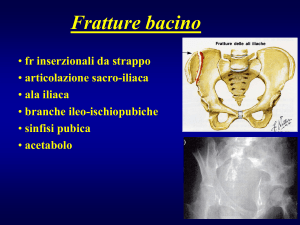
PARTE 7: FRATTURE E VENE
Le fratture (o joint) sono tra le strutture più importanti nel campo dell’idrogeologia, della
geologia mineraria e ingegneristica e nella geologia degli idrocarburi.
Lo sviluppo di fratture è essenzialmente legato a tre processi:
•Deformazioni risultanti da processi orogenici;
•Deformazioni risultanti da processi epeirogenici;
•“sfaldamento” causato da raffreddamento o disseccazione
Le fratture si possono formare durante l’intera storia di una roccia, partendo dalla diagenesi,
passando per il seppellimento, fino all’esumazione e il raggiungimento della superficie
terrestre dove, ad esempio, fenomeni di weatering possono produrre fratturazione. Quindi è
molto importante stabilire la corrispondenza tra fratture e loro ambiente di formazione e
quindi filtrare i dati in modo tale da analizzare solo quelli utili.
La maggior parte delle fratture (forse >95%) che si formano nelle rocce sedimentarie è più o
meno perpendicolare alla stratificazione. Le fratture possono mostrare un andamento planare
(systematic fractures), oppure avere un profilo curvilineo (non-systematic fractures). Quando
più fratture sono parallele tra loro allora formano un set di fratture (più set tra loro
geneticamente legati formano un sistema o array). Generalmente fratture non planari sono
associate al weatering o all’azione antropica (vedi le fratture radiali causate dagli esplosivi
nelle cave).
Sistemi di fratture
Joint arrays
Cooling joints: form by thermal contraction
Exfoliation joints: Form by unloading of bedrock through erosion.
They form parallel to topography
Exfoliation joints: Form by unloading of bedrock through erosion.
They form parallel to topography
Tectonic joints: Form by tectonic stresses as opposed to
stresses induced by topography.
Secondo Griggs & Handin (1960) le fratture sono superfici lungo le quali il materiale soggetto ad
uno stress perde coesione e, a differenza delle faglie, le fratture non mostrano una dislocazione
da taglio ma invece possono mostrare una dislocazione tensile, tuttavia questa classificazione è
molto dipendente dalla scala di osservazione. Ad occhio nudo possiamo non apprezzare una
dislocazione da taglio che potrebbe essere vista invece con l’aiuto di un microscopio. Questa
dicotomia non tiene conto delle fratture “ibride” cioè quelle che mostrano entrambi le
dislocazioni.
Per giungere ad una corretta classificazione consideriamo i criteri di rottura che producono le
fratture e le faglie in termini di stress crostali e pressione dei fluidi:
A: fratture tensili (s3<0 e t=0)
B: fratture ibride (s3<0 e t>0)
C: faglie (s3>0 e t>0)
Lungo le fratture in realtà non c’è perdita totale
della coesione, in realtà la migliore definizione
sarebbe: un piano di debolezza che si forma in
un materiale sottoposto ad un campo di stress
Il concetto di perdita di coesione dipende anche dalla scala di osservazione e dal
processo deformativo che agisce. In realtà non c’è una separazione netta tra
deformazione fragile e duttile.
a,b: deformazione fragile
c: deformazione fragile-duttile
d: deformazione duttile
strain
Joints/Fractures: Kinematics
ribs are arrest lines- opening is
not instantaneous, but rhythmic,
like splitting wood
Plumose structure: A
subtle roughness on
surface of some joints;
resembles imprint of a
feather. Due to
inhomogeneity of rock.
Close-up views of
hackles in plumose
structure. Plumose
structure is more
prominent away from
origin due to stress
concentrations at
crack tips
Joints: commonly
elliptical
Le fratture si sviluppano nelle rocce in tempi
diversi e per diverse ragioni
Classificazione delle fratture: criteri
•Presenza o assenza di riempimento (vene, filoni, dicchi...)
•Interazione tra fratture di set differenti (cronologia delle fratture)
•Morfologia
•Aspect ratio (rapporto di forma)
•spaziatura e relazione con la stratificazione
Morfologia e ambiente di formazione
A volte dalla morfologia è possibile risalire all’ambiente di sviluppo, per esempio se riusciamo a
identificare il tipo di farttura se fragile, semigrafile o duttile. La deformazione duttile in genere
avviene a grandi profondità (passaggio duttile-fragile localizzato all’isoterma 250-300°C quindi
considerando un gradiente termico normale di 30°C/km è posto a 10 km) oppure quando la roccia
non era consolidata. Mentre la deformazione fragile avviene in condizioni più superficiali e quando
la roccia è “abbastanza” litificata.
Indice di scabrosità: profili e pettine di Barton
Aspect ratio
i)
ii)
iii)
iv)
v)
Strutture tensili
Extension gash
Vena
Vena
Vena sottile o joint riempito
Joint
Attenzione: l’apertura delle fratture può
essere aumentata dal weatering
atmosferico!!
i) Fault
ii) Faglia minore
iii) Faglia minore o shear joint
maggiore
iv) Shear joint
v) Shear joint
Strutture da taglio
Le fratture possono essere classificate anche in base alla loro lunghezza rispetto
allo spessore dello strato (in rocce sedimentarie stratificate)
Le fratture stratabound sono quelle
fratture che terminano lungo i giunti di
stratificazione
Le fratture non-stratabound sono quelle
che o sono più corte o più lunghe dello
spessore dello strato
Problema: quale spessore usare?
Lo strato meccanico è inteso come la
porzione di roccia che si comporta in
maniera omogenea ad una
sollecitazione, cioè la porzione di
roccia con lo stesso comportamento
reologico (stratigrafia meccanica)
Ulteriori caratteristiche che definiscono le fratture:
•Apertura
•Lunghezza
•Spaziatura (densità)
•Orientazione (set, sistemi)
L= lunghezza
A= apertura
S=spaziatura
1/S= densità di fratturazione (per unità di
misura)
Le fratture stratabound mostrano una relazione con lo spessore dello strato dove si
sviluppano:
C’è una relazione diretta tra spaziatura e spessore o inversa tra densità e spessore,
quindi più gli strati sono sottili e più sono fratturati, viceversa più sono spessi e
meno sono fratturati
Tuttavia per spessori maggiori di
1-2 metri la legge non è più
lineare ma tende ad essere
asintotica verso un valore
costante.
Parametri che controllano la densità
di fratturazione
•Composizione
•Granulometria
•Porosità
•Spessore degli strati
•Posizione strutturale
COMPOSIZIONE
In generale rocce formate da
minerali a comportamento
fragile mostreranno una densità
di fratturazione maggiore
rispetto a quelle formate invece
da minerali a comportamento
duttile (nelle stesse condizioni a
contorno es P, T, Fluidi...).
Generalmente la dolomia è più
fragile rispetto al calcare...
Oppure più minerali fragili (es.
Quarzo, feldspato, dolomite) più
diventa resistente e più si
frattura!
POROSITA’
Più le rocce sono porose e più
decresce la resistenza (la
relazione non è lineare)
In generale rocce poco porose
(a parità di litologia e fabric)
sono più fratturate rispetto a
rocce molto porose.
GRANULOMETRIA
In rocce clastiche ben classate,
la decrescita della granulometria
corrisponde ad una crescita
della resistenza tensile. Questa
crescita è causata da una
crescita nell’energia di superficie
mentre diminuisce il diametro
dei granuli.
Quindi rocce più fini sono più
fratturate di rocce più
grossolane.
POSIZIONE STRUTTURALE
Con l’aumentare dello strain aumenta
la densità di fratturazione.
Come facciamo a prevedere la
densità di fratturazione conoscendo la
forma della struttura?
Il primo metodo è usare una
modellizazione ad elementi finiti, il
secondo è conoscere il raggio di
curvatura della struttura (esempio una
piega)
Quanto più è piccolo il raggio di curvatura tanto più aumenta la densità di
fratturazione e dove più velocemente varia il dip della struttura più la roccia è
fratturata.
Scan line – Scan area
Il campionamento statistico consiste nella rilevazione delle caratteristiche di un
insieme di fratture che siano rappresentative delle strutture presenti nell’area in
studio. Il campione può essere costituito dalle fratture che intersecano una
superficie, solitamente contenuta nel paino campagna o in affioramento (scan area),
oppure che intersecano una retta ideale, opportunamente orientata, sul piano
dell’affioramento (scan line).
Micro scan line
Scan line e micro scan lines
La modalità di esecuzione
della scan line – in termini
di orientazione,
lunghezza, caratteristiche
delle fratture che vengono
registrate ecc. , dipende
dalle caratteristiche dei set
di fratture che si
analizzano e dagli scopi
dell’analisi statistica. In
ogni caso la giacitura delle
fratture è uno dei
parametri che viene
sempre registrato,
nell’esecuzione di scan
line.
1 mm
100 m
Scan line condotte a varie scale di osservazione
500 m
Analisi delle giaciture
La prima fase dell’analisi strutturale
consiste nell’individuazione delle
principali famiglie di fratture. Una
prima distinzione spesso può già
essere effettuata dall’osservazione
in campagna. Tuttavia un’opportuna
analisi statistica è necessaria,
poiché fornisce informazioni
quantitative circa la giacitura media
dei set di fratture ed in molti casi
consente di osservare caratteristiche
relative a tali set, che non sempre
possono essere osservate tramite
un’analisi visiva, quali ad esempio,
la dispersione delle giaciture rispetto
alla giacitura media, la presenza di
sub-set di fratture ecc.
Set 2
Set 1
Set 2
Bed 56
Bed 1
Set 2
Set 2
Set 1
Set 1
Bed 71
Bed 66
Set 1
Set 2
Set 2
Bed 107
Bed 102
Set 2
Bed 118
Set 1
Set 2
Bed 120
Set di fratture da trazione rilevate in una successione
carbonatica. Poli dei piani di frattura su proiezione
stereografica equivalente – emisfero inferiore.
Fractures per meter
Distribuzione spaziale e trend delle
densità di fratture
Vertical
set
Shear fractures - vertical set local fracture density
150
100
50
0
0
200
400
600
800
1000
Distance (cm)
Orthogonal
to bedding
plane set
1200
1400
1600
1800
Diagramma del trend delle
densità di fratture locali
lungo la scan line, relativo
alle fratture sub-verticali
(vertical set)
Distribuzione statistica degli attributi delle fratture
All lithologies
1,2
Cumulative
F teor -- FDistribution
osserv
La distribuzione statistica di una
variabile continua X è comunemente
descritta tramite la funzione di
distribuzione cumulativa F(x).
Questa è definita come la
probabilità che X < x. La
distribuzione cumulativa empirica,
su un campione di N elementi, è
calcolata come numero di elementi
per i quali risulti X < x, rapportato al
numero totale N. Si noti che risulta
F(x) ≤ 1 per ogni valore di x, ed è
sempre crescente. Talvolta si
considera la probabilità che X > x. In
tal caso le proprietà della funzione
distribuzione non cambiano, eccetto
il fatto che essa è sempre
decrescente.
1
0,8
0,6
0,4
0,2
0
1
10
100
spessore(cm)
Bed Thickness
Distribuzione di frequenza
cumulativa degli spessori degli
strati di una successione
carbonatica.
1000
Distribuzione statistica degli attributi delle fratture
Bed 56 - set 1
10000
-1
Cumulative
Frequency
(m-1)(m
Frequency
Cumulative
)
Alcune distribuzioni statistiche
possono presentare frequenze
infinite. Tali distribuzioni non
possono essere descritte da una
funzione per la quale risulti F(x) ≤
1 per ogni valore di x.
In questi casi introduce una
analoga funzione, la frequenza
cumulativa, definita come numero
di elementi per i quali risulti X > x,
per unità di lunghezza (o di
superficie nel caso della scan
area).
Microscope
1000
Pro scope
Outcrop
100
Power Law
10
y = 8,8697x -0,9052
1
0,001
0,01
0,1
1
10
0,1
Aperture (mm)
Frequenza cumulativa delle aperture di
joint appartenenti ad un set di fratture
rilevato in una successione carbonatica. Il
modello di distribuzione statistica che
meglio si adatta a questi dati è una legge
di potenza di eq. y = 8.87 x-0.9 (riportata in
fig.). Si noti che, secondo questo modello,
le frequenze possono assumere valori
infiniti. Ad esempio il numero di fratture per
metro per le quali risulti: 0 < apertura <
0.001 , tende (teoricamente) ad infinito.
Distribuzioni di frequenze e di
frequenze cumulative
0.4
Frequenze
0.35
0.3
0.25
0.2
0.15
0.1
0.05
0
50
55
60
65
70
75
80
85
90
95
100
105
110
Peso (kg)
1.2
Frequenza Cumulativa
Le distribuzioni statistiche di variabili
aleatorie continue (per es. il peso di
individui maschi di una certa
popolazione umana) sono spesso
rappresentate in termini di frequenze,
ossia numero di individui appartenenti
ad una certa classe di peso (per es.
75 – 80 kg), oppure di frequenze
cumulative, ossia numero di individui
con peso inferiore ad un certo valore.
Si noti che l’ordinata di ogni punto del
diagramma di frequenze cumulative è
pari alla somma dei valori di
frequenza (non cumulativa) alla
sinistra dell’ascissa. Per es. la
frequenza cumulativa relativa al peso
di 75 kg è data dalla somma delle
aree dei rettangoli alla sinistra del
valore 75.
1
0.8
0.6
0.4
0.2
0
45
55
65
75
85
95
105
115
Peso (kg)
Frequenze e frequenze cumulative del peso di individui maschi
di una certa popolazione. Le distribuzioni sono ben
approssimate da una distribuzione di Gauss, la quale presenta
tipicamente la forma a ‘campana’ per le frequenze e la forma
ad ‘S’ per le frequenze cumulative.
Distribuzioni statistiche più comuni
Frequenza
Frequenza Cumulativa
Due tipi di distribuzione molto frequentemente incontrati in natura sono la
distribuzione di Gauss - o Normale – e la distribuzione secondo una legge di
potenza, ossia descritta da un’equazione del tipo: F(x) = a x –m , dove a ed m sono
costanti. Si noti che questa equazione fornisce una retta in un diagramma bilogaritmico.
Un esempio tipico di distribuzione Normale è fornito dal peso di individui di una
certa specie.
Un esempio di distribuzione simile alla legge di potenza può essere fornito dal
peso degli individui quando si considerano tutte le specie animali. In questo caso
le frequenze relative alle
classi di peso più piccole (per esempio quando si
Gauss
Distribuzione unicellulari),
di frequenza Normale o di
considera il numero dei piccoli insetti, oppure degli organismi
Gauss. La forma a campana indica che al
assumono valori indefinitamente grandi.
valore medio è associata la massima
frequenza (ossia
la legge
massimadi
probabilità),
Si noti infine nel caso della distribuzione cumulativa secondo
una
mentre i valori più distanti dalla media sono
potenza, anche la distribuzione di frequenza (non cumulativa)
è descritta da una
via via meno probabili.
legge di potenza, fornita dalla derivata di F(x).
Power law
Distribuzione di frequenza secondo una
x
20
18
16
14
12
10
8
6
4
2
0
0
1
2
3
x
4
5
6
Frequenza Cumulativa
Frequenza
x
20
18
16
14
12
10
8
6
4
2
0
0
2
4
x
6
8
10
legge di potenza. I valori più piccoli della
variabile x assumono frequenze
indefinitamente grandi. La media di questa
distribuzione può assumere solo valori: 0 ed
∞. Pertanto tale distribuzione non ammette
media né deviazione standard.
0, 5
1,2
0, 45
1
Frequenza
Frequenza
Cumulativa
Altre distribuzioni frequentemente incontrate
Un altro tipo di distribuzione
frequentemente incontrato in
geologia strutturale è la
distribuzione Log Normale. Una
variabile aleatoria il cui logaritmo
ha distribuzione Normale è per
Spessore (cm)
spessore
definizione Log Normale.
Grandezze come la spaziatura o
lunghezza delle fratture possono
presentare questa distribuzione.
Se nel diagramma delle
frequenze si utilizza la scala
logaritmica per le ascisse (ossia
spessore
Spessore
si considera il logaritmo della
variabile analizzata), la
Distribuzioni statistiche degli spessori degli strati in una successione
carbonatica. Nei diagrammi in basso le ascisse sono in scala
frequenza e la distribuzione
logaritmica. Si noti come, in quest’ultimo caso, le distribuzioni
cumulativa assumono la forma assumano la tipica forma Gaussiana.
tipica - a campana ed a S
rispettivamente – della
distribuzione Gaussiana.
0,8
0,6
0,4
0,2
0
0, 3
0, 25
0, 2
0, 15
0, 1
0, 05
0
0
50
100
150
200
250
0
1,2
50
100
150
200
250
300
350
0, 5
0, 45
1
Frequenza
Frequenza
Cumulativa
0, 4
0, 35
0,8
0,6
0,4
0,2
0, 4
0, 35
0, 3
0, 25
0, 2
0, 15
0, 1
0, 05
0
0
1
10
100
1000
1
10
100
1000
Altre distribuzioni frequentemente incontrate
1 - Cumulative distribution
La distribuzione esponenziale descrive il tempo
intercorso tra due eventi con distribuzione
temporale random. Per esempio il tempo che
Exponential
intercorre tra il passaggio di un’auto e la
successiva ad un casello autostradale (nell’ipotesi
y = 1.1234e
R = 0.9807
di assenza di code).
Analogamente, nel caso di una scan line, una
distribuzione spaziale random delle fratture dà
luogo ad una distribuzione esponenziale della
distanza tra una frattura e la successiva.
spacing (mm)
L’equazione che descrive tale distribuzione è:
y = 1.1234e-1.9018x
10
F(x) = 1 -  e -  , dove  è l’inverso del valor
R2 = 0.9807
medio.
1
0
0.5
1
1.5
2
2.5
Per comodità di rappresentazione nei diagrammi
0.1
a lato è riportata la funzione 1 – F(x).
Una peculiarità di questa distribuzione sta nel
0.01
fatto che per essa la media e la deviazione
spacing (mm)
standard assumono lo stesso valore.
Frequenze cumulative della spaziatura tra joint in una sezione
Un metodo pratico per riconoscere tale
sottile di calcare micritico, con ordinate in scala lineare e
distribuzione consiste proprio nel calcolare il
logaritmica. Usando la scala logaritmica, la distribuzione
rapporto tra deviazione standard e media, per
cumulativa esponenziale è descritta da una retta.
verificare se si approssimi all’unità. Tuttavia è
sempre consigliabile lo studio dei diagrammi della
distribuzione cumulativa, come quelli affianco
riportati.
1.2
-1.9018x
1
2
0.8
0.6
0.4
0.2
0
1 - Cumulative distribution
0
0.5
1
1.5
2
2.5
Scopi dell’analisi statistica
La descrizione di oggetti naturali caratterizzati da una geometria marcatamente irregolare, quali le rocce e le
strutture in esse contenute, può essere realizzata efficacemente tramite un approccio statistico.
Per esempio, per descrivere la geometria di un oggetto artificiale come un pilastro di cemento armato, basta
rappresentarne la forma, le tre dimensioni, la distanza tra un’armatura ed un’altra ecc. Nel caso di una roccia
fratturata, una descrizione geometrica non può essere attuata in maniera così semplice. L’approccio statistico
fornisce utili strumenti per la sua descrizione.
Le caratteristiche di maggior interesse per le quali è utile una descrizione in termini statistici, sono le seguenti:
lunghezza della traccia delle fratture sul piano dell’affioramento
spaziatura tra fratture
apertura dei joint da trazione o slip delle fratture da taglio
Se di ognuna di tali caratteristiche se ne fornisce
a) Il corretto modello di distribuzione statistica (per es. gaussiana, esponenziale
o legge di potenza ecc.)
b) I parametri che definiscono tali modelli (per es. la media e deviazione
standard oppure l’esponente ed il coefficiente della legge di potenza ecc.)
allora la descrizione delle strutture può essere ritenuta esaustiva ai fini applicativi. Queste grandezze sono di notevole
interesse perché controllano il comportamento meccanico ed idraulico (in termini di porosità e permeabilità) dell’ammasso
roccioso.
Fasi dell’analisi statistica
Determinazione del modello di distribuzione statistica
Parametri statistici come la media o la deviazione standard non sono sufficienti a descrivere le caratteristiche delle
fratture se non si conosce a monte il tipo di distribuzione. Per esempio, nel caso di una variabile Log Normale
oppure esponenziale la media differisce notevolmente dal valore più probabile, dato dalla massima frequenza (non
cumulativa). Nel caso della legge di potenza è addirittura inappropriato riferirsi alla media, poiché essa non assume
valori finiti non nulli.
Per la determinazione del corretto modello statistico esistono svariati metodi più o meno sofisticati. Un criterio
piuttosto semplice (anche se non infallibile) consiste nell’analisi dei diagrammi della distribuzione cumulativa,
analoghi a quelli presentati negli esempi precedenti. Il confronto delle distribuzioni osservate con quelle teoriche,
secondo vari metodi di best-fit, può fornire utili informazioni circa la distribuzione statistica della grandezza
studiata.
Determinazione dei parametri statistici che definiscono le distribuzioni
Una volta determinato il modello statistico appropriato, la distribuzione può essere completamente definita
determinandone gli opportuni parametri statistici. Per esempio, una volta noto che un certo attributo (per es. la spaziatura)
segue una distribuzione di Gauss, è sufficiente determinarne la media e la deviazione standard. Tali valori si inseriscono
poi nell’equazione della distribuzione di Gauss, ottenendo una formulazione completa della distribuzione di probabilità
della grandezza studiata. Nel caso della distribuzione esponenziale è sufficiente stimare la media (poiché nella relativa
equazione compare solo tale parametro). Nel caso della legge di potenza, invece, i parametri da determinare sono
l’esponente ed il coefficiente. Questi possono essere stimati tramite il metodo dei minimi quadrati, così come fatto negli
esempi precedenti.
I modelli di distribuzione di probabilità più ricorrenti
In letteratura sono citati svariati modelli, più o meno complessi, per descrivere gli attributi delle fratture.
Di seguito si riportano i più semplici e ricorrenti, per le principali caratteristiche.
Apertura delle fratture da trazione
Per tale attributo il modello più citato e documentato in letteratura è la LEGGE DI POTENZA. Secondariamente:
distribuzione LOG NORMALE.
Shear dispalcement delle fratture da taglio
Modelli più diffusi: LOG NORMALE, LEGGE DI POTENZA.
Lunghezza delle fratture
Modelli più diffusi: LOG NORMALE, LEGGE DI POTENZA.
Spaziatura tra fratture
Modelli più diffusi:
ESPONENZIALE: se le fratture hanno distribuzione spaziale casuale uniforme, ossia non sono equi-spaziate, non
sono raggruppate in zone di intensa fratturazione alternate a zone poco fratturate.
LOG NORMALE
LEGGE DI POTENZA: questa distribuzione è appropriata nei casi in cui le fratture sono marcatamente
raggruppate. Per esempio le fratture fault related, presentano spaziature ridottissime nelle zone di faglia,
intervallate da regioni di roccia poco fratturate in cui le spaziature presentano valori elevati.
VENE
Vene
-forma dei cristalli presenti nelle vene:
Cristalli fibrosi:

Alto rapporto tra lunghezza
e spessore (>10 ... >100)

La forma fibrosa non è
determinata dall’habitus
del cristallo

La forma fibrosa è
indipendente
dall’orientazione
cristallografica

La forma di tutti I cristalli
è identica

Le fibre sono parallele

Nessuna nucleazione
durante la crescita
(Antitaxial calcite vein in carbonaceous shales,
Arkaroola, South Australia)
(Antitaxial calcite vein
in carbonaceous
shales, Arkaroola,
South Australia)
NB. Una tessitura fibrosa può essere formata da sub-granuli fibrosi o geminati, mentre I
granuli grandi possono non essere fibrosi. In questa foto si può osservare una sezione
perpendicolare alle fibre in una vena antitassiale. Un solo granulo ricopre la maggior
parte del campo. Le fibre sono molto più piccole e sono definite da sub-granuli e
probabilmente dai margini dei geminati.
Cristalli a blocchi
allungati:
(Syntaxial/asymmetric quartz vein from Cape
Liptrap, Victoria, Australia)
•Da basso ad alto rapporto tra
lunghezza e spessore(<10)
•La forma allungata non dipende
dall’habitus
•La forma allungata è spesso
legata all’orientazione
cristallografica
•Non tutti i cristalli presentano la
stessa forma
•Gli assi lunghi dei granuli sono
generalmente sub-paralleli
•Nessuna nucleazione durante la
crescita
A blocchi:
Nessuna
caratteristica
descritta per I
cristalli fibrosi o
allungati, in
particolare:
(Calcite vein in carbonaceous shales, Arkaroola,
South Australia)
•Spesso la
nucleazione è
continua
•Nessuna forma
allungata o
isorientazione dei
cristalli
Slicken-fibres:
•Fibrosi o a blocchi
allungati
•Asse lungo dei
cristalli a basso angolo
o parallelo ai margini
delle vene
(Calcite vein in carbonaceous shales, Arkaroola, South
Australia)
Tettonica e Geologia strutturale (2008-2009): Session 8-Vene
Classificazione in base al sito di precipitazione durante lo sviluppo della vena
Vene sintassiali:
•la crescita avviene persistentemente lungo lo stesso piano
•la crescita avviene nella zona centrale della vena
•La crescita spesso inizia con la sovracrescita sintassiale (con lo stesso senso
cristallografico) dei granuli della roccia incassante
•spesso sono a forma di blocchi allungati
•La parte più vecchia della vena si trova lungo i margini al contatto tra la vena e la roccia
incassante; la parte più giovane si trova nella parte mediana
•Singoli cristalli non attraversano il piano mediale
Vene antitassiali:
•la crescita avviene persistentemente lungo lo stesso piano
•La crescita avviene lungo i bordi
•I minerali che formano le vene sono spesso assenti nella roccia incassante
•I cristalli sono spesso fibrosi
•I cristalli più giovani si trovano ai bordi, i più vecchi nella parte centrale
•Singoli cristalli possono attraversare la parte mediana della vena.
Tips of two parallel en échelon antitaxial fibrous calcite veins. Mean fibre width increases slightly from the
median line outwards, which indicates that growth was outwards (antitaxial). Fibre shape is symmetric
around the median line, except near the tips. Growth and propagation of the veins caused bending if the
shale "bridge" in between. Tapley Hill Formation, Opaminda Creek, Arkaroola, South Australia. Width of view
13 mm, crossed polars.
Median zone in a dominantly fibrous antitaxial calcite vein. The median zone has an elongate blocky texture with growth
mainly from the right to the left. Small wall rock inclusions and quartz crystals mark the edge of the median zone. Antitaxial
growth took place after formation of the median zone, with fibres growing out of median zone grains. The fibre width is
much smaller than the grain size in the median zone, but comparable in size to the deformation twins in these grains. This
indicates that the initial (median zone) vein was deformed before the onset of fibre growth. Tapley Hill Formation,
Opaminda Creek, Arkaroola, South Australia. Width of view 6.4 mm, crossed polars.
Vene atassiali o stretching veins:
•La crescita avviene in vari siti (cracks) nel tempo
•I cristalli spesso sono i principali minerali della roccia
incassante
•Cristalli stirati
•non c’è una ripartizione consistente tra cristalli vecchi e
nuovi
•non c’è un piano mediano
•singoli cristalli possono estendersi da una parte all’altra della
vena
I Cracks possono avvenire dentro la vena o in modo casuale
all’esterno (ma sempre paralleli alla vena). In questo caso la
vena contiene molti pezzi della roccia incassante.
Vene asimmetriche:
•La crescita inizia in modo atassiale (ma può essere anche
sintassiale o antitassiale)
•Un lato della vena diventa il piano preferenziale di
crescita
•Spesso sono blocchi allungati
•Le vene sono asimmetriche
Vene da rimpiazzamento:
•I cristalli non precipitano in nuovi spazi ma rimpiazzano
minerali preesistenti.
•Generalmente i bordi sono imprecisi
•Spesso restano le inclusioni dei minerali precedenti
•La forma è spesso a blocchi allungati o influenzata dalla
precedente tessitura
Vene composite:
•Combinazione di crescita antitassiale
nel centro e crescita sintassiale ai
bordi.
•Generalmente le parti sintassiale e
antitassiale sono composte da diversi
minerali
(Calcite + quartz vein in carbonaceous
shales from Arkaroola, South
Australia)
(Calcite + quartz vein in carbonaceous shales from
Arkaroola, South Australia)
a
b
Photomicrograph of a polytextured,
fibrous and blocky calcite vein in (a)
plane polarised light and (b) cross
polarised light. The initial veins is
marked by a thin line of wall rock
inclusions (S) and a line of quartz
crystals (Q). Subsequently, two stages of
vein growth occurred: (1) antitaxial
fibrous growth towards the left and (2)
open cavity growth on the right. The
cavity infill took place by overgrowth of
the first vein material (at line Q), but
also by nucleation and growth of new
crystals, resulting in a dominantly
blocky texture. Infill of the cavity was
not complete as cavities with faceted
grain surfaces remained (C). This
indicates that the blocky growth was
probably the last growth event, postdating leftward antitaxial fibrous growth
from line S (right half of vein not
shown). Width of view 10 mm.
(Stylolite in calcite vein in carbonaceous shales
from Arkaroola, South Australia)
stiloliti:
Le stiloliti sono in un certo senso
opposte alle vene (quindi è spesso
usato il termine anti-crack).
•Dissoluzione continua e ripetitiva
lungo una superficie
•Accumulo di materiale insolubile
(spesso scuro o opaco) lungo la stilolite
•Sviluppo di denti di sega dovuto alle
diverse velocità di dissoluzione su
entrambi I lati della stilolite
•I dentelli indicano la direzione del
raccorciamento
Stylolite and quartz vein combination in Heavitree Quartzite (Ormiston Gorge, Central Australia).
A distinct stylolite dips shallowly to the right and truncates milky white vertical quartz veins. The
jagged surface of the stylolite, common in limestones but relatively rare in quartzites, indicates
vertical shortening, consistent with the horizontal stretching that is indicated by the quartz
veins. Scale bar is 1 cm. Photograph courtesy Alice Post.
Traiettorie di apertura
La traiettoria di apertura è il percorso che due punti, originariamente adiacenti, posti sui margini opposti di
una vena hanno effettuato muovendosi l’uno rispetto all’altro mentre la vena cresce.
Le fibre e i blocchi allungati spesso tracciano questa traiettoria ma non sempre in modo completo.
Le fibre fantasma possono qualche volta dare un’indicazione più precisa della traiettoria rispetto alle fibre
normali. Le fibre fantasma sono le tracce di un minerale diverso che cresce da un punto specifico sui bordi.
Vene e analisi strutturale
L’estesa varietà di strutture interne alle vene, la forma e l’arrangiamento spaziale, fanno delle vene uno
strumento molto utile per l’analisi strutturale. Spesso I cristalli a blocchi allungati o quelli fibrosi ci
permettono di determinare l’intera storia della formazione della vena dando informazioni sulla storia
deformativa della roccia incassante. Le microstrutture dovrebbero essere interpretate correttamnente (sin o
antitassiali, tracciamento parziale o totale…)
Le vene formano spesso dei sistemi. L’immagine a
fianco mostra un gruppo di vene formatesi
originariamente con un piccolo angolo con
l’orizzontale. L’interazione tra le vene ha causato
la loro fusione in un’unica vena orizzontale con
pezzi di roccia inclusi. L’immagine a destra mostra
invece un set di vene sigmoidali. Le vene non si
sono formate tutte nello stesso istante ma in
diversi stadi deformativi. Le vene sigmoidali sono
spesso degli ottimi indicatori cinematici.
Vene sigmoidali
•L’apertura di una vena corrisponde alla massima estensione
istantanea.
•La traiettoria di apertura registra la cinematica della
deformazione.
•La propagazione dei tip della vena è parallela alla direzione di
max raccorciamento istantaneo.
•L’apertura delle vene è parallela al max allungamento
istantaneo.
•Le vene ruotano quando la deformazione non è coassiale o
quando c’è una rotazione del campo deformativo.
Che tipo di vena è? Sintassiale, antitassiale , atassiale, composita…
Che tipo di vena è? Sintassiale, antitassiale , atassiale, composita…
Strain/pressure fringes & shadows intorno ad oggetti rigidi
Un oggetto rigido come un cristallo di pirite disturba il campo di stress o deformativo intorno ad
esso durante la deformazione. Sui lati dell’oggetto normali alla massima compressione, lo stress
differenziale e la pressione sono i più alti (aree di max strain).
Mentre sui lati normali alla minima compressione lo stress differenziale e la pressione sono i più
bassi (aree di basso strain).
La differenza di pressione può portare al trasporto di materiale formando delle ombre di
pressione o frange di pressione.
Pressure fringe of fibrous quartz
around a concretion of iron ore in
a BIF-chert from the Hamersley
ore province, Pilbara, West
Australia.
Width of view 2.3 mm, crossed
polars.
Quartz + mica pressure shadow
adjacent to a quartz porphyroclast (on
right, grey grain with inclusions) in a
quartz-mica schist from
Nooldoonooldoona Waterhole, S.W.
Mount Painter Inlier, Arkaroola, South
Australia. Width of view 3.2 mm,
crossed polars. Note the sharp
boundary of the pressure fringe, in
contrast to the vague boundary of the
pressure shadow
OMBRE versus FRANGE
Precipitazione distribuita in aree di bassa
pressione:
pressure shadow (ombre di pressione)

Generalmente tessitura a blocchi

Margini mal-definiti delle ombre

Simili alle vene di rimpiazzamento
Precipitazione localizzata in aree di bassa
pressione:
pressure fringe (frange di pressione)

Generalmente tessitura fibrosa o a blocchi
allungati

Margini ben definiti delle frange

Simili alle vene sin/anti-tassiali e composite
NOTA: la ricristallizazzione tardiva può produrre una tessitura a blocchi in una frangia di pressione
rendendola simile ad un ombra di pressione.
The crack-seal mechanism
The crack-seal mechanism (Ramsay 1980) is the favoured mechanism for about all veins with elongate
crystals. In this model growth occurs in many repeated small increments: crack-seal events:
•Crack event -> opening of narrow open crack, filled with fluid
•Seal event -> Precipitation fills (=seals) the crack again
Most telling microstructural indicators of crack-seal mechanism are regularly spaced trails of small
inclusions (typically small micas or pieces of wall rock or fluid inclusions). Opening per crack event is
generally in the order of 10 m.
Elongate blocky and stretching textures are very well explained by, and often show evidence of crack-seal
growth (inclusions, radiator structures)
- Crack-seal mechanism, pressure and fluid flow
The crack-seal cycle involves the
buildup of fluid pressure to enable
fracturing (Crack). Then increased
permeability allows fluid flow and
material transport (Seal) and the fluid
pressure drops.
•Presence of cracks -> fluid can flow
through crack network
•Presence of cracks -> brittle failure
(often extensional)
Extensional failure -> high fluid
pressure & low differential stress
Mohr failure envelope representation (after Lockner
1995) in a graph of the shear stress (t) against
principal normal stresses (s1 and s3, with the rock
pressure Pr = (s1+s3)/2). The Mohr-circle is a circle
with its centre on the horizontal axis. Points on the
circle represent normal stress / shear stress
conditions on all possible planes. The angle b is the
angle between the failure surface and the direction
of maximum principle stress (s1). (a) When the
Mohr-circle does not touch the Mohr-envelope,
stresses are too low to induce failure. (b) Fluid
pressure (Pf) reduces the effective pressure, which
moves the Mohr circle to the left. Fluid pressure can
rise until the Mohr-circle touches the Mohr envelope,
at which point failure occurs. In the given case, with
Pf>s3, failure is tensile (b=0°). (c) Shear failure
(b=40°) can occur at relatively lower fluid pressure,
but at a higher differential stress. (d) Tensile strength
of an existing fracture is close to zero, which shifts
the Mohr-envelope down. Less differential stress
and fluid pressure is needed to reactivate such an
existing fracture.
Fibrous antitaxial calcite veins in carbonaceous shales. The veins form fracture-like sets
with side splays where the interaction between two veins caused a local disturbance of
the stress field. Tapley Hill Formation, Opaminda Creek, Arkaroola, South Australia.
Set of sigmoidal en échelon veins that
have amalgamated into a single dextral
shear vein. Heavitree Quartzite, Ormiston
Gorge, Central Australia. Photograph
courtesy Alice Post.
Photograph looking down on slickenfibres
in Heavitree Quartzite (Ormiston Gorge,
Central Australia). diameter 1 A$ coin
approx. 2 cm. Photograph courtesy Alice
Post.
Breccia or net veins form a matrix between
clasts in a breccia. These typically occur in
hydrothermal (ore) deposits. True breccia
veins formed in one event of extensive
fracturing, without significant preferred
orientation. However, abundant veining of
other types and/or the activity of multiple
veining events with different cross-cutting
orientations may produce breccia-like veins
(Valenta et al. 1994).