GREGORIO MENDEL
1822- 1884
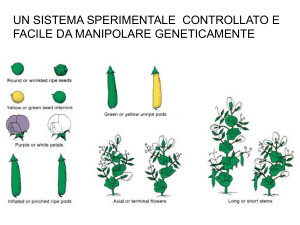
UN SISTEMA SPERIMENTALE CONTROLLATO E
FACILE DA MANIPOLARE GENETICAMENTE
STRUTTURA DEL FIORE
UN SISTEMA SPERIMENTALE CONTROLLATO E
FACILE DA MANIPOLARE GENETICAMENTE
ISOLAMENTO DI LINEE PURE
MANIPOLAZIONE DEI
FIORI PER EVITARE
L’AUTOFECONDAZIONE
Esperimento ripetuto
invertendo il sesso delle
piante
RISULTATI DEGLI ESPERIMENTI OTTENUTI INCROCIANDO
PIANTE CHE DIFFERISCONO PER UN SOLO CARATTERE
Linee pure
F1
F2
Rapp. F2
1.
semi lisci
X
rugosi
Tutti lisci
5474 lisci; 1850 rugosi
2,96:1
2.
semi gialli X
verdi
Tutti gialli
6022 gialli; 2001 verdi
3,01:1
3.
petali rossi
Tutti rossi
705 rossi; 224 bianchi
3,15:1
4.
fiori terminali X assiali
Tutti assiali
651 assiali;207 terminali
2,95:1
5.
baccelli sempl. X concamer.
Tutti semplici
882 semplici; 299 concam. 2,82:1
6.
baccelli verdi X gialli
Tutti verdi
428 verdi; 152 gialli
3,14:1
7.
steli lunghi
Tutti lunghi
787 lunghi; 277 corti
2,84:1
X
bianchi
X corti
Nella F1 il carattere che viene espresso è detto dominante, l’altro
recessivo.
Nella F2 piante con carattere dominante : piante carattere recessivo = 3:1
LE OSSERVAZIONI DI MENDEL
GLI IBRIDI F1 ESPRIMONO SOLO IL CARATTERE
DOMINANTE
NELLA GENERAZIONE F2 COMPAIONO PIANTE SIA CON IL
CARATTERE RECESSIVO CHE CON IL CARATTERE
DOMINANTE
NELLA GENERAZIONE F2 LE PIANTE CON CARATTERE
DOMINANTE SONO IL TRIPLO DI QUELLE CON
CARATTERE RECESSIVO
IL MODELLO DI MENDEL
PER CIASCUN CARATTERE UN ORGANISMO POSSIEDE
DUE DETERMINANTI CHE POSSONO ESSERE NELLA
FORMA DOMINANTE O RECESSIVA
NELLA FORMAZIONE DEI GAMETI UNO SOLTANTO DEI DUE
DETERMINANTI VIENE SEGREGATO CON UGUALE
PROBABILITA’
IL GAMETE MASCHILE FECONDA IL GAMETE FEMMINILE
FORMANDO UNO ZIGOTE CON DUE DETERMINANTI PER
CIASCUN CARATTERE
IL MODELLO SPIEGA I RISULTATI SPERIMENTALI
IL MODELLO PREDICE CHE INCROCIANDO UN
IBRIDO DI PRIMA GENERAZIONE CON UN
OMOZIGOTE RECESSIVO SI DEVE OTTENERE
PER IL 50% UN FENOTIPO DOMINANTE E PER IL
RIMANENTE 50% UN FENOTIPO RECESSIVO
PRIMA LEGGE DI MENDEL
I DUE MEMBRI DI UNA COPPIA DI DETERMINANTI
(ALLELI) SI SEPARANO L’UNO DALL’ALTRO
DURANTE LA FORMAZIONE DEI GAMETI
Fenotipi liscio e rugoso
SECONDA LEGGE DI MENDEL
DURANTE LA FORMAZIONE DEI GAMETI LA
SEGREGAZIONE DI UNA COPPIA DI ALLELI DI UN
GENE È INDIPENDENTE DALLA SEGREGAZIONE
DEGLI ALLELI DI UN ALTRO GENE
MEIOSI
PROBABILITA’ E STATISTICA
Applicazioni delle leggi di Mendel per predire il risultato degli incroci genetici
Con che probabilità si ottiene un certo tipo di progenie?
Per questi calcoli si utilizzano 3 regole matematiche:
Regola della somma
Regola del prodotto
Espansione binomiale
Metodi statistici per valutare se i dati osservati negli incroci siano in
accordo con gli attesi: Metodo del chi quadrato
Regola del prodotto: usata per prevedere la probabilità di eventi indipendenti.
P che si verifichi l’evento E1 al primo lancio e la probabilità che si verifichi l’evento E2
al secondo lancio
P (E1, E2) = P(E1) x P(E2)
Regola del prodotto: usata per prevedere la probabilità di eventi indipendenti
P (E1, E2) = P(E1) x P(E2)
g = recessivo = verde
G = Dominante = giallo
GG x gg
F1
Gg x Gg
F2
GG, Gg, gg
1 2
1
3/4
1/4
La generazione F2 era composta per 3/4 da piante con piselli gialli e
per 1/4 da piante con piselli verdi
Qual è la probabilità di osservare 3 piante con semi verdi?
(1/4)3 = 1/64 = 0,016
Regola della somma: usata per prevedere la probabilità di eventi mutualmente
esclusivi.
P di ottenere con un lancio l’evento E1 oppure l’evento E2
P (E1 oppure E2) = P(E1) + P(E2)
Regola della somma: usata per prevedere la probabilità di eventi mutualmente
esclusivi
P (E1 oppure E2) = P(E1) + P(E2)
Esempio:
gameti
GgLl x GgLl
GL
Gialli Gg
Rugosi Ll
gL
gl
GL GGLL GGLl GgLL GgLl
gameti
Qual è la probabilità di ottenere
progenie con semi gialli e rugosi,
semi gialli e lisci, e semi verdi e
rugosi?
Gl
Gl
GGLl GGll GgLl Ggll
gL GgLL GgLl ggLL ggLl
gl GgLl Ggll
ggLl ggll
9: 3:
3: 1
9/16 + 3/16 + 3/16 = 15/16 o 0,94 = 94%
9/16
3/16
3/16
1/16
La distribuzione binomiale
Quando si fa uso della probabilità bisogna rendersi conto che vi sono modi
diversi in cui una serie di eventi può manifestarsi
Esempio: matrimonio tra due genitori eterozigoti (Aa) per l’albinismo
P che il figlio abbia normale pigmentazione = ¾ (¼ AA + ½ Aa)
P che il figlio sia albino = ¼ (aa)
Quale è la probabilità di generare 3 figli tutti albini?
¼ x ¼ x ¼ = 1/64
Quale è la probabilità di 3 figli dei quali 1 albino e 2 con pigmentazione normale?
Probabilità di varie serie di eventi:
1° A, 2°N, 3°N = ¼ x ¾ x ¾ = 9/64
1° N, 2°A, 3°N = ¾ x ¼ x ¾ = 9/64
1° N, 2°N, 3°A = ¾ x ¾ x ¼ = 9/64
Regola della somma: 9/64 + 9/64 + 9/64 = 27/64
La distribuzione binomiale
Come si fa a calcolare le probabilità quando le combinazioni possibili aumentano?
Per esempio: nel caso di 5 figli dei quali 2 affetti da albinismo e 3 con pigmentazione
normale?
Oppure:
Qual è la proporzione di famiglie con 5 figli composte da 3 maschi e 2 femmine ?
PER CALCOLARE LA PROBABILITA’ BISOGNA APPLICARE LA
DISTRIBUZIONE BINOMIALE
La distribuzione binomiale
Qual è la proporzione di famiglie con 5 figli composte da 3 maschi e 2 femmine (3M + 2F)
trascurando l’ordine di nascita, cioè MMMFF e MFMFM sono equivalenti
a = Probabilità che nasca un maschio = (M) = ½
b = Probabilità che nasca una femmina = (F) = ½
n = numero totale di termini = 5
La binomiale per questa situazione è: (a + b)n = (a + b)5
L’espansione ci dice la frequenza (probabilità) di ogni tipo di campione di una data
dimensione (trascurando l’ordine di comparsa)
MMMMM; MMMMF; MMMFF; MMFFF; MFFFF; FFFFF
Il triangolo di Pascal dà i coefficienti che precedono ciascun termine dell’espansione per
n grandi
(a + b)5 = a5 + 5a4b + 10 a3b2 + 10a2b3 + 5ab4 + b5
1 MMMMM; 5 MMMMF; 10 MMMFF 10 MMFFF; 5 MFFFF; 1 FFFFF
10 a3b2 = 10 x (1/2)5 = 10/32 = 5/16
Triangolo di Pascal
n
1
2
3
4
5
6
1
1
1
4
1
1
5
6
2
3
3
1
1
6
1
1
4
10 10
5
15 20 15 6
1
1
1
Ogni termine del triangolo è la somma dei due numeri che stanno immediatamente
sopra a destra e a sinistra
Dal triangolo di Pascal (1 MMMMM; 5 MMMMF; 10 MMMFF 10 MMFFF; 5
MFFFF; 1 FFFFF)
( a + b)5 = a5 + 5a4b + 10 a3b2 + 10a2b3 + 5ab4 + b5
10 a3b2 = 10 x (1/2)5 = 10/32 = 5/16
La distribuzione binomiale
Metodo alternativo consiste nell’uso della formula binomiale per la quale in “n tentativi”
binomiali la probabilità che un evento si verifichi s volte e l’evento alternativo t volte è data
da:
P=
n!
------ x as bt
s! t!
Se a = ½ b = ½; n = 5; s = 3; t = 2;
P=
5!
------ x a3 b2
3! 2!
5x4x3x2x1
--------------------------- x (1/2)3 x (1/2)2 = 10 x (1/2)5 = 5/16
(3 x 2 x1) x (2 x 1)
La distribuzione binomiale
Caso 3 geni con 2 possibili alleli alternativi: A/a, B/b C/c, un dominante (D) o un recessivo (r)
Locus
Locus
Locus
Frequenza
A/a
B/b
C/c
1/8
D
D
D
1/8
D
D
r
1/8
D
r
D
1/8
r
D
D
1/8
D
r
r
1/8
r
D
r
1/8
r
r
D
1/8
r
r
r
Espansione di una espressione binomiale: descrizione matematica di un procedimento di
campionamento nel caso di 2 sole alternative. L’espansione ci dice la frequenza
(probabilità) di ogni tipo di campione di una data dimensione. Abbiamo fatto una
espansione di (a + b)n dove
a = p (allele dominante in un locus) = D = ½
Con che probabilità un gamete avrà 2
b = p (allele recessivo in un locus) = r = ½
alleli dominanti e 1 recessivo?
n = numero di coppie geniche = 3
P = (a + b)3
Triangolo di Pascal dà i coefficienti che precedono ciascun termine dell’espansione per n grandi
P = 1 a3 + 3a2b1 + 3ab2 + 1b3
La probabilità che un gamete contenga 3D
= 1/8
2D, 1r = 3 x (1/2) 2 x (1/2) = 3/8
2r , 1D = 3/8
3r
= 1/8
Metodo alternativo consiste nell’uso della formula binomiale per la quale in “n tentativi”
binomiali la probabilità che un evento si verifichi s volte e l’evento alternativo t volte è data
da:
n!
------ x a3 b1
s! t!
Dove s + t = 1 a = ½ b = ½ n = 3
3x2x1
------------ x (1/2)2 x (1/2)1 = 3 x (1/2)3 = 3/8
(2 x1) x1