IL PROBLEMA:
Per produrre un bene un’ industria sostiene costi
fissi settimanali di 4000 € , costo per unità
prodotta di 80€; il prezzo di vendita è di 160
€ per ogni unità.
Settimanalmente non si possono produrre più di
100 unità.
Determina la funzione costo, la funzione ricavo,
rappresentale sul piano cartesiano e calcola il
BEP commentando il risultato.
I DATI DEL PROBLEMA:
costi fissi settimanali : 4000 €
costo per unità prodotta :80€
prezzo di vendita per unità: 160 €
IN QUESTO CASO SIETE FORTUNATI!!
I DATI SONO NEL TESTO DEL PROBLEMA…
QUANDO SARETE DEI MANAGER LI DOVRETE TROVARE
VOI!!!!!!
ANALISI DEI DATI
Individuiamo le variabili:
variabile indipendente (x): quantità prodotta e
venduta
variabile dipendente (y): costo totale
( y=C ); ricavo (y = R)
Individuiamo i vincoli:
la quantità prodotta/venduta è non negativa
la quantità prodotta/venduta non può superare
le 100 unità settimanali
ANALISI DEI DATI
Individuiamo le relazioni fra le grandezze:
Costo totale = Costi fissi + Costi variabili
Ricavo = prezzo unitario * quantità
BEP = punto di incontro fra costi e ricavi
ANALISI DEI DATI
SINTESI
modello matematico
Utilizziamo e formalizziamo le relazioni
individuate in precedenza:
Costo totale : C(x) = 4000+ 80x
Ricavo: R(x) = 160x
vincoli :
o≤x≤1000
RISOLUZIONE :
Algebrica :
Risolviamo il sistema
Grafica:
Visualizziamo i grafici
delle funzioni
y 4000 80 x
y 160 x
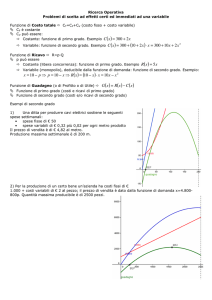
RISOLUZIONE GRAFICA
Commento:
Se 0<x<50
costi >ricavo
Se x=50
costi = ricavo
BEP = (50,8000)
Se 50<x<100
costi < ricavo
grafico delle funzioni costo e ricavo
18000
16000
14000
12000
10000
Costi
Ricavo
8000
6000
4000
2000
0
0
50
100
FASI PER RISOLVERE UN PROBLEMA:
Raccolta dati
Analisi
Sintesi: modello matematico
Risoluzione
Verifica dei risultati