angoli e bisettrici

ANGOLI E BISETTRICI
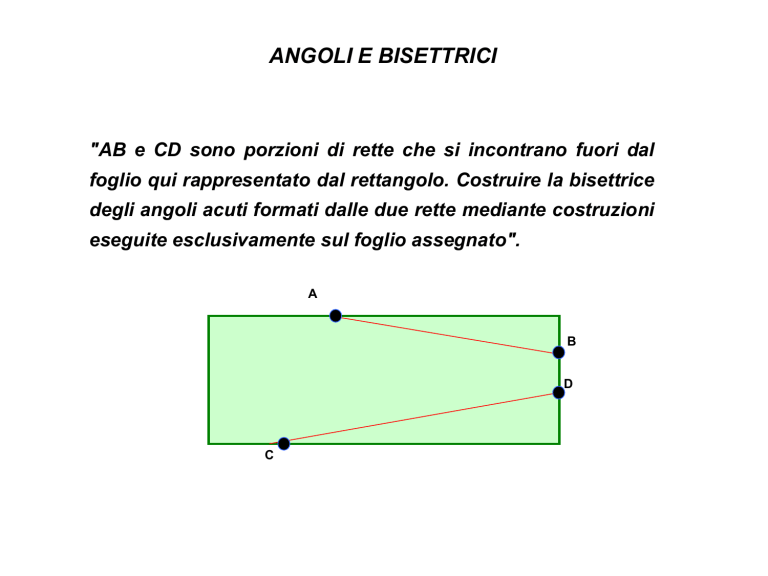
"AB e CD sono porzioni di rette che si incontrano fuori dal
foglio qui rappresentato dal rettangolo. Costruire la bisettrice
degli angoli acuti formati dalle due rette mediante costruzioni
eseguite esclusivamente sul foglio assegnato".
A
B
D
C
FIGURE CONCAVE E CONVESSE
Definizione: Una figura F’ si dice convessa se, comunque si scelgano
due suoi punti, il segmento che li unisce è un sottoinsieme di F’.
B
D
E
A
C
F
Definizione: Una figura F’’ si dice concava se esistono almeno due suoi
punti tali che il segmento che li congiunge non è sottoinsieme di F’’.
Postulato: Ogni retta r suddivide il piano π in tre sottoinsiemi
disgiunti r, p’, p’’.
p’
 ' ' '  ?
 ' ' '  ?
B
A
C
r
p’’
D
π
I sottoinsiemi p’ e p’’ sono tali che un segmento AB i cui estremi
appartengono entrambi a p’ ( o entrambi a p’’) non ha alcun punto in
comune con r, mentre un segmento CD i cui estremi appartengono l’uno
a p’ e l’altro a p’’ ha un punto in comune con r.
Definizione: Con riferimento al precedente postulato, si dice semipiano di
origine r ciascuno dei due insiemi di punti
 '  p'r
e
 ' '  p' 'r
Due semipiani distinti, di comune origine, come π’ e π’’, si dicono opposti
Siano π’ e π’’ due semipiani aventi per origine le rette r’ e r’’.
1° Caso: π’ e π’’ hanno le origini incidenti in un punto O. Allora
 ' ' '
è detto angolo convesso. Il punto O si dice vertice dell’angolo, mentre le
semirette OA e OB si dicono lati dell’angolo
r’’
r’
π ’’
π’
O.
 ' ' '
 ' ' '

2° Caso: π’ e π’’ coincidono
è un angolo piatto
r’=r’’
A
O
.
B

3° Caso: π’ e π’’ sono semipiani opposti
è un angolo nullo o giro
'
r’=r’’
A
 ''
O
.
B
 ' ' '
4° Caso: Le origini r’ e r’’ di π’ e π’’ sono rette parallele e distinti. In
questa situazione la figura intersezione riveste interesse solo se π’
contiene r’’ e π’’ contiene r’

è una striscia
 ' ' '
'
r’’
 ' ' '
 ''
r’
Definizione: Sia dato un angolo AOB. La semiretta OM che divide
l'angolo nei due angoli uguali AOM e MOB dicesi bisettrice dell'angolo
AOB.
Scheda 1: Come risolveresti il seguente problema? Hai a
disposizione il software Cabrì o Geogebra.
AB e CD sono porzioni di rette che si incontrano fuori dal foglio qui
rappresentato dal rettangolo. Costruire la bisettrice degli angoli
acuti formati dalle due rette mediante costruzioni eseguite
esclusivamente sul foglio assegnato
A
B
D
C
Scheda 2: Costruisci la bisettrice di un angolo convesso, seguendo i
seguenti passi. Puoi far uso del software didattico Cabrì.
1. Disegna un angolo. Chiama O il vertice, a e c le due semirette.
2. Disegna una circonferenza f di centro O e raggio qualsiasi, chiama A e B i punti di
intersezione con le semirette a e c.
3. Disegna una circonferenza d di raggio qualsiasi e di centro A e chiama D il punto
di intersezione con la semiretta a.
4. Disegna una circonferenza e di centro B e raggio AD (basta trasportare il
segmento AD, raggio della circonferenza d, nel punto B e tracciare la circonferenza
richiesta)
5. Chiama C il punto di intersezione tra le due circonferenze d e e.
6. Traccia la semiretta b di origine O e passante per C. Essa costituisce la
bisettrice dell’angolo AOB.
7. Descrivi cosa accade al variare del raggio della circonferenza f .
………………………………………………………………………………………………
……
Scheda 3: Sulla base di quanto ottenuto
nella scheda precedente, segui i passi
seguenti. Puoi usare solo riga e compasso.
1.Definisci un punto qualunque sulla bisettrice ottenuta e chiamalo P.
2.Dal punto P traccia le perpendicolari ai due lati dell’angolo.
3.Determina l’intersezione fra le perpendicolari ed i lati dell’angolo e chiama i
punti, rispettivamente, V e Z.
4.Definisci i segmenti PV e PZ e determina la loro lunghezza.
5.Definisci una tabella a due colonne e riporta in esse, rispettivamente, le
misure di PV e PZ. Raccogli un certo numero di valori (basta far variare il
raggio della circonferenza f)
PV
PZ
6. Riflettendo su tali valori enuncia la proprietà che caratterizza tutti e soli i
punti della bisettrice di un angolo e scrivila come commento al disegno.
…………………………………………………………………………………………
…………
Dimostrazione:
•CA=CB perché raggi di circonferenze uguali.
•OC in comune
•OA=OB perché raggi della stessa circonferenza.
I due triangoli sono quindi uguali per il 3° criterio di uguaglianza dei triangoli quindi
anche gli angoli sono uguali.
Luogo geometrico: Si chiama luogo geometrico una figura per la quale sia
stata enunciata una proprietà di cui godono tutti i suoi punti ed essi soltanto.
1.Ogni punto della figura possiede la proprietà prefissata
2.Un punto che gode di quelle proprietà appartiene alla figura
3.Un punto che non appartiene alla figura non possiede quella proprietà
Esempio:L’asse di un segmento è il luogo geometrico dei punti equidistanti
dagli estremi del segmento stesso
Scheda 4: Dimostra il seguente teorema.
Teorema: La bisettrice di un angolo è il luogo dei punti del piano equidistanti dai lati
dell'angolo.
Indica con PV e PZ le distanze del punto P della bisettrice dai lati dell'angolo.
Prima parte: P  bisettrice  PV=PZ
I triangoli OPV, OPZ hanno:
…………………………………………………………………………………………………
…………………………………………………………………………………………………
…………………………………………………………………………………………………
Quindi sono uguali per ........... criterio di uguaglianza dei triangoli.
Dimostrazione:
•OP in comune.
• Gli angoli VOP e POZ sono
uguali.
Per il secondo criterio generalizzato di
uguaglianza dei triangoli i triangoli sono
uguali
Seconda parte: PV=PZ  P bisettrice
Preso un qualunque punto P per il quale si abbia PV=PZ , devi dimostrare che
esso appartiene alla bisettrice. Traccia le distanze tra il punto P ed i lati
dell'angolo ed unisci P con il vertice O dell'angolo. Allora i triangoli OPV ed OPZ
hanno
………………………………………………………………………………………
…………
………………………………………………………………………………………
…………
………………………………………………………………………………………
…………
Concludi tu la dimostrazione
A
AB=DE D
AC=DF
Dimostrazione:
•OP in comune.
• PV=PZ.
G
B
C
E
F
GBC sono allineati, GAC è isoscele  AB è
anche mediana, pertanto BC=BG=EF.
Se i due triangoli hanno un cateto
e l’ipotenusa rispettivamente uguali 
Quindi i tre lati sono uguali e per il 3°
allora sono uguali.
criterio di uguaglianza sono uguali
Costruzione mediante segmenti, bisettrici, intersezioni,
adoperando la proprietà transitiva della congruenza.
1. Traccia due punti qualsiasi, P e Q, sui lati AB e CD, rispettivamente.
2. Congiungi P e Q.
3. Traccia le bisettrici degli angoli APQ e CQP.
4. Chiama S il punto di intersezione.
5. A questo punto traccia le bisettrici di BPQ e DQP e chiama R il punto di
intersezione.
Se consideri la retta passante per R ed S, avrai ottenuto la
bisettrice dell’angolo invisibile formato dai segmenti AB e CD?
Dimostralo, facendo le opportune congetture.
A
P
B
R
O
S
D
Q
C
(dimostrazione: il punto R, appartenendo alla bisettrice dell’angolo QPB è
equidistante dai lati PB e PQ; ma R appartiene anche alla bisettrice
dell’angolo DQP, quindi è equidistante dai lati PQ e QD; quindi, per la
proprietà transitiva della congruenza, R è equidistante dai lati PB e QD,
cioè dalle rette AB e CD: risulta pertanto sulla bisettrice richiesta.
Analogamente si dimostra che anche il punto S appartiene alla bisettrice
richiesta).
Scheda 5: Costruisci mediante segmenti, bisettrici, intersezioni e
adoperando la proprietà transitiva della congruenza la bisettrice dell’angolo
formato dai due segmenti AB e CD (vedi scheda 1) mediante costruzioni
eseguite esclusivamente sul foglio assegnato. Puoi far uso del software
didattico Cabrì.
1. Traccia le bisettrici degli angoli CAB e DCA , e chiama M il loro punto di
intersezione M.
2. Prendi un punto E su AB e un punto F su CD e traccia le bisettrici degli
angoli DFE e BEF.
3. Chiamo con N il loro punto d'intersezione.
Dimostra che i punti M ed N appartengono alla bisettrice dell'angolo avente
per lati AB e CD.
………………………………………………………………………………………
…………………
A
E
B
N
M
O
b
D
F
C
(dimostrazione: per definizione di bisettrice, M è equidistante dai lati AB e AC, perché
punto della bisettrice dell'angolo CAB, ma M è anche equidistante dai lati CD e AC,
perché punto della bisettrice dell'angolo DCA. Per la proprietà transitiva della
congruenza, M è equidistante sia da AB che da CD. N deve risultare interno al
rettangolo e questo dipende dalla scelta di E e di F. N è equidistante sia dal lato EB
che dal lato EF, perché punto della bisettrice dell'angolo BEF, ma N è anche
equidistante dai lati FD e EF, perché punto della bisettrice dell'angolo DFE.
Per la proprietà transitiva della congruenza, N è equidistante sia da EB che da FD,
quindi è equidistante da AB e CD. Poiché i punti M e N sono equidistanti dai segmenti
AB e CD sono punti della bisettrice dell’angolo di lati AB e CD).
Scheda 6: Costruisci adoperando circonferenze, rette parallele, rette
perpendicolari, intersezioni, proiezioni ortogonali, punti medi di segmenti, e i
teoremi di congruenza di angoli e di triangoli, la bisettrice dell’angolo formato
dai due segmenti AB e CD (vedi scheda 1) mediante costruzioni eseguite
esclusivamente sul foglio assegnato. Puoi far uso del software didattico Cabrì.
•Prendi a piacere due punti, P e P’, rispettivamente, sul segmento AB e sul segmento CD.
•Traccia le perpendicolari ai segmenti AB e CD passanti per i punti prescelti.
•Chiama con N un punto qualunque della perpendicolare ad AB, così puoi tracciare la
parallela al segmento AB passante per N e la circonferenza di centro P’ e raggio congruente a
PN.
Secondo te il punto N’ di intersezione tra la circonferenza costruita e la
perpendicolare a CD, risulta interno all’angolo determinato dalle rette AB e CD?
Giustifica la tua risposta.
………………………………………………………………………………………………
……
Disegna la parallela a CD passante per N’. Come puoi osservare, questa retta
interseca la parallela ad AB passante per N in un punto, che puoi chiamare V.
Denominando con T il punto di intersezione tra le due circonferenze di raggio RS e
centro, rispettivamente, R e S, dimostra la congruenza dei triangoli RTV e STV.
…………………………………………………………………………………………………
……
(dimostrazione: RV=VS per costruzione, in quanto raggi della stessa
circonferenza, RT=TS per costruzione, in quanto raggi di due circonferenze di
stesso raggio. Infine VT è in comune ai due triangoli. Pertanto, per il terzo criterio
di uguaglianza dei triangoli i due triangoli risultano uguali).
A
E
P
B
N
R
V
T
S
D
N'
P'
F
C
Secondo te quale caratteristica ha la retta passante per il segmento TV
……………………………………………………………………………………
...................................................................................................................
A
H
B
E
O
V
G
D
K
F
C
Congiungi i punti V ed O.
Cosa puoi dire sui segmenti EV, AB, FV e CD (per costruzione, EV risulta
parallelo ad AB, mentre FV risulta parallelo a CD)?
…………………………………………………………………………………………
………………
Indica con H e K i piedi delle perpendicolari condotte da V rispettivamente alla
retta AB e alla retta CD.
Secondo te, i segmenti VH e VK sono congruenti? Se pensi di sì, giustifica la tua
risposta.
…………………………………………………………………………………………….
Dimostra che i triangoli OVH e OVK sono congruenti tra loro.
………………………………………………………………………………………………
…………
(dimostrazione: per il quarto criterio di uguaglianza dei triangoli, due triangoli
rettangoli sono uguali se, oltre all’angolo retto, hanno ordinatamente uguali altri
due elementi, di cui almeno uno sia un lato. Nel nostro caso , VHO = VKO = 90°,
OV è in comune, VH = VK).
Secondo te la costruzione della bisettrice nel modo sopra esposto risulta ben
giustificata, ovvero puoi affermare che le bisettrici degli angoli AOC e EVF
coincidono? Motiva la tua risposta.
…………………………………………………………………………………………
………………
(dimostrazione: gli angoli HOV e KOV risultano congruenti e la retta OV è
bisettrice dell’angolo AOC. Tale retta è anche bisettrice di HVK, perché HVO =
KVO; inoltre, EVO = EVH + HVO =90° + HVO = 90° + KVO = KVF + KVO =
FVO, da cui si ricava che la retta OV è bisettrice dell’angolo EVF e, quindi, le
bisettrici degli angoli AOC e EVF coincidono tra loro).
A
P
B
Q
N
M
V
D
N'
P'
C
Secondo te, cosa accade al variare della scelta dei punti iniziali P e P’? E al
variare di N?
………………………………………………………………………………………………
…………