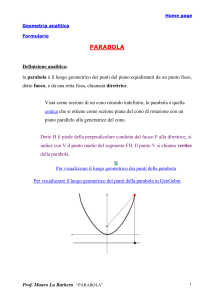
Parabola
Dato un punto F del piano
F
ed una retta d
si dice parabola l’insieme dei punti del piano
equidistanti dal punto F e dalla retta d
d
Parabola punto per punto
Ogni punto è
determinato
dall’eguaglianza
fra le distanze
punto-retta
punto-fuoco
fuoco F
direttrice
Per ogni punto il
valore delle
distanze(=raggio)
è diversa, tranne
che . . .
fuoco F
direttrice
L’insieme dei
punti (parabola)
• ha un punto particolare detto vertice
• è simmetrico rispetto alla linea asse di simmetria
Asse di
simmetria
F fuoco
V vertice
Rappresentazione della parabola nel piano cartesiano
10
Se nel piano
inseriamo un
sistema di assi
cartesiani si ha la
rappresentazione a
fianco della
parabola.
Il fuoco F e il
vertice V sono
punti,ognuno con le
sue coordinate,
l’asse di simmetria
è una retta
parallela all’asse
y.
8
6
F
4
V
2
4
2
0
2
4
2
4
6
8
10
I punti della parabola sono costruiti sull’eguaglianza delle
distanze dal fuoco e dalla direttrice
Variando fuoco e direttrice si possono ottenere parabole diverse
per posizione . . .
. . . e per ampiezza
I punti di una parabola
soddisfano tutti la
proprietà eguaglianza delle
distanze. Possiamo
determinarne l’equazione.
8
P
F
4
2
5
0
2
5
Cerchiamo l’equazione della parabola di fuoco
F(3 ,4 ) e direttrice d: y = 2 nel piano
cartesiano.
Per ogni punto P(x,y) della parabola si deve
ottenere :
distanza (P , F) = distanza ( P , retta d)
quindi
(x - 3) 2 + (y - 4) 2
= y -2
10
6
Esempio numerico
10
da cui
(x – 3)2 + ( y – 4)2 = (y –2)2
Sviluppando i calcoli si ottiene
x2 – 6x + 9 + y2 - 8y +16 = y2 – 4y + 4
e l’equazione della parabola :
y = 1/4 x2- 3/2
x +21/4
4
y = a x2
+b x
+c
Equazione generica della parabola
y ax2 bx c
a,b,c
R
Asse di simmetria parallelo asse y
x ay2 by c
a,b,c
R
Asse di simmetria parallelo asse x
Ci occuperemo qui delle parabole con asse di simmetria parallelo all’asse
y
Variazione dei grafici al variare dei coefficienti
y ax2 bx c
a,b,c
R
Vediamo come si presenta il grafico della parabola al variare dei valori
a,b,c
Con il pacchetto grafico che avete a disposizione disegnate nel piano
cartesiano le parabole :
Esercizio 1
y
2
x
y
y
2x 1
2
y
Esercizio 2
x
x
24
12
32 2
x
9
2
x
8x
1x
1x
24
12
2
1
25
3
x 4
y
y
18
32
9
2
x
160
3
1
x
192
Si ottengono i grafici
10
10
10
5
5
f( x)
g ( x)
h ( x)
10
10
5
0
5
5
0
5
10
5
5
10
Esercizio 1
Esercizio 2
10
10
10
x
a>0
10
Concavità
a<0
4
f( x )
0
4
4
x
4
10
Vertice
Esercizio 3
20
20
10
y
2
x
8 x 18f( x )
g( x )
y
2
x
8 x 18h( x )
20
10
0
10
20
p( x )
2
y
x
y
x
2
5 x 18
10
12 x 18
20
20
20
x
20
b
b 2 4ac
V(
,
)
2a
4a
50
Esercizio 4
y
2
x
40
8 x 20f( x )
20
g( x )
2
8 x 20
2
20
y
x
y
x
h( x )
20
20
10
0
10
20
20
20
Al variare di a e b
varia la posizione
dell’ascissa del
vertice, che ha
infatti coordinate :
x
20
Esercizio 5
2
y x 3x 2
2
y x 3x
2
y x 3x 2
Al variare di c varia la posizione del vertice per quanto riguarda
l’ordinata : il grafico della parabola risulta traslato
Intersezioni con gli assi
8
8
6
Esercizio 6
f( x)
2
y
0.25 x
y
0.25 x
y
0.25 x
2
2
4
2g (xx) 3
h ( x)
2
2x 4
2x 6
4
2
2
0
2
4
6
8
10
12
2
4
x
12
Quali sono i punti in cui la parabola taglia gli assi cartesiani ?
Per determinare il punto
d’intersezione con l’asse y si risolve il
sistema
y ax 2 bx c
x = 0
P(0,c)
Per determinare i punti d’intersezione
con l’asse x si risolve il sistema
y ax 2 bx c
Y = 0
Si ottiene un’equazione di 2°
grado in x
ax 2 bx c 0
le cui soluzioni rappresentano le
ascisse dei punti d’intersezione
La parabola ha due punti
d’intersezione con l’asse x
3
Se
b2-4ac>
0 f( x)
2
3
x
9
4
La parabola ha un punto
d’intersezione con l’asse x
Se b2-4ac= 0 f( x)
2
3
x
9
6
La parabola non ha punti
d’intersezione con l’asse x
Se b2-4ac< 0 f( x)
2
3
x
9
Inoltre
Se c=0
y=ax2+bx
4
La parabola passa per l’origine
f( x )
3
6
x
7
Se b=0
La parabola ha il vertice sull’asse y
y=ax2+c
Se b=0 e c=0
y=ax2
6
La parabola ha il vertice
nell’origine
f( x )
3
6
x
7
Formule
y=ax2+bx+c
vertice
10
b
b 2 4ac
V(
,
)
2a
4a
8
fuoco
6
F
4
V
2
4
2
0
2
4
2
4
6
8
10
b 1 (b 2 4ac )
F(
,
)
2a
4a
direttrice
1 (b 2 4ac )
d
4a
equazione asse di
b
x
simmetria
2a
Come si rappresenta la parabola di equazione y=ax2+bx+c nel
piano cartesiano
•Determinare le coordinate
del vertice V
4
•Determinare l’equazione
dell’ asse di simmetria
•Determinare le coordinate
degli eventuali punti
d’intersezione con gli assi
•Determinare le coordinate di
qualche altro punto, anche
tenendo presente la simmetria
•Rappresentare punti e asse
nel piano : essi
caratterizzano il grafico
2
2
0
2
2
4
V
4
Per farle a casa
Una torcia elettrica accesa
posta perpendicolarmente
ad una parete la illumina
formando un cerchio
Le coniche si
ottengono
intersecando
un cono ed
un piano : in
questo caso il
cono è il
fascio di luce
ed il piano è
la parete.
Se incliniamo la torcia si
ottiene un’altra figura
luminosa : l’ellisse.
Inclinando maggiormente la
torcia, la linea esterna
della parte illuminata
diventa una parabola
10
f( x)
4
Ruotando ancora di più si
ottiene un ramo di iperbole.
5
x
10