Lezione 3
( Capitolo 6 di DeLong)
Elementi costitutivi del
modello a prezzi flessibili
Il piano della lezione
• Il lato dell’offerta: (in particolare si parte dalla
produzione potenziale, flessibilità dei salari ed
equilibrio nel mercato del lavoro)
• Si introduce poi il lato della domanda: le
componenti della spesa interna e le loro
determinanti
• Infine per rendere il modello completo si
introduce il commercio internazionale
Macroeconomia neoclassica
(precedente al modello keynesiano)
Ipotesi:
• l’offerta determina la domanda
• vige un sistema di concorrenza perfetta
sui mercati
• i prezzi sono flessibili
• conta solo il sistema reale dell’economia
perfettamente : la moneta è solo un
lubrificante degli scambi
implicazioni del modello
le implicazioni che ne derivano sono quelle
definite classiche:
• piena flessibilità di prezzi e salari
• mercato del lavoro sempre in equilibrio
• produzione effettiva sempre uguale a quella
potenziale
• eventuali shock da domanda cambiano la
composizione del Pil ma non il suo livello
Dicotomia monetaria e reale
• La descrizione dell’economia reale nel
modello macroeconomico neoclassico si
fonda sulla legge di Say secondo la
quale: l’offerta crea la propria
domanda.
• La descrizione dell’economia
monetaria si fonda invece
sull’equazione degli scambi di Fisher
Legge di Say
• La produzione di beni e servizi nell’economia dipende dalla
produttività dei fattori e dall’offerta dei fattori di produzione
(lavoro, capitale).
• Il tasso di interesse (è un fenomeno reale) si aggiusta in
modo da mantenere in equilibrio il mercato dei fondi
prestabili.
• il salario reale si aggiusta in modo da garantire la piena
occupazione.
• Il livello di produzione, (l’offerta aggregata) pertanto, troverà
sempre una domanda equivalente. Qualsiasi squilibrio (eccesso
di domanda o di offerta)su qualsiasi mercato è sanato dai
meccanismi di mercato (prezzi, salari, tasso di interesse).
Dicotomia neoclassica
• Suddivisione delle variabili economiche
in due classi
• I settori monetario e reale sono separati
• L’equilibrio nel settore reale (mercato del
lavoro e mercato delle merci) determina il
livello del reddito reale
• il settore monetario (domanda e offerta
di moneta) determina soltanto il livello
generale dei prezzi e il tasso di inflazione
Differenze tra analisi classica ed analisi
keynesiana
Produzione potenziale, salari reali ed
equilibrio del mercato del lavoro
• Nel modello macroeconomico a prezzi
flessibili i due ingredienti fondamentali per
spiegare come si determina la produzione
potenziale e il livello dei salari reali sono:
• la funzione di produzione
• Il meccanismo di market clearing che opera
nel mercato del lavoro
La funzione di produzione
• Nella forma Cobb-Douglas della funzione di
produzione, come si è visto, l’output potenziale Y* è
dato dalla dotazione di lavoro L, dallo stock di
capitale K dell’economia, dall’efficienza del lavoro E
e dal parametro α che indica l’elasticità del prodotto
rispetto al capitale e la rapidità con cui operano i
rendimenti decrescenti del capitale. La funzione di
produzione assume cioè la forma:
Y* = K(LE)1-
La funzione di produzione
• Se la forza lavoro e l’efficienza
del lavoro sono mantenute
costanti, il PIL reale aumenta
all’aumentare dello stock di
capitale. Poiché ogni
successivo aumento dello
stock di capitale produce un
minore aumento del livello di
produzione, la funzione di
produzione è rappresentata da
una curva non rettilinea. Più
alto è il livello di , maggiore è
la curvatura e maggiore è la
rapidità con cui diminuiscono i
rendimenti dell’investimento.
Produzione potenziale, salari reali ed
equilibrio del mercato del lavoro
• Quando il sistema economico opera in condizioni di pieno
impiego, la produzione effettiva è uguale a quella potenziale
(ossia vi è il pieno utilizzo della capacità produttiva
dell’economia).
• Il meccanismo di market clearing che opera nel mercato del
lavoro, basato sull’ipotesi classica di flessibilità di prezzi e
salari, garantisce l’equilibrio tra domanda e offerta nel mercato
del lavoro e la piena occupazione.
• In equilibrio, ogni persona che desideri lavorare al salario
corrente (quello di market clearing) può farlo e ogni impresa
che intenda assumere lavoratori al salario corrente (quello di
market clearing) può farlo.
La domanda di lavoro
• Il primo passo per vedere come si stabilisce l’equilibrio nel
mercato del lavoro è determinare la domanda di lavoro.
Partiamo dalle seguenti ipotesi di concorrenza perfetta:
• nel sistema economico operano K imprese identiche, ognuna
proprietaria di 1 unità di capitale;
• ciascuna di queste imprese assume L lavoratori a cui paga un
salario W stabilito dal mercato;
• ciascuna impresa vende Y unità di prodotto al prezzo P
stabilito dal mercato
La domanda di lavoro
• L’obiettivo dell’impresa è quello di massimizzare il suo
profitto, ossia la differenza tra i suoi ricavi e i suoi costi (per
ipotesi, gli unici costi sono rappresentati dai salari pagati ai
lavoratori):
profitto = ricavi – costi = (P Y) – (W L)
• Per realizzare questo obiettivo, l’impresa aumenta la
produzione assumendo lavoratori fino a quando il ricavo
marginale generato dall’ultimo lavoratore assunto eguaglia il
suo costo di assunzione rappresentato dal salario:
(P PML) – W = 0
La domanda di lavoro
• Il prodotto marginale del lavoro PML è la differenza tra quanto
l’impresa è in grado di produrre con la sua forza lavoro
corrente Limpresa e quanto produrrebbe se assumesse 1
lavoratore addizionale.
• In simboli, se la funzione di produzione dell’impresa
rappresentativa è Yimpresa = F(1, Limpresa), dove 1 rappresenta 1
unità di capitale, il prodotto marginale del lavoro è dato da:
• PML = F(1, Limpresa + 1) – F(1, Limpresa)
La domanda di lavoro
Se la funzione di produzione dell’impresa rappresentativa è
espressa nella forma di una Cobb-Douglas Y = 1(LE)1- (con
K=1, per ipotesi) , il prodotto marginale del lavoro può essere
calcolato derivando la funzione rispetto ad L e ottenendo:
PML =
(1 - )E 1-
Limpresa
L’impresa assumerà lavoratori fino al punto in cui il valore del
prodotto marginale (PxPML) è uguale al salario:
P
(1 - )E 1-
Limpresa
= W
La domanda di lavoro
• L’impresa tipica sceglie
di assumere il numero di
lavoratori che rende il
ricavo marginale – il
prodotto marginale del
lavoro moltiplicato per il
prezzo del prodotto P –
uguale al salario W. In
questo punto, la curva
del ricavo e la curva del
costo sono parallele e il
profitto è massimizzato.
La domanda di lavoro
• Dalla condizione di eguaglianza tra ricavo marginale (PxPML)
e costo marginale (W)
P
(1 - )E 1-
Limpresa
= W
possiamo derivare un’espressione per la domanda di lavoro di
un’impresa tipica (Limpresa):
1
Limpresa
1 E 1
=
W
/
P
La domanda di lavoro
• La domanda di lavoro nell’intero sistema economico (K
imprese) sarà uguale a K volte la domanda di lavoro
dell’impresa tipica:
1
Ld = K
1 E 1
W
/
P
• Come si nota, vi è una relazione inversa tra domanda di lavoro
e salario reale.
L’equilibrio del mercato del lavoro
• L’equilibrio nel mercato del lavoro si realizza quando
domanda e offerta di lavoro sono uguali. Abbiamo determinato
la domanda di lavoro complessiva del sistema economico.
Come si determina l’offerta di lavoro?
• L’offerta di lavoro è rappresentata semplicemente da chi
desidera lavorare, ossia dalla forza lavoro.
• Sotto l’ipotesi di perfetta flessibilità di prezzi e salari, è
possibile che ci sia un divario tra domanda di lavoro delle
imprese e forza lavoro? La risposta è no. Vediamo perché.
L’equilibrio del mercato del lavoro
• Supponiamo che i lavoratori disposti a lavorare al salario e ai
prezzi correnti siano in numero maggiore rispetto alla
domanda di lavoro delle imprese. In questa situazione, la
concorrenza tra lavoratori provocherà un abbassamento del
salario W e quindi, per un dato livello dei prezzi, una riduzione
del salario reale W/P inducendo le imprese ad assumere
lavoratori.
• Se invece la richiesta di lavoratori da parte delle imprese
eccede la forza lavoro, la concorrenza tra imprese per
accaparrarsi lavoratori provocherà un innalzamento del salario
reale W/P e quindi una riduzione della domanda di lavoro.
L’equilibrio del mercato del lavoro
• La flessibilità salariale è alla base del meccanismo di market
clearing che porta in equilibrio il mercato del lavoro.
• Formalmente, il salario reale di equilibrio può essere derivato
dall’eguaglianza tra domanda di lavoro Ld e forza lavoro L :
1
1
1
E
d
L = L = K
W
/
P
• Risolvendo per W/P, si ha:
W
Y
1 K
1 E
1
P
L
L
L’equilibrio del mercato del lavoro
• Il livello di equilibrio
dell’occupazione è
uguale alla forza
lavoro. Al livello di
equilibrio del salario
reale, non vi è
eccesso di
domanda né
eccesso di offerta di
lavoro.
L’equilibrio del mercato del lavoro
• Fino a quando la flessibilità salariale consente il meccanismo
di market clearing, il sistema economico opererà in condizioni
di pieno impiego.
• E’ importante notare che la situazione di piena occupazione
non necessariamente garantisce un benessere sociale elevato. I
redditi reali delle persone non proprietarie dei mezzi di
produzione sono i loro salari reali: W/P = (1-α) x (Y/L). Se α è
molto elevato, i redditi dei salariati potrebbero essere molto
bassi e così pure il benessere sociale.
Occupazione e produzione
• Quando il mercato del lavoro è in equilibrio,
l’impresa rappresentativa produce un output pari a:
Yimpresa = 1E 1-(L/K) 1-
(se K è il numero delle imprese esistenti, L/K è la
quantità di lavoro impiegata da una singola impresa)
Occupazione e produzione
• Quando i mercati funzionano bene (equilibrio
concorrenziale e flessibilità di prezzi e salari), la
produzione totale effettiva sarà uguale a quella
potenziale del sistema economico:
Y = K Yimpresa= K x 1E 1-(L/K) 1- = KE 1-L1- =
= K(LE) 1- = Y*
Occupazione e produzione
• Quando il sistema
economico è in
condizioni di piena
occupazione, il
livello di
occupazione è
uguale alla forza
lavoro e il PIL
reale è uguale alla
produzione
potenziale Y*
SEMPLIFICANDO IL LATO DELL?OFFERTA
• Funzione di produzione aggregata nel
modello neoclassico Y=F(N)
• stabilisce il livello di produzione
associato al pieno impiego della forza
lavoro
• L’economia tramite il meccanismo dei
prezzi e dei salari realizza la piena
occupazione
• Se i prezzi e i salari nominali sono perfettamente flessibili
anche i salari reali sono perfettamente flessibili. Secondo gli
economisti classici questo significa che il mercato del lavoro è
sempre in equilibrio.
• Assumiamo che ci sia un raddoppio dei prezzi dei beni finali e
che non si sposti né la domanda né l’offerta di lavoro. A parità
di salario nominale, il salario reale si dimezza e nel mercato
del lavoro ci sarebbe un eccesso di domanda di lavoro.
• L’aumento della domanda di lavoro porterà a un aumento del
salario nominale e quindi anche di quello reale
• Solo quando il salario nominale sarà raddoppiato (al pari dei
prezzi) il salario reale sarà ritornato al livello precedente e il
mercato sarà di nuovo in equilibrio. Il livello dei prezzi
quindi non ha effetti sui salari reali e sull’occupazione
Offerta aggregata classica
• la funzione di offerta aggregata mostra la quantità di
prodotto che le imprese desiderano offrire ai vari
prezzi.
• Stabilito l’equilibrio nel mercato del lavoro e il livello
massimo di output che è possibile ottenere da quella
quantità di lavoro, la quantità di prodotto offerto è
sempre pari al prodotto di piena occupazione ed è
indipendente dal livello dei prezzi
• nel modello neoclassico, quindi, la curva di offerta
aggregata sarà rappresentata da una retta
perpendicolare all’asse delle ascisse
Offerta aggregata
Offerta aggregata e prodotto reale
AS
P
P1
Una diminuzione
dei prezzi non modifica
il livello dell’output
P2
Y*
Y
Il lato della domanda
(la spesa totale)
• Come sappiamo, in un’economia aperta, la spesa totale è
divisa in quattro componenti: consumi (C) investimenti (I),
spesa pubblica (G) ed esportazioni nette (NX)
• La somma di queste quattro componenti costituisce il reddito
nazionale che, secondo il principio del flusso circolare, è
uguale alla domanda aggregata (E) e al PIL reale (Y) :
C + I + G + NX = E = Y
• Ricordiamo quali sono le determinanti di ogni singola
componente della spesa totale
La spesa in consumi
• Le famiglie prendono decisioni su consumo e risparmio dopo
aver versato una parte del loro reddito alla pubblica
amministrazione sotto forma di imposte nette (imposte meno
trasferimenti). Assumiamo che le imposte nette siano ottenute
moltiplicando l’aliquota media costante t per il reddito
nazionale:
T=tY
• Assumere t come costante è una semplificazione del mondo
reale perché nella maggior parte dei paesi industrializzati il
sistema di imposizione fiscale è progressivo
La spesa in consumi
• Il reddito che resta alle famiglia dopo aver pagato le imposte è
il reddito disponibile YD :
YD= Y – T = (1 – t)Y
• Al fine di accrescere il loro patrimonio e la spesa nel futuro, le
famiglie detengono una parte del loro reddito disponibile sotto
forma di risparmio SH . La quota del reddito delle famiglie
destinata all’acquisto di beni di consumo sarà, allora, pari a:
C = YD – SH = Y- T – SH
• Nei principali paesi avanzati i consumi sono pari ai 2/3 del PIL
La spesa in consumi
• Assumiamo che la spesa in consumi venga suddivisa in una
parte che non dipende dal reddito e che denotiamo con C0
(livello di consumi di base) e in una parte che è funzione
positiva del reddito disponibile Cy x YD (il parametro Cy è la
propensione marginale al consumo). Possiamo allora
esprimere la spesa in consumi come una funzione lineare del
reddito:
C = C0 + Cy YD = C0 + Cy (1 – t)Y
• Questa funzione del consumo è una semplificazione del
mondo reale. Le determinanti del consumo non si esauriscono
nel solo reddito disponibile.
Altre determinanti della spesa in consumi
La funzione del consumo
• La funzione del consumo è espressa in forma lineare. Il
parametro C0 (intercetta) è il livello del consumo quando il
reddito disponibile è zero (può essere interpretato come l’ammontare
del patrimonio a cui le famiglie devono rinunciare al fine di restare in vita
in assenza di reddito)
• La propensione marginale al consumo (PMC), denotata dal
parametro Cy (inclinazione) , indica di quanto variano i
consumi se il reddito disponibile varia di 1 euro.
• Cy > 0: se il reddito aumenta, le famiglie accrescono il
consumo. Cy < 1: quando il reddito aumenta, le famiglie
aumentano anche il risparmio
Funzione del consumo
La funzione del consumo può essere rappresentata
in forma lineare come:
C c0 cyY
c0 0,
0 cy 1
Dove cy=C/ Y è la propensione marginale al
consumo e cC 0 rappresenta il consumo autonomo
La funzione del consumo
• Il valore della PMC dipenderà anche dalle aspettative delle
famiglie circa le variazioni del loro reddito. Se la variazione
del reddito è percepita come permanente, allora è tanto più
probabile che la PMC sia relativamente elevata. Se invece la
variazione del reddito è percepita come transitoria , è
probabile che la PMC assuma un valore più contenuto.
• Sulla base delle ipotesi semplificatrici adottate, i due parametri
C0 e Cy sono allora sufficienti per calcolare il livello della
spesa totale in beni di consumo C in corrispondenza di ogni
possibile livello del reddito disponibile YD
La funzione del consumo
C= 250 + 0,7 Yd
• Algebricamente la funzione del consumo sopra
descritta ci dice che il consumo autonomo
(intercetta con l’asse delle ordinate) è 250,
mentre la PMC = 0,7 (inclinazione della
funzione). Il suo significato è che se il reddito
aumenta di 1 euro, 0,70 euro vengono spesi per
beni di consumo e 0,30 vengono risparmiati.
• Poiché tutto il reddito può essere consumato o
risparmiato dalla funzione del consumo si
deriva quella del risparmio
Esempio numerico
YD
C
S
1000
900
100
2000
1800
200
3000
2700
300
Qual è la PMC e la PMS?
Dall’esempio precedente:
PMC= C/ YD= 1800-900/1000= 0,9
La variazione del consumo per ogni data
variazione di reddito è 0,9 (costante)
PMS= S/ YD= 200-100/1000= 0,1
La variazione del risparmio per ogni data
variazione di reddito = 0,1= costante
s+ c1= 0,9+ 0,1 =1
Inclinazione e spostamenti della FC
• Se cy aumenta la FC diventa più inclinata.
Questo significa che per ogni variazione di
reddito disponibile si genera una maggiore
variazione del consumo
• Se c0 aumenta, perché per esempio aumenta la
fiducia dei consumatori, la funzione si sposta
verso l’alto (cambia l’intercetta)
• Se Yd aumenta o diminuisce il cambiamento
nel consumo si misura lungo la curva
Risparmio= reddito residuale
• S= Y-C
• S= Y- (c0 + cyY)
• che si può anche scrivere riaggiustando i
termini:
• S= - c0 + (1- cy) Y (funzione del risparmio)
• NB: - c0 è l’intercetta della funzione del
risparmio
• (1- cy) è l’inclinazione della F. del risparmio
Funzione del risparmio
risparmio
Inclinazione
= PMS
S= -c0+(1-cy)Yd
S=0
S
Yd
0
-c0
reddito
Caratteristiche della funzione del risparmio
• La funzione del risparmio mostra il risparmio
programmato per ogni livello di reddito.
• L’intercetta è pari al consumo autonomo ma
con segno negativo.Infatti se il reddito
disponibile è pari a zero, allora S= -c0.
• La propensione marginale al risparmio è
invece una misura della variazione del
risparmio per una data variazione del reddito
disponibile
La spesa in investimenti
• La spesa in investimenti è la componente più variabile e
volatile del PIL
• Per dare un’idea dell’ordine di grandezza, nel caso degli USA
essa ammonta attualmente a circa il 17% del PIL
• Le cause delle fluttuazione della spesa in beni di investimento
sono principalmente due: il tasso di interesse e gli animal
spirits degli imprenditori
• Tasso di interesse. Più alto (basso) è il tasso di interesse reale,
più bassa (alta) è la spesa in investimenti perché diventa più
costoso (meno costoso) per le imprese intraprendere progetti di
investimento
• Animal spirits. Più alta (bassa) è la fiducia degli imprenditori,
più elevata (bassa) sarà la spesa in investimenti
Ancora su investimenti e tasso di interesse
• Le imprese investono quando il rendimento dell’investimento,
ossia il flusso dei profitti futuri attualizzati, è maggiore del
costo dell’investimento stesso. Quanto maggiore è il tasso di
interesse, e quindi il costo dell’investimento, tanto minore sarà
il numero di progetti di investimento potenzialmente redditizi.
Al livello aggregato, vi è quindi una relazione inversa tra tasso
di interesse e spesa in investimenti.
• Ma qual è il tasso di interesse rilevante? E’ il tasso di interesse
reale rischioso a lungo termine.
• A lungo termine, perché i progetti di investimento influenzano
costi e profitti dell’impresa in un lungo arco di tempo
• Reale, ossia corretto per l’inflazione, perché l’investimento
intrapreso dall’impresa è rappresentato da un’attività materiale
e non da un titolo finanziario
• Rischioso, perché i progetti di investimento sono “rischiosi” in
quanto sono basati su aspettative che riguardano il futuro
La funzione di investimento
• Assumiamo che anche la funzione di investimento sia espressa
in forma lineare:
I = I 0 – Ir r
dove I0 sono gli investimenti di base (intercetta) e Ir r è la
parte degli investimenti che dipendono inversamente dal tasso
di interesse reale r (Ir è la sensibilità degli investimenti al tasso di
interesse, ossia la pendenza della funzione di investimento)
La funzione di investimento
Altre determinanti degli investimenti
• Come nel caso della funzione del consumo, anche nel caso della funzione
degli investimenti abbiamo adottato una grande semplificazione della
realtà.
• Nel mondo reale le decisioni di investimento dipendono non solo dal tasso
di interesse reale ma anche dalle risorse finanziarie delle imprese e dai
profitti totali. Inoltre, alcune componenti degli investimenti (costruzioni)
sono molto sensibili alle variazioni di r , altre invece sono poco sensibili
(investimenti in scorte delle piccole imprese)
• Il livello di spesa in investimenti può anche essere espressa come funzione
del livello del mercato azionario in quanto gli stessi fattori che determinano
il valore del mercato azionario determinano anche il livello della spesa in
investimenti. Infatti, quando r è basso, gli investitori preferiscono le azioni
alle obbligazioni e questo fa salire il mercato azionario al pari degli
investimenti delle imprese. Analogamente, se gli utili futuri attesi sono
elevati, il valore del mercato azionario salirà e così pure gli investimenti
delle imprese
Acquisti pubblici
• Gli acquisti pubblici di beni e servizi nelle principali economie
industrializzate costituiscono circa il 25% del PIL, includendo
gli acquisti delle pubbliche amministrazioni locali, statali e
federali
• La spesa pubblica è maggiore degli acquisti pubblici in quanto
include i trasferimenti che, nella contabilità nazionale,
vengono considerati come imposte negative
• Nel nostro modello, gli acquisti pubblici sono indicati dalla
variabile G che è assunta come esogenamente determinata. Al
pari della contabilità nazionale, assumiamo i trasferimenti
come imposte negative (come si è visto, abbiamo definito le
imposte come imposte nette).
Acquisti pubblici, trasferimenti e
imposte
Commercio internazionale
• L’ultima componente del PIL da considerare sono le
esportazioni nette (NX), ossia la differenza tra esportazioni
lorde (GX) e importazioni (IM)
• Sommando le esportazioni nette NX a C+I+G, teniamo
conto delle produzioni nazionali vendute agli stranieri e che
non compaiono in C+I+G ; inoltre, correggiamo la spesa dei
residenti per escludere i beni di produzione estera che non
attivano il PIL nazionale
• La funzione di comportamento delle esportazioni nette è
ovviamente il risultato combinato delle due funzioni di
comportamento riferite rispettivamente alle esportazioni lorde
e alle importazioni
Esportazioni lorde
• Il volume delle esportazioni lorde (GX) di un paese dipende
positivamente da due variabili: il reddito estero (Yf) e il tasso
di cambio reale (ε):
GX = (Xf Yf) + (X )
dove:
Xf è la sensibilità delle esportazioni nazionali al reddito estero (GX/
Yf) ;
X è la sensibilità delle esportazioni nazionali al tasso di cambio reale
(GX/ );
(Nota bene il tipo di notazione utilizzata per i parametri: la lettera
maiuscola indica la variabile della quale vogliamo misurare la reattività mentre
il pedice fa riferimento alla variabile rispetto alla quale vogliamo misurare tale
reattività ( variabile esplicativa contenuta nel secondo membro)
Importazioni
• La domanda di importazioni (IM) dipende positivamente dal
PIL reale interno (Y). Dipende (negativamente) anche dal tasso
di cambio reale, nel senso che un deprezzamento
(apprezzamento), rendendo le merci straniere più (meno)
costose, provoca una riduzione (aumento) dei beni importati.
Tuttavia, per semplicità, nel nostro modello assumiamo che le
importazioni IM sono espresse come una quota costante del
Pil reale Y:
IM = IMy x Y
(dove IMy è la propensione marginale ad importare; 0< IMy <1)
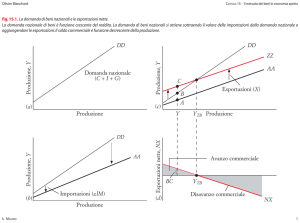
Rappresentazione grafica
Al livello di reddito Y0 il
saldo della BC=0
import
deficit
esportazioni
surplus
Y0
Y
La funzione delle esportazioni nette NX
• Mostra la differenza tra esportazioni e
importazioni in funzione del reddito nazionale.
surplus
Surplus o
deficit
deficit
0
NX=GXIM
Y0
Funzione delle NX
Date le esportazioni, un
aumento del reddito
interno aumenta le
importazioni e riduce le
esportazioni nette (GX-IM)
NX
NX=0
Y
Esportazioni nette
• Definiamo le esportazioni nette (NX) come la differenza tra le
esportazioni lorde (GX) e le importazioni (IM):
NX = GX – IM = (Xf Yf) + (X ) – (IMy Y)
• Quindi le esportazioni nette NX dipendono positivamente dal
reddito estero Yf e dal tasso di cambio reale , e negativamente
dal reddito interno Y
Esportazioni nette e curva J
• Come nel caso delle altre determinanti della domanda aggregata, anche nel
caso delle esportazioni nette abbiamo semplificato notevolmente la
funzione di comportamento. Le NX dipendono anche da altri fattori
(pensiamo, per esempio, al ruolo della politica commerciale).
• Inoltre, l’impatto del tasso di cambio reale sulle esportazioni nette opera
con una serie di ritardi: una variazione di nell’anno corrente avrà uno
scarso effetto sulle NX nell’anno in corso; gli effetti saranno visibili solo
dopo qualche anno. Anzi, nell’anno corrente, un eventuale deprezzamento
del cambio reale può determinare un peggioramento del valore delle
esportazioni nette, anziché un miglioramento. La ragione di questo
risultato è che nel breve periodo il deprezzamento provoca un immediato
aumento dei prezzi dei beni importati senza una sostanziale variazione dei
volumi dei beni importati ed esportati. Questo effetto perverso delle
variazioni del tasso di cambio sulle esportazioni nette può essere
rappresentato con una curva a forma di J: al momento del deprezzamento le
NX peggiorano repentinamente per poi migliorare progressivamente con il
passare del tempo
Gli effetti sul saldo della BC
Saldo della BC
prima peggiora
e poi migliora
Saldo
BC
0
Tempo, t
La curva J è la rappresentazione
grafica dell’aggiustamento dinamico
della BC in seguito a un
deprezzamento reale
L’effetto J è dovuto ai seguenti fattori
• Valuta di fatturazione (i beni esteri sono fatturati in
valuta estera e rende immediatamente più care le
importazioni e non modifica il deprezzamento il valore
delle esportazioni che sono fatturate in valuta nazionale
• durata dei contratti . Alcuni contratti stipulati
anteriormente alla svalutazione devono essere eseguiti in
date future e le quantità prefissate con mesi di anticipo non
possono essere modificate.
• Rigidità della domanda di alcuni beni importati
(macchinari, materie prime) a variazioni del tasso di
cambio reale
Il tasso di cambio
• Abbiamo visto come il tasso di cambio sia un’importante
variabile esplicativa delle esportazioni nette. Chiediamoci ora
che cosa determina il tasso di cambio
• Coloro che operano sul mercato dei cambi scambiano titoli
denominati in differenti valute per trarne un profitto. Due sono
i moventi alla base dell’attività degli operatori: avidità e paura
• Avidità. Se, per esempio, vengono osservati interessi più
elevati su titoli statunitensi piuttosto che su quelli europei, un
operatore potrà ottenere un profitto vendendo titoli europei
(“in posizione corta”) ed acquistando titoli statunitensi (“in
posizione lunga”). Quanto maggiore sarà il differenziale tra
tasso di interesse statunitense e tasso di interesse europeo,
tanto maggiore sarà il guadagno dell’operatore.
Il tasso di cambio
• Paura. Sempre con riferimento all’esempio precedente,
l’attività dell’operatore sarà condizionata anche dalla paura di
un deprezzamento del dollaro, evento che potrebbe cancellare i
profitti derivanti dal differenziale di interesse perché la
variazione del cambio comporterebbe una perdita in conto
capitale. Un deprezzamento del dollaro sarà tanto più
probabile quanto più il tasso di cambio corrente è apprezzato
(più basso) rispetto al suo valore medio o di lungo periodo
• Equilibrio. L’equilibrio sul mercato dei cambi si determina
quando avidità e paura si compensano: quanto maggiore è il
fattore avidità derivante da un elevato differenziale dei tassi di
interesse tanto maggiore dovrà essere la paura di un
deprezzamento e quindi tanto più basso dovrà essere il valore
corrente del tasso di cambio (cambio apprezzato rispetto al
valore medio)
Il tasso di cambio
• Le relazioni precedenti permettono di determinare il tasso di
cambio reale corrente. L’equazione che segue esprime il tasso
di cambio reale corrente in funzione del suo valore medio (di
lungo periodo) 0 e del differenziale tra tasso di interesse
interno r e tasso di interesse estero rf :
= 0 - r (r – rf)
• (Il parametro r è la sensibilità del tasso di cambio reale corrente al
differenziale di interesse)
• L’equazione di determinazione del tasso di cambio reale
corrente può essere illustrata dal seguente grafico
Il tasso di cambio
Aspettativa di deprezzamento della valuta nazionale
r>rf
Aspettativa di apprezzamento della
valuta nazionale
ra= rf
r <rf
ε
ε0 ε
Tasso di cambio ed esportazioni nette
• Se prendiamo l’equazione delle esportazioni nette
NX = GX – IM = (Xf Yf) + (X ) – (IMy Y)
possiamo sostituire in essa l‘espressione per derivata dall‘equazione di
determinazione del tasso di cambio reale corrente vista in precedenza,
ottenendo:
NX = (Xf Yf) +(X 0) – (X r r)+(X r rf) – (IMy Y)
Questa equazione segnala come il tasso di interesse interno e quello estero
influenzino le esportazioni nette in via diretta, senza passare per il tasso di
cambio
CONCLUSIONI
• Abbiamo rivisto il modello a prezzi flessibili
• Esiste equilibrio nel mercato del lavoro
• La funzione del consumo va rivista: se consideriamo variabili
come la ricchezza, gli incrementi di reddito permanenti distinti
da quelli temporanei ( risultato la PMV e PMC nel lungo
periodo sono più alte di quelle di breve periodo
• La funzione degli investimenti tiene conto delle aspettative
(animal spirits)
• Le esportazioni nette sono funzione negativa del reddito
interno
• Esiste equilibrio nel mercato dei beni pur dopo aver introdotto
le complicazioni viste