area tra una funzione e l`asse x

A
AR
RE
EA
AT
TR
RA
AU
UN
NA
AF
FU
UN
NZ
ZIIO
ON
NE
EE
EL
L’’A
ASSSSE
EX
X
Data una funzione y  f x  , per calcolare l’area della parte di piano compresa tra tale funzione
e l’asse delle ascisse in un intervallo a, b si utilizza l’integrale definito.
Si distinguono tre casi a seconda del segno della funzione
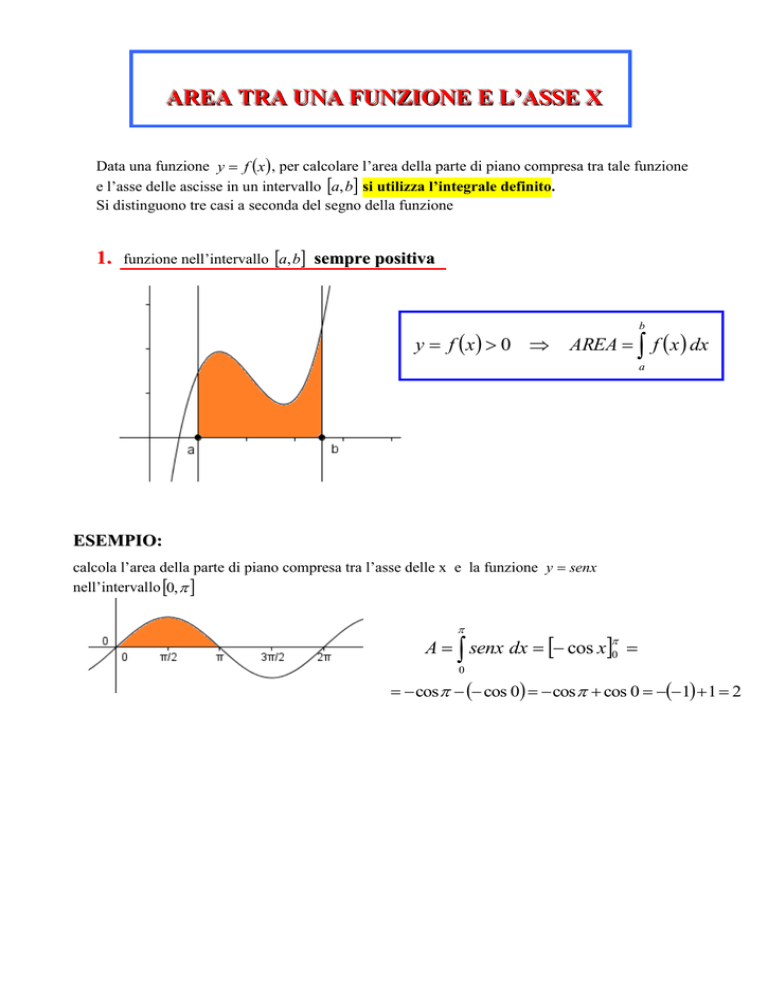
1.
funzione nell’intervallo a, b sempre positiva
y  f x   0 
b
AREA   f x  dx
a
ESEMPIO:
calcola l’area della parte di piano compresa tra l’asse delle x e la funzione y  senx
nell’intervallo 0,  

A   senx dx   cos x0 
0

  cos    cos 0   cos   cos 0  1  1  2
2.
funzione nell’intervallo a, b sempre negativa
b
y  f x   0 
AREA   f x  dx
a
N.B.
Dato che l’area non può dare come
risultato un valore negativo è necessario
cambiare segno al valore dell’integrale
ESEMPIO:
calcola l’area della parte di piano compresa tra l’asse delle x e la funzione y  senx
nell’intervallo  ,2 
2
A    senx dx   cos x  cos x

2
 cos 2  cos  ]  1   1  2
2
La funzione nell’intervallo a, b ha un punto di intersezione con l’asse x
3.
e il suo grafico è in parte positivo, in parte negativo
L’intervallo a, b viene diviso dal valore di c in cui la
funzione attraversa l’asse x in due parti a, c e c, b
AREATOT  A1  A2
A1
c

A1  f x  dx
in a, c risulta f x   0 quindi
a
A2
b

A 2   f x  dx
in c, b risulta f x   0 quindi
c
Quindi
c
b
a
c
ATOT   f x  dx   f ( x)dx
ESEMPIO:
calcola l’area della parte di piano compresa tra l’asse delle x e la funzione y  cos x
nell’intervallo 0,2 

2
3

2
0

senx 02  senx 
 senx 3
3

2
2
2
ATOT   cos x dx   cos x dx   cos x dx =

2

2
3
 
3 

 
  sen  sen 0    sen   sen    sen 2  sen   
2
2
2 
2 

 

3

3
 sen  sen 0  sen   sen  sen 2  sen  
2
2
2
2

3
2sen  2 sen   sen 0  sen 2  2  1  2   1  1  1  4
2
2
3

2
2

=
ESERCIZIO:
y
determinare l’area tra la funzione
2x  3
e l’asse delle ascisse nell’intervallo 1,3
x
 Devo conoscere il segno della funzione e scoprire se ha punti di intersezione con l’asse x
Per fare ciò è necessario fare il grafico ( se è possibile) oppure studiare il segno della funzione e
cercare i suoi punti di intersezione con l’asse x
In questo caso posso utilizzare sia un metodo che l’altro:
GRAFICO
y
2x  3 2x 3
3

  2
x
x x
x
è una iperbole traslata
3
x
si costruisce poi il grafico di y  y1  2 traslando il grafico precedente verso l’alto
Cioè partendo dal grafico di y1  
Dal grafico si scopre che la funzione
nell’intervallo 1,3
 è continua
 ha un punto di intersezione B con l’asse x
(devo determinare le sue coordinate)
 riguardo al segno
in 1, b f ( x)  0
in b,3 f ( x)  0
Quindi
b
3
1
b
ATOT   f x  dx   f ( x)dx
è necessario ancora conoscere le coordinate del
punto B ( vedi dopo )
CALCOLI ALGEBRICI
y
2x  3
x
 Intersezioni con asse x ( y=0 )
2x  3
3
3 
0
2x  3  0
x
quindi la funz. ha in 1,3un punto di intersezione B ,0 
x
2
2 
 Segno
2x  3
0
x
N 0
2x  3  0
D0
x0
x
3
2
3
2
0
N
D
Quindi
 3
in 1,  f ( x)  0
 2
+
_
+
3 
e in  ,3 f ( x)  0
2 
 Posso disegnare una grafico approssimativo e visualizzare la parte di piano di cui è richiesta
l’area
3
2
ATOT
2x  3
2x  3
 
dx  
dx 
x
x
3
1
3
2
3
2
3
3
3
   2  dx   2  dx  ........
x
x
3
1
2
A
AR
RE
EA
AT
TR
RA
AD
DU
UE
EF
FU
UN
NZ
ZIIO
ON
NII
1.
aarreeaa ccoom
mpprreessaa ttrraa dduuee ffuunnzziioonnii iinn uunn iinntteerrvvaalllloo
Data due funzioni y  f x  e y  g x  vogliamo calcolare l’area della parte di piano compresa
tra tali funzioni in un intervallo .a, b

f(x)
Supponendo che sia f x  g (x)
come nella figura a fianco
ATOT  AABDE  AABC
cioè
b
b
a
a
ATOT   f x  dx   g ( x)dx
g(x)
 Se invece f x  g (x) allora è il contrario
2.
aarreeaa ccoom
mpprreessaa ttrraa dduuee ffuunnzziioonnii
Se le due funzioni si intersecano tra loro, l’intervallo da prendere in considerazione è quello
determinato dai punti di intersezione A e B
ESEMPIO: determinare l’area tra
f x   x 2  2 x  3 e g x    x 2  x  5
A
f(x)
 devo fare il grafico per capire quale delle due funzioni
ha un grafico più in alto rispetto all’altra
(vedi figura)
g(x)
B
 Trovo i punti di intersezione tra le due funzioni
 In questo caso è f x  g (x) quindi


b
b
a
a
ATOT   g x  dx   f ( x)dx
b
Per la proprietà degli integrali definiti si può scrivere anche ATOT  [ g x   f ( x)]dx

a
 SVOLGO L’ESERCIZIO
 Trovo i punti A e B di intersezione tra le due funzioni
 y  x 2  2x  3

2
 y  x  x  5
 x 2  2x  3  x 2  x  5
 2 x 2  3x  2  0
x
3  9  16
4
xB  2
1
xA  
2
 Calcolo l’area
2
ATOT 
2
2
)  f ( x)]dx
 g x  dx   f ( x)dx   [ g ( xvedi
proprietà degli integrali

1
2

2
1
2


1
2

ATOT   [(  x  x  5)  x  2 x  3 ]dx 
2

2
1
2
2
 (2 x

2
 3x  2)dx 
1
2
2


x3
x2
4
 8
  2  1 3 1 
  2  3  2 x    2  3  4         1  .....
3
2
2
  3  8 2 4 

 1  3
2
F(b)
=………..=
-
F(a)
3.
aarreeaa ccoom
mpprreessaa ttrraa ppiiùù ffuunnzziioonnii
Facendo riferimento alla TERZA PROPRIETA’ degli integrali definiti quanto abbiamo già
detto riguardo all’esempio precedente, si può calcolare anche in questo modo
b
b
b
a
a
a
a
b
ATOT   g x  dx   f ( x)dx   g ( x)dx   f ( x)dx
Per tale motivo per calcolare l’area della parte di piano compresa tra tante funzioni
 Si determinano i punti di intersezione
 Partendo uno di tali punti
SI PERCORRE IL PERIMETRO
DELLA FIGURA IN SENSO
ANTIORARIO
 Si calcola l’integrale per ogni tratto
quindi
b
ATOT 
c
a
 hx  dx   g ( x)dx  
a
mi sposto da A a B
percorrendo un
tratto della funz. h
b
mi sposto da B a C
percorrendo un
tratto della funz. g
f ( x)dx
c
mi sposto da C a A
percorrendo un
tratto della funz. f