17.07.02

Prova scritta dell’esame di TEORIA DEI SEGNALI
17/07/02
Studente (Cognome Nome)……………………………………………num. matric………………
Esercizio1.
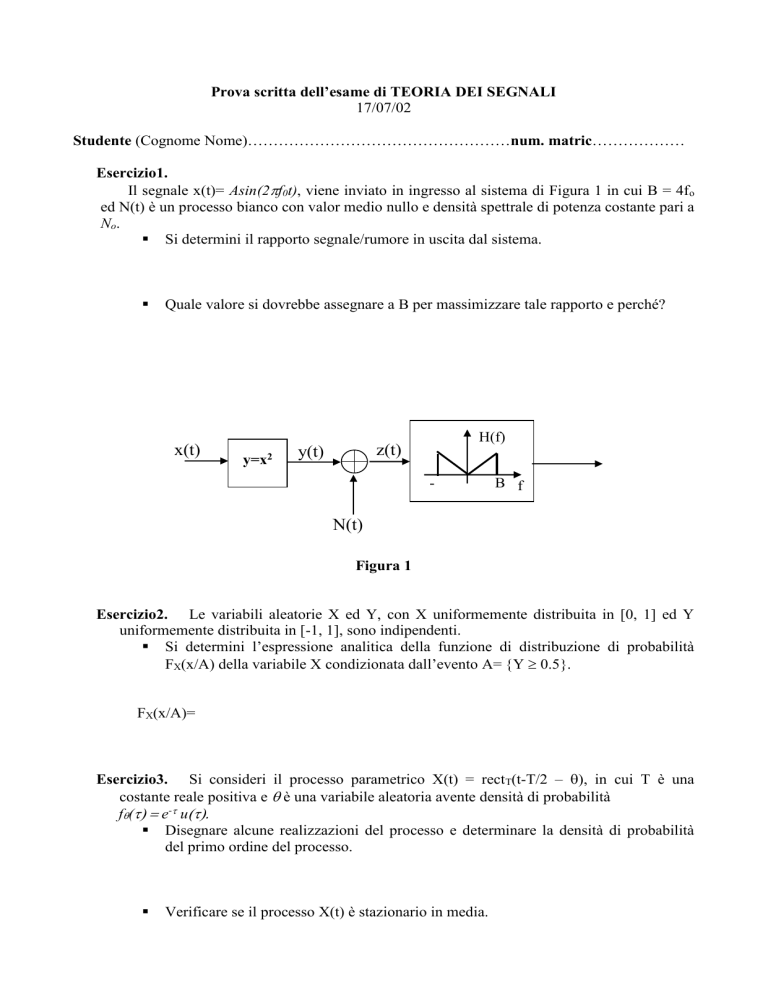
Il segnale x(t)= Asin(2f0t), viene inviato in ingresso al sistema di Figura 1 in cui B = 4f o
ed N(t) è un processo bianco con valor medio nullo e densità spettrale di potenza costante pari a
No .
 Si determini il rapporto segnale/rumore in uscita dal sistema.

Quale valore si dovrebbe assegnare a B per massimizzare tale rapporto e perché?
x(t)
y=x2
H(f)
z(t)
y(t)
B
B f
N(t)
Figura 1
Esercizio2. Le variabili aleatorie X ed Y, con X uniformemente distribuita in [0, 1] ed Y
uniformemente distribuita in [-1, 1], sono indipendenti.
 Si determini l’espressione analitica della funzione di distribuzione di probabilità
FX(x/A) della variabile X condizionata dall’evento A= Y  0.5.
FX(x/A)=
Esercizio3. Si consideri il processo parametrico X(t) = rectT(t-T/2 – ), in cui T è una
costante reale positiva e  è una variabile aleatoria avente densità di probabilità
f(e-u
 Disegnare alcune realizzazioni del processo e determinare la densità di probabilità
del primo ordine del processo.

Verificare se il processo X(t) è stazionario in media.
1° Quesito
Si definisce rapporto Segnale/Rumore in uscita da un sistema il rapporto tra la potenza del segnale
utile e la potenza del rumore.
Nel caso in esame il segnale utile è il segnale xt  che dopo il quadratore si trasforma in yt  quindi
si somma al rumore N t  .
Poiché il rumore N t  si assume incorrelato con il segnale utile, il segnale somma zt   yt   N t 
non contiene componenti di densità spettrale di potenza mutua, cioè
S zz  f   S NN  f   S yy  f 
In uscita dal filtro è quindi possibile distinguere la potenza dovuta al segnale utile e quella dovuta al
rumore.
Come prima cosa consideriamo le trasformazioni che subisce il segnale utile.
Si determina il segnale yt 
yt   x 2 t   A 2 sin 2 2f 0 t  
A2 A2

cos4f 0 t 
2
2
2
Lo spettro di yt  è costituito da una riga nell’origine (componente continua) di ampiezza A
e da una coppia di righe alle frequenze  2 f 0 , ciascuna di ampiezza A
Y f  
2
4
2
e fase  .
A2
A2
  f  2 f 0     f  2 f 0 
  f 
2
4
Il filtro H  f  ha un nullo nell’origine e quindi elimina la componente continua. Inoltre, il filtro ha
banda B  4 f 0 e quindi lascia passare le righe in  2 f 0 . In corrispondenza di tali frequenze la
risposta del filtro vale H  2 f 0   1 . Lo spettro del segnale di uscita utile è quindi
2
Yu  f   
A2
  f  2 f 0     f  2 f 0 
8
Antitrasformando, si trova l’andamento temporale del segnale yu t  , che è
A2
cos4f 0 t  è periodico a potenza finita, quindi la sua potenza è data per il
4
teorema di Parseval da :
il segnale yu t   
PYu   YK
2
K
A2
 2
8
2
A4
32

potenza del segnale utile in uscita dal sistema
Ora consideriamo il rumore N t  e la sua trasformazione.
In uscita dal filtro H  f  otteniamo
S Nu  f   H  f  S N  f 
2
Hf  
f
4 f0
rect 8 f 0  f 

PN u 
 S Nu  f df 

PN u 
8
N0 f0
3
4 f0

4 f0
Hf  
;
f
2
16 f 0
f
2
2
 N 0 df 
2N 0
16 f 0
2
2
16 f 0
4 f0

0
2
rect 8 f 0  f 
f 2 df 
N0
8 f0
2

4 f 0 3
3
potenza del rumore in uscita dal sistema
A4
4
S
32  3 A

N 8 N 0 f 0 256 N 0 f 0
3
S
il filtro deve avere un valore minimo di banda pari a quella
N
del segnale utile in modo da far passare il segnale utile e filtrare il piu’ possibile il rumore in
ingresso.
1b.
Per massimizzare il rapporto
B  2 f0
2° Quesito
La probabilità PX  x / Y  0.5  PX  x dato la statistica indipendenza di X e Y.
Vediamo come si arriva al risultato con la funzione congiunta
FX / A x / A  PX  x / A  PX  x / Y  0.5 
P X  x , Y  0.5 P X  x   Y  0.5

PY  0.5
PY  0.5
Essendo X e Y statisticamente indipendenti f XY x, y   f X x  f Y  y 
Il dominio di definizione di X e Y è illustrato in Fig. 2. L’evento Y  0.5 è rappresentato dal
dominio tratteggiato in Fig. 3, avente area 0.5
f XY x, y   0.5
Y
Y  0.5
Y
1
1
0.5
1
X
1
-1
-1
Fig. 2
Fig. 3
Essendo il dominio di (X,Y) uniforme 
P E  
X
misE 
misD 
ne segue che
1
1
PY  0.5  2 
2
4
Assumendo 0<x<1, l’evento intersezione
colore scuro in Fig. 4, avente area 0.5 x
X  x  Y  0.5 è rappresentato dal dominio di
Y
1
0.5
x
-1
1
X
Fig. 4
Ne segue che
0
0
,x  0


0.5  x

P X  x   Y  0.5  
,0  x  1  x
2
4


,x 1
 1 4
 1 4
,x  0
,0  x  1
,x 1
Dividendo per la probabilità dell’evento Y  0.5 si trova infine
0

FX / A x / A  x
1

,x  0
,0  x  1
,x 1
3° Quesito
Rappresentiamo alcune realizzazioni del processo X t 
X(t)
X(t)
xt ,  0
T
t
xt ,  t1 
t1
t1  T
Il processo X(t) può assumere solo i valori 0 e 1, quindi la sua densità di probabilità del I ordine è
del tipo
f X x, t   p0 t  x   p1 t  x  1
con p1 t   1 p0 t 
Considerando che il ritardo aleatorio (la variabile  ) non può essere piu’ piccolo di 0, si ha che
p0 t   1 ,
Per t<0
p1 t   0
X(t)

Per t>0
t
 T
t
p1 t   P  t    T   P  t , t    T   Pt  T    t  F t   F t  T 
dove F x  è la funzione distribuzione di probabilità della variabile  , che vale
F x   1  exp   u 
Si ottiene quindi
p1 t   1  exp  t  ut   1  exp  t  T  ut  T 
Ricordando che t>0 si ha
p1 t   1  exp  t   1  exp  t  T  ut  T 
Distinguiamo infine i due casi :
0<t<T
t
p1 t   1  exp  t 
t>T
p1 t   1  exp  t   1  exp  t  T   exp  t  T   exp  t  
exp  t   exp T   exp  t   exp T   1  exp  t 
EX t   0  P X t   0  1 P X t   1  p1 t 
il valore medio del processo dipende da t ne segue che X t  non è stazionario neppure in media.