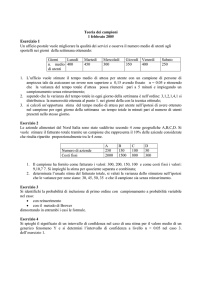
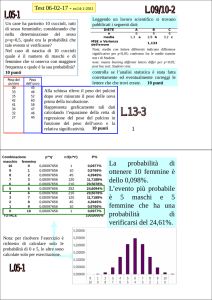
1
Facoltà di Chimica Industriale
LABORATORIO DI FISICA GENERALE
(CORSO B)
a.a. 1999/2000
dr. Maurizio SPURIO
[email protected]
Parte 1: Misure, errori di misura e statistica.
2
INDICE
Errori di misura
Come indicare gli errori di misura
Analisi degli errori casuali
Cenni sul calcolo delle Probabilità
Distribuzioni limite o continue
La distribuzione normale o di Gauss
Media e varianza come migliori stimatori di X e
Propagazione degli errori
Errori “relativi” o percentuali
Esempi sulla propagazione degli errori
Deviazione standard della media delle medie
Medie pesate
Confidenza di una misura
Dati che si distribuiscono lungo una retta
Metodo della regressione lineare
Stima degli errori per la retta di regressione
Linearizzazione di una funzione esponenziale
La distribuzione binomiale
Distribuzione di Poisson
Il test del 2, ossia: come prendere una decisione
Un esempio applicato alla distribuzione di Poisson
Nota: le pagine seguenti sono fotocopie dei lucidi presentati a
lezione. Per questo motivo, non sono autoconsistenti, ma
necessitano delle spiegazioni, dimostrazioni e dei passaggi
presentati alla lavagna durante la lezione. Sono però utili per
aiutare lo studente a prendere appunti, per avere sottomano le
formule da usare nelle prove di laboratorio e per selezionare nei
libri consigliati le parti svolte.
Maurizio Spurio
3
Errori di misura
L’errore in una misura scientifica rappresenta l’inevitabile
incertezza che è presente in ogni misura.
Le incertezze sulle misure sono inevitabili e non eliminabili. Si
può pero’ cercare di ridurle ad un livello “accettabile”.
Il più comune errore, corrisponde alla lettura di scale (metri,
termometri, ohmetri…) sia analogiche sia digitali.
Qualsiasi grandezza fisica è soggetta ad un’indeterminazione.
Ad esempio, il rapporto tra la circonferenza C ed il diametro D
di un cerchio, misurato con differenti strumenti, può essere:
C/D =
3.1 0.2
= 3.16 0.03
= 3.1417 0.0002
= 3.1415927…..
(misura rozza)
(misura più accurata)
(“ con molta cura)
(rapporto matematico)
Il problema di come si stima un dato sperimentale e la
corrispondente incertezza (l’errore a destra del segno ) è
uno dei problemi del corso.
Uno dei metodi per valutare l’errore è quello di effettuare
una sequenza di misure della stessa quantità (errore
statistico)
L’errore sistematico è di natura diversa, e la sua stima è a
volte più complessa.
4
Come indicare gli errori di misura
Una “misura” di una grandezza è la miglior stima della
grandezza stessa, nell’intervallo in cui riteniamo essa si
trovi; ad es. C = (2.375 0.005) m
Nel valore sopra indicato, l’indeterminazione è di 0.5 cm,
dovuta ad es. alla scala di lettura.
In generale, scriveremo:
valore misurato di x = (xb x) unita’
x è l’incertezza stimata su xb.
Durante il corso, impareremo come si stimano x e xb .
CIFRE SIGNIFICATIVE: il valore dell’errore deve essere
arrotondato con una (al più, due) cifre significative.
I RISULTATI della misura devono essere dati con lo stesso
ordine di grandezza (cifra decimale) dell’errore. Ad es:
C/D = 3.256973 0.2
= 3.16 0.03471
= 3.1417 0.0002
NO
NO
SI
Con le potenze di dieci, conviene scrivere (ad esempio, per la
carica elettrica):
qe = (1.62 0.02) 10-19 C
5
Analisi degli errori casuali
Aumentare l’affidabilità della misura = ripetere la misura
Errori casuali possono essere ridotti
Errori sistematici NON possono essere ridotti
La singola misura (es. periodo T del pendolo) può essere
soggetta a molte fluttuazioni (reazione start/stop orologio, attrito
del pendolo con aria, attrito nel meccanismo di oscillazione, modi di
oscillazione nel piano normale) ….
Ciascuna causa può aumentare/diminuire T di una singola
misura. Un errore sistematico influisce sempre nello stesso
verso (es. ritardo dell’orologio)
I metodi statistici forniscono il procedimento per stimare e
ridurre le indeterminazione casuali. Le “sistematiche” sono più
difficili da valutare e da rivelare.
Media di una misura
Supponiamo di aver effettuato N= 10 misure Ti (secondi).
8.16 , 8.14, 8.12 , 8.16, 8.18, 8.17, 8.14, 8.16, 8.15, 8.20
Quale è il valore vero? Una stima è :
Tbest = (media dei valori) = 1/N i Ti = 8.158 s
Per definizione, Tbest è calcolato in modo che i (Ti - Tbest) = 0
(somma delle deviazioni nulla).
6
Una grandezza che esprime la qualità della misura è lo
sparpagliamento attorno al valor medio. Un modo di stimare lo
sparpagliamento, è quello di istogrammare i valori di T.
Il modo matematico per esprimere lo sparpagliamento, è quello
di elevare al quadrato le deviazioni, e sommarle.
Nota: Gli istogrammi degli esempi riportati sono stati generati
con il programma (freeware, ossia distribuito gratuitamente)
PAW del CERN, istallato sul PC presente in laboratorio. Le
istruzioni necessarie per generare tutti gli istogrammi, funzioni,
"fit" etc. sono riportati in appendice e sono a libera disposizione
degli studenti.
Entries = numero di eventi
Mean = Valor medio <x>
RMS = Varianza (vedi sotto)
Negli esempi successivi, (Esempio 1) sono presentati tre diversi
istogrammi (H); la grandezza riportata è il periodo Ti . Il primo
H è "male organizzato". Il secondo ed il terzo hanno un numero
diverso di divisioni lungo l'asse delle x (rispettivamente 15 e 30
divisioni)
Nell'Esempio 2 sono riportati gli H di 20, 100 e 1000 misure di
Ti (30 divisioni lungo l'asse x) . Si possono notare le seguenti
caratteristiche:
Il valor medio non cambia drasticamente
La varianza non cambia drasticamente
La forma dell'istogramma diventa più regolare
all'aumentare del numero degli eventi.
7
Esempio 1
Entries = N. Eventi
Mean = Media RMS= Varianza
ID = 12345 Istogramma male organizzato
ID = 1
15 divisioni larghe 0.30s/15 bin = 0.02 s/bin
ID = 2
30 divisioni larghe 0.30s/30 bin = 0.01 s/bin
8
Esempio 2
Gli stessi dati di prima, con 0.01 s/bin
ID= 3 20 eventi
ID= 4 100 eventi
ID= 5 1000 eventi
La media e la varianza non variano apprezzabilmente!
9
Cenni sul calcolo delle Probabilità
La probabilità di un evento è il rapporto tra il numero dei casi
favorevoli su quello dei casi possibili.
A volte il numero dei casi possibili non è noto (ad es.,
probabilità che un calciatore sia espulso durante una partita;
prob. di rottura di un circuito elettronico…)
In questi casi, si utilizza la frequenza = n/N = numero di
eventi favorevoli n sul numero delle prove fatte N.
Teorema: per
N , la frequenza tende alla probabilità
Enunciati di Kolmogorov:
1. Ad ogni evento A può essere associato uno ed un solo
numero p(A)
2. La probabilità che non accada A è p(A). La probabilità che
accada o non è la certezza, ossia:
p(A)+p(A)=1, da cui 0 p(A) 1.
3. Se due eventi A e B sono mutuamente esclusivi, allora:
p(A+B) = p(A) + p(B) .
4. Se A si verifica se e solo se si verificano B1 e B2, che sono
indipendenti tra loro, allora:
p(A) = p(B1) p(B2)
10
Distribuzioni limite o continue
Una serie di misure può essere ordinata in un istogramma, come
frequenza fk di dati in un dato intervallo.
fk = nk /N = numero eventi nell’intervallo k diviso il numero
totale N di eventi
La proprietà (normalizzazione) delle frequenze: fk = 1
In termini di questo ordinamento, il valor medio e la varianza di
x sono:
x n /N = x f
Sx2 = (x - <x>)2f
<x>
k
k
k
k
k
k
Nella maggior parte dei casi, all’aumentare di N, l’istogramma
tende ad assumere qualche forma semplice e definita.
La distribuzione limite è una funzione continua f(x). Come fk
rappresenta la probabilità che gli eventi siano nell’intervallo k
f(x)dx rappresenta la probabilità di trovare la misura
nell’intervallo dx. Inoltre,
+
-
f(x)dx = 1
Il valor medio e la varianza di una distribuzione continua
possono essere calcolate come:
<x> =
2
Sx =
+
-
-
+
x f(x) dx
(x - <x> )2 f(x) dx
11
La distribuzione normale o di Gauss
Le misure di una grandezza soggetta a molte piccole sorgenti di
errore casuali, e trascurabili errori sistematici, tendono a
distribuirsi su una curva a campana chiamata distribuzione
normale o di Gauss, centrata sul valore vero X.
La curva di Gauss con due parametri: X , è la funzione:
2
2
g(x) = (1/2) e –(x-X) /2
La costante di normalizzazione e’ tale che
+
-
g(x)dx = 1
Utilizzando te tavole degli integrali, si può mostrare che:
+
<x> =
Sx =
-
+
-
x g(x) dx = X
(x - <x> )2 g(x) dx = 2
Ossia: se una variabile e’ distribuita normalmente, il valor medio
corrisponde al parametro X e la varianza al parametro della
curva di Gauss.
Questo ci permette di stabilire il significato della varianza di
una grandezza distribuita normalmente; infatti, in generale
l’integrale:
f(x) dx
b
a
= probabilità di trovare la misura tra a e b
allora:
X+
X-
g(x) dx =(1/2)
X-
X+
2
2
–(x-X)
/2
e
dx =
2
–z
/2 dz = 0.68
= (1/2) e
1
-1
12
ossia: la probabilità di trovare la misura in un intervallo pari ad
una deviazione standard dal “valore vero” e’ del 68%.
La probabilità di trovare la misura entro “ t sigma” da X e’
riportata nel grafico seguente (i valori di P vs. t si possono
leggere nella tabella in basso)
13
Media e varianza come migliori stimatori di X e
Un numero molto grande di misure di una grandezza x tende a
distribuirsi secondo la funzione di Gauss.
Un numero finito di N misure x1, x2… xN può stimare il “valore
vero” X e la varianza della distribuzione.
P(x1)
2
2
–
(x
-X)
/2
1/ e
1
P(x2)
….
2
2
–
(x
-X)
/2
1/ e
2
P(xN)
2
2
–
(x
-X)
/2
1/ e
N
Se le misure sono indipendenti, la probabilità Ptot di avere
quell’insieme delle N letture è il prodotto delle N probabilità:
Ptot = P(x1) P(x2) P(xN) = (1/
N
)
2
2
–
(x
-X)
/2
e i i
X e non sono noti, e debbono essere stimati. La miglior stima è
quella che massimizza la probabilità . Procedimento o metodo
della massima verosimiglianza.
X’ Stima di X
’ = stima di
i (xi – X’) = 0
P/X = 0
X’
= i (xi /N)
P/ = 0
’
= 1/N i (xi – X’)2
14
Ricapitolando:
1. Se le misure di una grandezza sono soggette solo a (molti e
piccoli) errori casuali, la loro distribuzione limite e’ la funzione
di Gauss
2. La migliore stima del valore vero X della popolazione e’ il
valor medio, perché massimizza la probabilità che proprio
quelle N misure siano state ottenute.
3. La miglior stima della larghezza della Gaussiana (sigma) è la
varianza Sx.
4. La larghezza della distribuzione corrisponde alla confidenza
che il 68% delle misure di x cadano nell’intervallo
(valore x misurato) = <x> x
15
Errori “relativi” o percentuali
Spesso è utile ricorrere all’errore relativo di una grandezza.
L’errore (spesso chiamato assoluto) ha le stesse dimensioni
fisiche della grandezza:
(valore di x) = xb x unita’
L’errore relativo è indicato come:
(valore di x) = xb (1 x/xb) unita’
L’errore relativo x/xb è adimensionale; è molto utile nei
calcoli di propagazione degli errori (vedi esempi successivi),
quando una grandezza dipende da molte altre variabili.
Talvolta, moltiplicato per 100 viene chiamato “errore
percentuale”. In tal caso, si aggiunge il simbolo “ %”.
L’errore percentuale fornisce immediatamente la qualità della
misura (ossia, il grado di precisione).
16
Propagazione degli errori
Se la grandezza x e’ distribuita normalmente, con media <x>
varianza x , allora la grandezza (A= costante):
q=A+x
e’ gaussiana, con media <q> = A+ <x> e varianza x
Se la grandezza x e’ distribuita normalmente, con media x e
varianza x , allora la grandezza (B= costante):
q = Bx
e’ gaussiana, con media <q> = B <x> e varianza Bx
Se le grandezze x e y sono distribuite normalmente, con
(rispettivamente) media <x> e varianza x , media <y> e
varianza y , allora :
q= x+y
e’ gaussiana, con media:
varianza:
<q> = <x> + <y>
q =
x2
2
+ y
In generale, se x e y sono variabili gaussiane, allora anche
q = f(x,y ) è gaussiana con:
media:
varianza: q =
<q> = f(<x>,<y>)
(q/x)<x>,<y> x2 + (q/y)<x>,<y>
2
y
17
Esempi sulla propagazione degli errori
1. Lo spessore di una risma di 100 fogli (supposti identici) è
S=3.3 0.1 cm. Determinare lo spessore di un foglio
2. Le quantità di moto (rispettivamente) finali ed iniziali di un
oggetto sono pf = 33.7 0.3 kgm/s e pi = 12.2 0.4 kgm/s .
Calcolare la variazione della quantità di moto.
3. Determinare l’area di un rettangolo di dimensioni
a = 33.12 0.05 mm e b= 12.71 0.07 mm .
4. Il tempo di caduta t di un sasso (inizialmente in quiete) da una
altezza h=14.1 0.1 m è t= 1.6 0.1 s. Determinare g.
Nota: l’incertezza relativa di una variabile q= Axn è
q/q = n x/x
5. Determinare la temperatura T di n=2.2 moli di gas perfetto alla
pressione di 1.0 atm. ed al volume di V=1.2 litri. R è noto con
una precisione dello 0.1%, n e P al 5% e V al 2%.
6. Se = 20o 3o , determinare cos.
7. Determinare l’attività (dicembre 1999) di una sorgente
radioattiva con vita media =(30.0 0.5) y , preparata nel marzo
1967 con attività nominale
Ao = (100 12) Curie
18
Deviazione standard della media delle medie
N misure della grandezza x hanno media <x> e varianza x.
Se ripetiamo N volte la stessa serie di N misure, la grandezza
<x> avrà varianza pari a:
<x> = x/ N
.
La deviazione standard x rappresenta l’incertezza su una
singola misura
Se aggiungiamo altre misure, utilizzando la stessa tecnica, ci
aspettiamo che x non cambi apprezzabilmente.
La media di molte medie non fluttua “troppo” attorno alla
media <x> di una serie di misure. La dispersione delle medie,
<x> = x/ N , decresce lentamente con N.
Occorre ricordare che gli errori sistematici Non diminuiscono
all’aumentare del numero di misure.
(Nell’esempio delle pagine successive, i 1000 valori del periodo T
misurati sono stati suddivisi in 20 sotto campioni, ciascuno di 50
misure. Per ciascun campione è stata calcolata la media e la
varianza. Infine sono state istogrammate le 20 medie calcolate.)
19
ESEMPIO 4 - 20 campioni, ciascuno di 50 misure
di T (solo 10 grafici)
20
Media delle medie al lavoro
Consideriamo le 20 medie ottenute dai precedenti
sottocampioni, ciascuno con 50 misure di T.
La distribuzione della media delle medie ha un certo valor
medio (media delle medie) ed una certa larghezza.
La media delle medie è:
<x> = 8.164 s
La varianza si può ottenere dalla varianza x delle singole
distribuzioni (una delle 20) , diviso (numero di eventi)
<x> = x / N
= x/ 7 = 0.003 s
<x> NON dipende dal numero di campioni (nel nostro
caso, 20). E' sufficiente un solo campione per stimare <x>
<x> corrisponde all'errore statistico delle nostre
misure, ossia è l'errore da associare alla misura di x
21
Medie Pesate
Spesso occorre combinare misure separate, con diverso grado di
precisione. Ad es. in due laboratori diversi sono state effettuate
due misure per la velocità della luce.
Lab. A
cA = xA A
Lab. B
cB = xB B
Com’è possibile combinare le due misure, tenendo conto della
diversa qualità delle misure stesse?
Il metodo della massima verosimiglianza dà la risposta. Infatti,
se al solito P(A) e P(B) sono le probabilità delle due misure, la
probabilità di avere entrambe le misure è:
2
2
2
2
P(A+B) (1/ AB ) exp[-(xA-X) /2 A - (xB -X) /2 B]
2
= (1/ AB ) exp[- /2]
dove
2 = [(xA-X)2/22A + (xB -X)2/22B]
Per il principio della massima verosimiglianza, il miglior valore
per X è quello che massimizza la probabilità, ossia minimizza il
chi quadro 2 (d2/dX) = 0
Questo stimatore, è la media pesata, definita come:
w x
w
N
xw
i 1
N
i 1
i
i
i
wi
1
i2
22
Confidenza di una misura
Siamo giunti a stimare una grandezza x, con un certo valor
medio e deviazione standard della media delle medie
valore di x = <x> <x>
Se confrontiamo il nostro valore di x con un valore atteso, noto
anch’esso con una certa indeterminazione, possiamo stabilire se
le nostre misure sono o meno in accordo con l’aspettazione
entro un certo intervallo di confidenza.
Nel caso di accordo, la differenza tra la misura ed il valore
previsto sarà compatibile con zero.
Esempio (attualità!) : SuperKamiokande misura un rapporto tra il
numero di eventi indotti da neutrini del e neutrini dell’e pari a
R=(1.20 0.12) . La fisica dei Raggi Cosmici prevede un valore
Ratteso = (2.0 0.1). Sono compatibili i due risultati ?
In generale, si stima il rapporto t tra la differenza delle quantità
e l’errore sulla differenza. In gergo t viene spesso chiamato
numero di sigma della differenza. La probabilità che le due
misure siano compatibili è:
se t = 1 Pcompat = 1- 0.68 = 32%
se t = 2 Pcompat = 1- 0.95 = 5%
se t = 3 Pcompat = 1- 0.998 = 0.2%
Misure con t > 2 vengono generalmente considerate
incompatibili. Attenzione: può accadere che a volte misure
incompatibili NON lo siano, per sottostima di errori o per non
identificazione di errori sistematici.
23
Dati che si distribuiscono lungo una retta
Talvolta, un esperimento consiste nella verifica di una relazione
lineare (ad es. v(t) = v0 + gt ) . In generale, del tipo:
.
y=A+Bx
dove A e B sono due costanti incognite, e y ed x due variabili
misurabili.
Noi effettuiamo delle misure dei valori yi in corrispondenza di
altrettanti punti xi . Ci aspettiamo che, entro le incertezze i punti
(xi , yi ) si dispongano lungo una retta
Nel seguito, vedremo di:
1. determinare i parametri A e B dell'equazione
2. verificare se la relazione lineare sussiste (cioè, se i dati sono in
accordo con quanto aspettato).
24
Metodo della regressione lineare
Assumiamo per semplicità che gli errori su x siano trascurabili,
e che quelli su y siano gaussiani. Ci aspettiamo cioè che la
grandezza:
z = y - (A+Bx)
sia distribuita normalmente, abbia media nulla, e abbia una
varianza z = y
Il metodo per determinare A e B si basa ancora sulla proprietà
che la probabilità di osservare quel dato insieme di N misure sia
massima. Ciò corrisponde a minimizzare (rispetto ad A e B) la
grandezza:
N
2 = i=1 [yi - (A + B xi)]2
Si ottengono cosi' due equazioni in due incognite le cui
soluzioni sono:
N x2 N y N x N x y
i1 i i1 i i1 i i1 i i
A
N
N
N i1 xi y i i1 x i
B
y
N
i 1
2
N
N
N i 1 x i i 1 x i
2
i
25
La retta y = (A+Bx) basata sulle coppie di punti misurati (xi ,yi)
si chiama retta dei minimi quadrati, o retta di regressione
26
Stima degli errori per la retta di regressione
Le N misure yi non sono misure della stessa variabile.
Dipendono, infatti, da xi . Quindi ci si aspetta che sia la
grandezza
z = y - (A+Bx)
a distribuirsi in modo gaussiano, con varianza z = y
Al solito, la miglior stima di y è la grandezza
2
N
1
Sy
yi A B xi
( N 2) 1
Attenzione: nella espressione compare un N-2 al denominatore.
La dimostrazione di ciò è piuttosto complessa. E' semplice però
ricordarlo perché per due punti passa una retta; i gradi di libertà
del problema sono diminuiti di due unità!
Poiché nella retta di regressione determiniamo A e B, occorre
stimare il loro errore. La varianza di A e B dipende da y e si
ottiene (al solito) minimizzando il chi quadro. Si ottiene:
2
x
A2 y2 i
1
N
B2
N y2
27
Un esempio: (da Taylor, p.130)
Per un gas perfetto che si espande a volume costante:
T=a+bP
ove T è la temperatura del gas (misurata) in funzione di alcuni
valori di pressione P, anch'essi misurati con incertezza
trascurabile
Supponiamo che siano state fatte 5 misure di T in
corrispondenza di altrettanti valori di P
Prova Pi (mm hg)
Ti (oC)
a+bPi
[Ti-(a+bPi)]2
1
65
-20
-22.2
4.84
2
75
17
14.9
4.41
3
85
42
52.0
100.
4
95
94
89.1
24.0
5
105
127
126.2
0.64
n.b. le colonne 4 e 5 possono essere riempite solo dopo aver
determinato i parametri a e b
Dobbiamo:
1. determinare i parametri a e b
2. stimare la dispersione delle misure
3. stimare l'errore sui parametri a e b
Con l'ausilio di una calcolatrice, determiniamo le grandezze che
ci occorrono per stimare i parametri della retta di regressione:
Pi=425 ; P2i=37125 ; Ti=260; TiPi=25810 ;
da cui:
o
a = -263.35
C
o
b = 3.71
C/(mm hg)
= 5000
28
Possiamo calcolare la dispersione delle misure, sommando
l'ultima colonna della tabella e dividendo per (N-2)=3
o
T = (134/3) = 6.7
C
La varianza sulla temperatura è una stima della precisione
della misura della stessa grandezza. Quindi, la precisione
sulla determinazione di T è di circa 7 gradi centigradi.
Ora possiamo determinare gli errori sui parametri a e b della
correlazione lineare:
2a = 2T ( P2i) / = 331
a = 18 oC
e
2b = N2T / = 0.045
o
b = 0.21
C/(mm hg)
Possiamo quindi esprimere il risultato come:
a = (-260 20 )
o
b = ( 3.7 0.2 )
o
C
C/(mm hg)
Si noti che, entro l'errore, il valore di a è compatibile con il
valore T0= -273 oC
Si noti inoltre che l'incertezza di circa 7 oC nella regione
della misura si è propagata sino a diventare 20 oC.
La stessa cosa può essere qualitativamente ottenuta col
metodo grafico, in cui si tracciano le rette di massima e
minima pendenza compatibili con gli errori
29
Esperimento Pressione/ Temperatura (I)
Rappresentazione grafica dei dati in tabella.
La retta rappresentata è quella ottenuta dal fit.
Il grafico è stato realizzato con PAW (vedi appendice)
I parametri del fit possono anch'essi essere ottenuti con PAW
30
Esperimento Pressione/ Temperatura (II)
Gli stessi dati del grafico precedente, ma su una scala
espansa
31
Linearizzazione di una funzione esponenziale
Accade spesso che una legge fisica sia descritta da una
funzione esponenziale del tipo:
.
N(x) = No exp(-x)
.
Questo accade ad esempio nella legge del decadimento
radioattivo, o nell'esperienza del contatore Geiger
In quest'ultimo caso, si misurano i conteggi nell'unità di
tempo N(x) (conteggi/sec) registrati dal contatore in
funzione dello spessore x (cm) di materiale assorbitore
frapposto tra la sorgente radioattiva ed il Geiger. No è la
frequenza di conteggi in mancanza si materiale, e (cm-1) è
la costante che si deve determinare.
La legge può essere linearizzata nel modo:
lnN(x) = lnNo - x
y
= A+Bx
In questo modo, per determinare B = - si utilizzano le
formule note per la retta. Inoltre, può essere stimato l'errore
nella misura della variabile y .
32
La distribuzione binomiale
Talvolta, occorre risolvere problemi del tipo: "qual è la
probabilità di ottenere tre 6 lanciando tre dadi? E la
probabilità di ottenere due 6?"
A questo tipo di problema risponde la distribuzione
binomiale
TERMINOLOGIA:
Supponiamo di effettuare "n prove" (ossia, lanci di dadi,
monete…).
Ciascuna prova può avere varie uscite, di cui una (o una
combinazione) è il nostro successo . Ad es., l'uscita del 6.
Il successo ha una probabilità p di verificarsi. Nel nostro
caso, p(6 nei dadi) = 1/6.
L'insuccesso (= non successo) ha probabilità q=(1-p)
(nel nostro caso, q =5/6)
La probabilità di ottenere v successi in n prove è:
P( in n prove)
n (n 1) (n 1) n
p q
1 2
ossia, in altre notazioni
n n
n!
n
P( | n)
p q p q
!(n 1)!
33
Ad esempio, la probabilità di "due 6 su tre dadi" è:
P(due 6 su tre dadi) = 3!/2! (1/6)2 (5/6) = 3 0.0277 0.83 = 0.069 ~7%
Esempio 1: lancio di 4 monete. Qual è la probabilità di
ottenere 0,1,2,3,4 teste?
Esempio 2: un ospedale ricovera 4 malati, con una malattia la
cui mortalità è (dopo un mese) dell'80%. Calcolare la
probabilità che 0,1,2,3,4 malati sopravvivano dopo un mese.
Proprietà della distribuzione binomiale:
La distribuzione binomiale è una distribuzione discreta
(ossia, può assumere un numero finito di valori). Si può
calcolare il valor medio e la varianza di questa distribuzione:
Valor medio = <v> = n p
Varianza
= v = n p(1-p)
Nota: se il numero delle prove è grande (>30), per un valore
fissato della probabilità p la distribuzione binomiale viene
approssimata dalla distribuzione di Gauss con media X= n p e
varianza n p(1-p)
34
Distribuzione di Poisson
La distribuzione di Poisson e’ una nuova distribuzione
statistica che si applica per eventi casuali, ma con media
temporale definita .
Esempio: una sostanza radioattiva ha una certa attività’
decadimenti/secondo). Facendo n misure di 1 minuto, quale
distribuzione di conteggi ci dobbiamo aspettare?
P( v conteggi in t) =
e
P( )
!
Nella figura (pag. successiva) vengono presentate tre curve
per tre valori di (= 0.8 , 3 , 11 conteggi/s).
La distribuzione di Poisson può essere utilizzata in molti casi
( ad es. , la fig. 2 può adattarsi anche alla quantita’ di pasta
venduta da un ipermercato, la cui vendita media e’ di 3
quintali di pasta al giorno).
Proprieta’ della distribuzione di Poisson
Valore medio: <v> =
Varianza :
=
35
36
Queste formule sono molto importanti in pratica. Supponiamo
di aver effettuato una certa misura: ad esempio, di aver misurato
in un rivelatore, 202 interazioni in 4.2 anni di osservazione
dovute a rare interazioni di particelle presenti nei Raggi
Cosmici. L’errore che può essere associato a questa misura e’
proprio 202 , poiche’ in numero di eventi attesi segue la
statistica di Poisson.
In generale, quando si effettua una misura di v conteggi in un
dato periodo di osservazione, il “valor medio” della misura
coincide con la misura stessa, e l’errore associato pari alla v :
Stima conteggi = v v
Esercizio: il numero medio di disintegrazioni di un certo
campione radioattivo e’ 20/minuto. Quanto tempo occorre
aspettare per una misura precisa al 3% ? E all’1%?
37
Il test del 2
Ossia: come prendere una decisione
In precedenza, abbiamo conosciuto tre distribuzioni di
probabilità (Gauss, Binomiale, Poisson).
Abbiamo visto come stimare i parametri che adattano i dati
ad una retta (ed e’ facile estrapolare al caso di una qualunque
polinomiale).
Come e’ possibile stimare se i dati si adattano meglio ad una
curva, piuttosto che all’altra?
Per questo, esiste un criterio : il test del chi quadro ( 2).
Supponiamo di avere una serie di N misure yk di una
grandezza osservabile y, con varianza Sy. Riteniamo che la
grandezza y sia in accordo con una legge fisica del tipo f(xk)
yk= f(xk)
.
Nel caso ideale, in cui non esistano errori: yk - f(xk) = 0
Poiche’ ci sono le indeterminazioni, quello che ci aspettiamo e’
qualcosa del tipo:
(yk y)- f(xk) = 0
[(yk - f(xk) ]2 / y2 = 1
Sommando su tutte le N misure:
k [(yk - f(xk) ]2 / y2 = N
38
La grandezza “chi quadro” viene definita come:
2 = k [(yk - f(xk) ]2 / y2
In generale, ci si aspetta che il valore atteso per la grandezza chi
quadro per un insieme di N osservazioni coincide con N, ossia che
2 / N ~ 1. (chi quadro ridotto)
Un numero ‘troppo grande’ per il chi quadro significa che i
nostri dati non sono in accordo, entro gli errori, con i valori
attesi.
La grandezza chi quadro segue una propria funzione di
probabilita’ (la funzione chi quadro) la cui descrizione esula
dagli scopi del corso. Ciononostante, e’ relativamente semplice
utilizzarla seguendo le seguenti indicazioni:
1. Calcolare il 2 utilizzando la definizione.
2. Dividere per il “numero dei gradi di libertà” (coincide con il
numero di osservazioni se le predizioni sono note, e non sono
state ricavate con adattamenti (fit). Altrimenti, in numero dei
gradi di liberta’ e’ N-numero dei parametri del fit)
3. Se 2 >> 1, il risultato non e’ soddisfacente, se 2 1
l’accordo e’ soddisfacente.
4. Per un confronto piu’ quantitativo, utilizzare le tabelle nei
libri. Ad esempio, per 1, 5 e 10 gradi di liberta’:
P(2 1.0)
P(2 2.0)
P(2 3.0)
d=1
32%
16%
8.3%
d =5
42%
7.5 %
1.0%
d = 10
44%
2.9%
0.1%
39
Un esempio applicato alla distribuzione di Poisson
In un esperimento, si effettuano 100 misure della durata di un
minuto. Ciascuna misura, consiste nel contare il numero di
Raggi Cosmici rivelati da un contatore Geiger. La distribuzione
dei conteggi/min e’ riportata nella prima colonna.
Frequenza
di conteggi
0
1
2
3
4
5
6
7
>7
Occorrenza
Attesa ak
yk
poissoniana
7
7.5
17
19.4
29
25.2
20
21.7
16
14.1
8
7.4
1
3.1
2
1.2
0
0.4
Errore dk
su attesa
2.7
4.4
5.0
4.7
3.7
2.7
1.7
1.1
0.6
[(yk -ak)/dk]2
0.03
0.3
0.9
0.13
0.3
0.05
1.5
0.5
0.4
Stima del valor medio: v = 2.59
Da v ,con la funzione di Poisson, si ottengono i valori di
probabilita’ attesi per 0,1…7 occorrenze, e l’errore.
Il chi quadro e’ 3.8 per (9-1) gradi di liberta’. C’e’ infatti da
tener conto che con I dati abbiamo calcolato il valor medio v.
Il chi quadro ridotto e’ 3.8/8 = 0.48
I dati effettivamente si adattano alla distribuzione di Poisson.