LE FUNZIONI
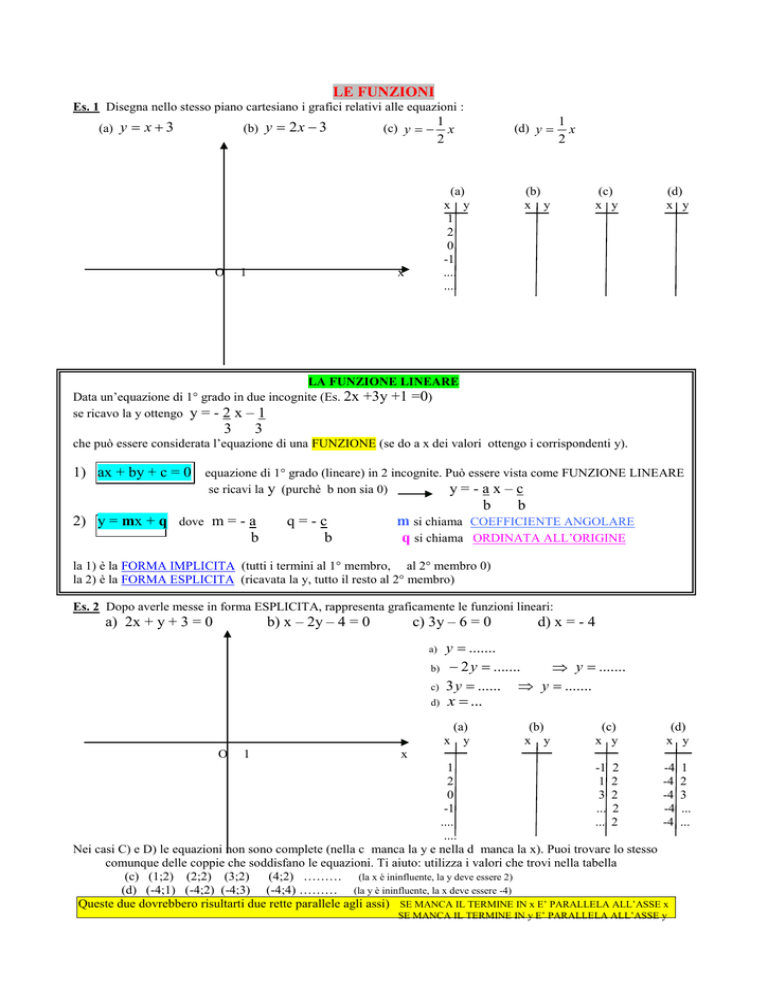
Es. 1 Disegna nello stesso piano cartesiano i grafici relativi alle equazioni :
(a) y x 3
(b) y 2 x 3
O
1
(c) y
1
x
2
(a)
x y
1
2
0
-1
....
....
x
(d) y
(b)
x y
1
x
2
(c)
x y
(d)
x y
LA FUNZIONE LINEARE
Data un’equazione di 1° grado in due incognite (Es. 2x +3y +1 =0)
se ricavo la y ottengo y = - 2 x – 1
3
3
che può essere considerata l’equazione di una FUNZIONE (se do a x dei valori ottengo i corrispondenti y).
1) ax + by + c = 0 equazione di 1° grado (lineare) in 2 incognite. Può essere vista come FUNZIONE LINEARE
se ricavi la y (purchè b non sia 0)
y=-ax–c
b
b
2) y = mx + q dove m = - a
q=-c
m si chiama COEFFICIENTE ANGOLARE
b
b
q si chiama ORDINATA ALL’ORIGINE
la 1) è la FORMA IMPLICITA (tutti i termini al 1° membro, al 2° membro 0)
la 2) è la FORMA ESPLICITA (ricavata la y, tutto il resto al 2° membro)
Es. 2 Dopo averle messe in forma ESPLICITA, rappresenta graficamente le funzioni lineari:
b) x – 2y – 4 = 0
a) 2x + y + 3 = 0
c) 3y – 6 = 0
a)
b)
c)
d)
y .......
2 y .......
y .......
3 y ...... y .......
x ...
x
O
1
d) x = - 4
(a)
y
(b)
x y
(c)
x y
(d)
x y
x
1
-1 2
-4
2
1 2
-4
0
3 2
-4
-1
... 2
-4
....
... 2
-4
....
Nei casi C) e D) le equazioni non sono complete (nella c manca la y e nella d manca la x). Puoi trovare lo stesso
comunque delle coppie che soddisfano le equazioni. Ti aiuto: utilizza i valori che trovi nella tabella
(c) (1;2) (2;2) (3;2)
(4;2) ……… (la x è ininfluente, la y deve essere 2)
(d) (-4;1) (-4;2) (-4;3) (-4;4) ……… (la y è ininfluente, la x deve essere -4)
Queste due dovrebbero risultarti due rette parallele agli assi) SE MANCA IL TERMINE IN x E’ PARALLELA ALL’ASSE x
SE MANCA IL TERMINE IN y E’ PARALLELA ALL’ASSE y
1
2
3
...
...
Es. 3
Sul quaderno a quadretti disegna i seguenti punti :
A(1;1)
Spostati di 2 quadretti verso destra e di 3 verso l’alto
Partendo da B fai gli stessi spostamenti
partendo da C fai gli stessi spostamenti
partendo da D fai gli stessi spostamenti
Congiungi tutti i punti.
Hai ottenuto una RETTA ?
Ripeti lo stesso esercizio partendo, invece che da A, dal punto H
Come risultano le rette? …………………………………..
CHIAMIAMO
x lo spostamento in ORIZZONTALE
CHIAMIAMO y lo spostamento in
B(….;…..)
C(…..;.....)
D(….;….)
E(….;.....)
(0;3)
+ se verso DESTRA
+
se verso SINISTRA
se verso L’ALTO
-
se verso il BASSO
VERTICALE
y
e risulta essere uguale al COEFFICIENTE ANGOLARE
x
y y B y A
PENDENZA
m
x x B x A
In una retta, si chiama PENDENZA il rapporto
PENDENZA o COEFFICIENTE ANGOLARE della retta è il rapporto costante
cioè
m
spostamento verticale
spostamento orizzontale
yB y A
di due qualsiasi punti A e B della retta
xB x A
Due rette PARALLELE hanno la stessa pendenza e quindi lo stesso
coefficiente angolare
Disegna una retta perpendicolare alle rette disegnate prima. Sai determinare dal grafico la sua PENDENZA?
Cosa osservi?
Due rette PERPENDICOLARI hanno le PENDENZE che sono una l’opposto e inverso dell’altra. Cioè hanno
prodotto = - 1.
Es. 4 Trova la PENDENZA
y
3
O
1
x
y …….
Scegli come punto iniziale
un punto qualsiasi e trova
gli spostamenti necessari
per giungere ad altri punti
x ……..
m
y
y 1 (verso il basso)
3
O
-1
y
…….
x
x
x 3
y ….
1
m ……
O
x
x ….
m ….
-3
In questi ultimi due casi la PENDENZA è NEGATIVA perché è il rapporto tra due numeri discordi ( y è negativa
(verso il basso) e
x positiva (verso destra))
Retta (a)
(a)
A
B
D
da A a B lo spostamento Verticale è = 0
Lo spostamento Orizzontale è = 1
m
O
1
C
y 0
0
x 1
m ……..
x
Retta (b)
m
(b)
da C a D lo spostamento Verticale è = 1
Lo spostamento Orizzontale è = 0
y 1
non esiste
x 0
m non c’è
RIASSUMENDO
RETTA
m
COEFFICIENTE ANGOLARE
Ascendente
POSITIVO
Discendente
NEGATIVO
y mx q
Eq retta
0
Orizzontale
Verticale
m e
eq. retta verticale
(vedi Es. 1)
Nell’equazione della FUNZIONE LINEARE
sono numeri
y 0 x q (manca termine x)
eq. retta orizzontale
NON ESISTE
q
xk
(manca termine y)
y mx q abbiamo visto che m rappresenta la
PENDENZA
e si chiama COEFFICIENTE ANGOLARE
Cosa rappresenta
q ? che si chiama
Es. 5
Rappresenta le rette di equazione:
ORDINATA ALL’ORIGINE
a) y 2 x
b) y 2 x 3
c) y 2 x 2
(a)
x y
-2
-1
0
1
O
1
d) y 2 x 4
(b)
x y
-2
-1
0
1
(c)
x y
-1
0
1
2
(d)
x y
0
1
2
3
x
Se osservi i grafici delle rette, ognuna di esse
interseca l’asse y proprio nel punto q
q
è quindi l’ordinata del punto in cui la retta incrocia l’asse y
y
y
q
O
Se q= 0 la retta
passa per l’Origine
x
O
x
Es. 6 Sul quaderno
Rappresenta le rette che passano per l’Origine e la cui pendenza è individuata dagli spostamenti indicati:
m
y 1
y .....x
(a)
equazione di (a)
x 1
(b)
x 4
y 5
equazione di (b)
y =...........
(c)
x 3
y 4
equazione di (c)
…………..
Es. 7 Sul quaderno
Rappresenta le rette che hanno coefficiente angolare
m e incrociano l’asse y nel punto P indicato:
P(0;2)
equazione
…………………………..
m = 4 incrocia asse y nel punto P(0;-1)
3
(f) m = 2 incrocia asse y nel punto P(0;3)
equazione
…………………………..
equazione
…………………………..
(d)
m = -3
incrocia asse y nel punto
(e)
LE FUNZIONI
Rappresenta graficamente le equazioni:
a) 2x + y = 0
b) y = 1
c) y = -x + 1
x
Es. 8
d) y – x = 3
e) y = x²
Una equazione in due incognite ha infinite soluzioni che sono rappresentabili sul piano cartesiano dai punti di una
curva (detta DIAGRAMMA o GRAFICO) : una retta, una parabola, una iperbole….
Se l’equazione è di 1° grado il diagramma è una RETTA
DIAGRAMMA o GRAFICO : insieme dei punti del piano le cui coordinate soddisfano l’equazione, cioè la rendono
VERA
Nei casi
b) c) e) è stato facile trovare le coppie (x;y) perché bastava dare un valore a x per trovare subito y
FUNZIONE
tra due insiemi di valori
x
y
è la corrispondenza che lega due VARIABILI (x;y) in modo tale che dato un valore alla prima (x =
variabile indipendente ) ESISTE UNO e UN SOLO valore della seconda ( y = variabile dipendente).
DOMINIO della funzione : è l’insieme dei valori che si possono dare a x perché esista y
Es: nella corrispondenza y = 1 non possiamo dare a x valore 0 perché 1 non esiste. Quindi il DOMINIO contiene tutti i
numeri tranne 0
x
0
CODOMINIO della funzione : è l’insieme dei valori che assume la y al variare di x (cioè tutti i risultati che otteniamo
dando a x dei valori)











