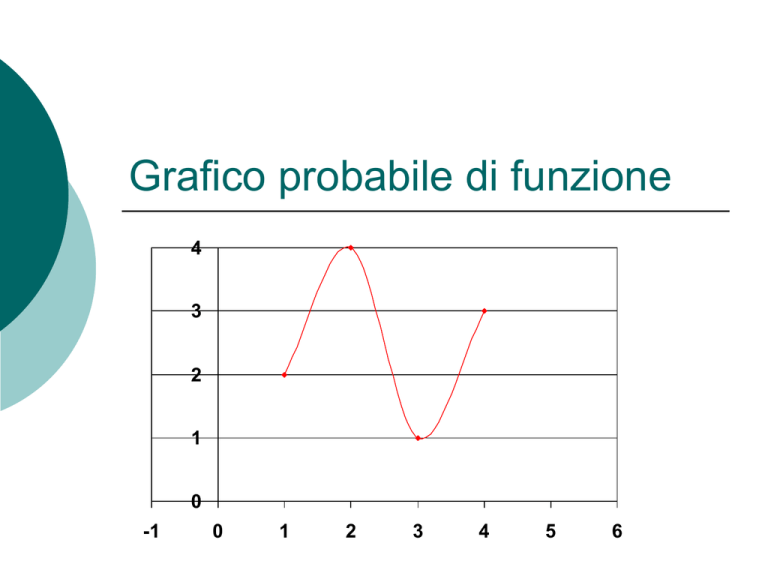
Grafico probabile di funzione
4
3
2
1
0
-1
0
1
2
3
4
5
6
Sia
Dominio
x
f ( x) y
4
x2 4x 3
2
la funzione di cui devo calcolare il dominio
ac
La funzione è definita per tutti i valori reali eccetto quelli che annullano il
2
denominatore devo quindi escludere le soluzioni dell’equazione 1x 4 x 3 0
-b/2 (-b/2)2
3
x1, 2 2 4 3
Uso la formula ridotta
D 1;3 (;1) (1;3) (3; )
y
1
-2
Traccio gli assi e alcuni
punti di riferimento
-1
0
-1
1
2
3
x
1
Intersezione con gli assi
x2 4
La funzione f ( x) y 2
Interseca l’asse y quando x=0 cioè
x 4x 3
04
4
y
003
3
x 2 4 0 x 2
Interseca l’asse x quando y=0 cioè
y
1
B
-2
-1
0
-1
A -4/3
1
C
2
3
x
Segno della funzione
x 4
2
è positiva quando numeratore e denominatore
x 4 x 3 sono concordi
per valori esterni alle 2
Studio il segno del numeratore x 2 4 è 0
radici dell’equazione x 4 0 x 2
cioè x<-2 e x>2
per valori esterni alle 2
2
x 4x 3 0
x
4
x
3
è
0
il segno del denominatore
radici dell’equazione
La funzione
f ( x) y
2
x1, 2 1 3
cioè x 1 x 3
per cui il loro rapporto è >0 per x<-2 per 1<x<2
e per x>3
<0 per -2<x<1 e 2<x<3
y
N/D
D
N
1
-2
-1
1
-1
2
3
0
-2
1
x
2
3
Limiti della funzionex
Calcolo i limiti della funzione f ( x) y
4
x 2 4 x 3
2
4
2
x
1
2
2
x 4
x 1
lim 2
lim
x x 4 x 3
x
4 3
x 2 1 2
x x
Vi è quindi un asintoto orizzontale
y=1
x=1
x=3
y
Ai suoi estremi di definizione
(in questo caso ±∞) e nei suoi
punti singolari (1 e 3)
2
lim x 4 1 4
x1 x 2 4 x 3 1,... 4 3
x2 4
1 4
lim
x1 x 2 4 x 3 0,999 4 3
2
94
lim x 4
x3 x 2 4 x 3 9,... 12 3
2
94
lim x 4
x3 x 2 4 x 3 8,999 12 3
Vi sono quindi 2 asintoti verticali
x=1 e x=3
Il punto d’incontro del
grafico con l’asintoto
x
orizzontale è dato dal
sistema
y 1
7
2
cioè
D
,1
x 4
4
y 2
x 4x 3
y=1
(-7/4;1)
1
-2
-1
1
-1
2
3
0
Grafico della funzione
x2 4
f ( x) y 2
x 4x 3
Traccio quindi il grafico della funzione
Tenendo conto dei limiti e dei
punti trovati
x=1
y
x=3
y=1
1
B
-2
-1
D
O
-1
A -4/3
1
(-7/4;1)
C
2
3
0
x
Dominio
f ( x) y
x2 2x 3
Sia
la funzione di cui devo calcolare il dominio
x2
La funzione è definita per tutti i valori reali eccetto quelli che annullano il
ac
denominatore e che rendono negativo l’argomento della radice
2
1
x
2x 3 0
devo quindi escludere x=2 e i valori interni agli zeri dell’equazione
-b/2 (-b/2)2
Uso la formula ridotta
1
D 2 (3;1) (;3] [1;2) (2; )
x1, 2 1 1 3
y
1
-3
-2
Traccio gli assi e alcuni
punti di riferimento
-1
0
-1
1
2
3
x
3
Intersezione con gli assi
La funzione f ( x) y
x2 2x 3
Non può Intersecare l’asse y in quanto x
x2
non può essere 0
x 2 2 x 3 0 x1 3 x2 1
Interseca l’asse x quando y=0 cioè
y
1
A
-3
-2
-1
0
-1
B
1
2
3
x












