LABORATORIO DI TECNICHE COMPUTAZIONALI IN BIOLOGIA
Soluzioni Prova di Laboratorio MAT 1 A.A.2004/2005
Problema 1:
Si consideri l’esperienza del lancio di due dadi regolari a 6 facce. Si indichi con X1 il risultato del
lancio del primo dado e con X2 il risultato del lancio del secondo dado. Sia Y = X1+X2 la
variabile aleatoria somma delle uscite, che prende valore nell’intervallo [2,12].
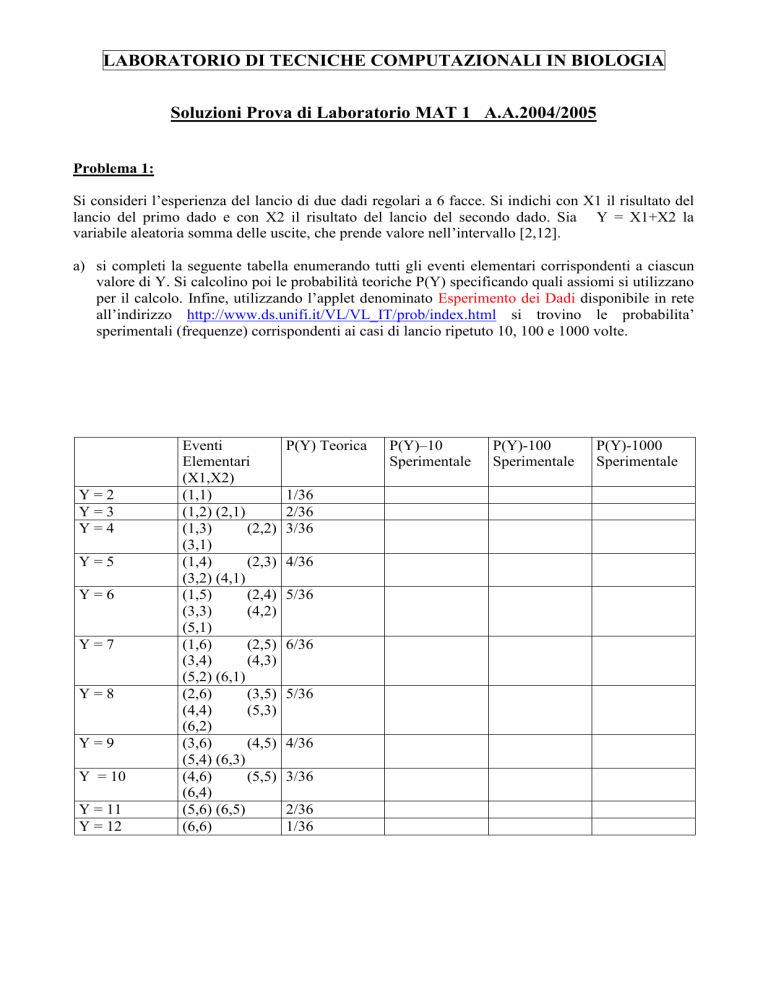
a) si completi la seguente tabella enumerando tutti gli eventi elementari corrispondenti a ciascun
valore di Y. Si calcolino poi le probabilità teoriche P(Y) specificando quali assiomi si utilizzano
per il calcolo. Infine, utilizzando l’applet denominato Esperimento dei Dadi disponibile in rete
all’indirizzo http://www.ds.unifi.it/VL/VL_IT/prob/index.html si trovino le probabilita’
sperimentali (frequenze) corrispondenti ai casi di lancio ripetuto 10, 100 e 1000 volte.
Y=2
Y=3
Y=4
Y=5
Y=6
Y=7
Y=8
Y=9
Y = 10
Y = 11
Y = 12
Eventi
Elementari
(X1,X2)
(1,1)
(1,2) (2,1)
(1,3)
(2,2)
(3,1)
(1,4)
(2,3)
(3,2) (4,1)
(1,5)
(2,4)
(3,3)
(4,2)
(5,1)
(1,6)
(2,5)
(3,4)
(4,3)
(5,2) (6,1)
(2,6)
(3,5)
(4,4)
(5,3)
(6,2)
(3,6)
(4,5)
(5,4) (6,3)
(4,6)
(5,5)
(6,4)
(5,6) (6,5)
(6,6)
P(Y) Teorica
1/36
2/36
3/36
4/36
5/36
6/36
5/36
4/36
3/36
2/36
1/36
P(Y)–10
Sperimentale
P(Y)-100
Sperimentale
P(Y)-1000
Sperimentale
b) Si commenti la discrepanza fra la probabilità teorica e le tre probabilità stimate
Utilizzando l’applet si dovrebbe aver osservato che la discrepanza fra probabilità teorica e
frequenza sperimentale cala al crescere del numero di lanci. Questo a causa della “legge dei grandi
numeri”.
c) Si calcoli la probabilità teorica e quella stimata usando l’esperienza con la ripetizione del lancio
1000 volte dei seguenti eventi:
1. Y e’ minore o uguale di 5
2. Y e’ compresa nell’intervallo [8,10]
P(Y minore o uguale a 5) = P(Y=2) + P(Y=3) + P(Y=4) + P(Y=5)
= (1+2+3+4)/36 = 10/36
P(Y compresa nell’intervallo [8,10]) = P(Y=8) + P(Y=9) +P(Y=10)
= (5+4+3)/36 = 12/36
Problema 2:
a) Una pallina è estratta in modo casuale da un’urna che contiene 6 palline rosse, 4 bianche e 5
azzurre. Qual è la probabilità di estrarre una pallina rossa? Qual è la probabilità di estrarre una
pallina rossa o bianca? Motivare la risposta.
La probabilità di estrarre una pallina rossa è : 6/15
La probabilità di estrarre una pallina rossa o bianca è: 10/15
b) Si deve costituire un comitato di tre studenti universitari, rappresentanti ciascuno gli studenti del
I anno, quelli del II anno e quelli del III anno. Supponendo che ci siano 5 candidati per gli studenti
del I anno, 3 candidati per quelli del II anno, 6 candidati per quelli del terzo anno, si determini
quanti comitati differenti si possono formare. Motivare la risposta.
Il numero di differenti comitati che si possono formare è: 5x3x6 = 90
c) Si estrae a caso una carta da un mazzo di 52 carte. Qual è la probabilità di estrarre un dieci o una
carta di picche? Motivare la risposta.
La probabilità di estrarre un dieci o una carta di picche è: (13+3)/52 = 16/52