1
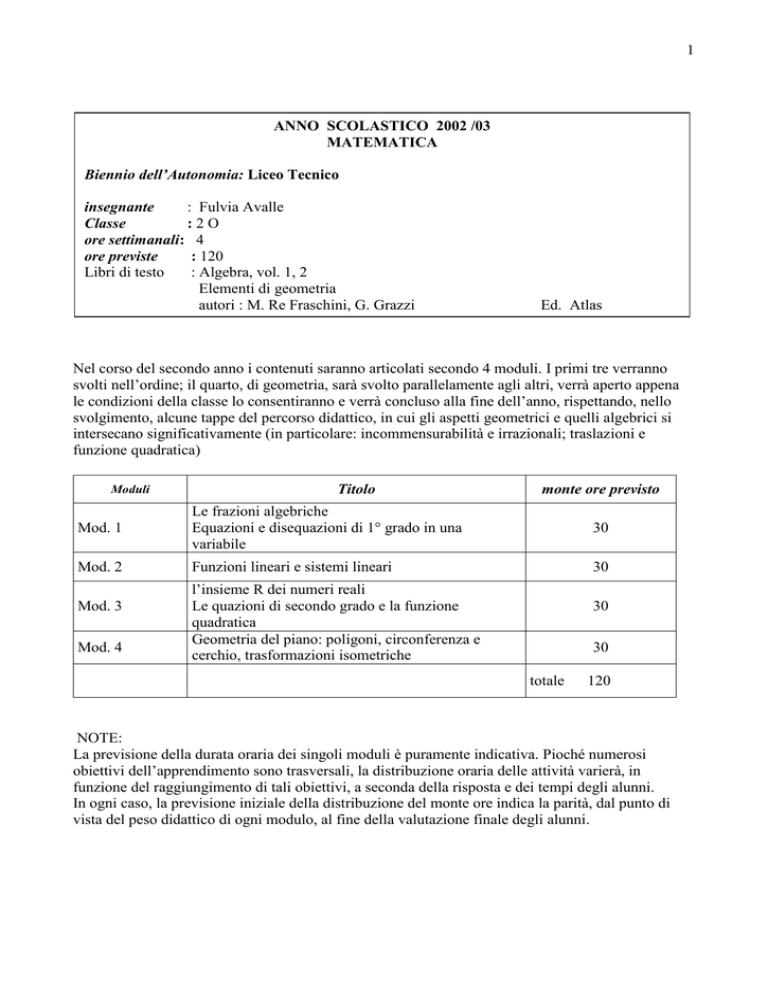
ANNO SCOLASTICO 2002 /03
MATEMATICA
Biennio dell’Autonomia: Liceo Tecnico
insegnante
: Fulvia Avalle
Classe
:2O
ore settimanali: 4
ore previste
: 120
Libri di testo
: Algebra, vol. 1, 2
Elementi di geometria
autori : M. Re Fraschini, G. Grazzi
Ed. Atlas
Nel corso del secondo anno i contenuti saranno articolati secondo 4 moduli. I primi tre verranno
svolti nell’ordine; il quarto, di geometria, sarà svolto parallelamente agli altri, verrà aperto appena
le condizioni della classe lo consentiranno e verrà concluso alla fine dell’anno, rispettando, nello
svolgimento, alcune tappe del percorso didattico, in cui gli aspetti geometrici e quelli algebrici si
intersecano significativamente (in particolare: incommensurabilità e irrazionali; traslazioni e
funzione quadratica)
Moduli
Titolo
monte ore previsto
Mod. 1
Le frazioni algebriche
Equazioni e disequazioni di 1° grado in una
variabile
30
Mod. 2
Funzioni lineari e sistemi lineari
30
Mod. 3
Mod. 4
l’insieme R dei numeri reali
Le quazioni di secondo grado e la funzione
quadratica
Geometria del piano: poligoni, circonferenza e
cerchio, trasformazioni isometriche
30
30
totale
120
NOTE:
La previsione della durata oraria dei singoli moduli è puramente indicativa. Pioché numerosi
obiettivi dell’apprendimento sono trasversali, la distribuzione oraria delle attività varierà, in
funzione del raggiungimento di tali obiettivi, a seconda della risposta e dei tempi degli alunni.
In ogni caso, la previsione iniziale della distribuzione del monte ore indica la parità, dal punto di
vista del peso didattico di ogni modulo, al fine della valutazione finale degli alunni.
2
METODOLOGIA
Lezioni frontali
Lezioni dialogate
Esercitazioni individuali
Esercitazioni a piccoli gruppi
Discussioni guidate
Attività di laboratorio
STRUMENTI
Libro di testo
Software didattico: Derive, Cabri-geomètre
Schede di lavoro preparate dall’insegnante
Eventuali letture di carattere matematico e interdisciplinare
Eventuale consultazione di siti Internet di matematica
MODALITA’ DI VERIFICA
Verifiche scritte e orali, generali e a campione, individuali e di gruppo, in ogni momento del
percorso didattico, su conoscenze e competenze limitate, al fine di monitorare il livello di
comprensione e la qualità dell’impegno degli alunni, anche all’interno di ogni unità.
Verifiche di unità
Verifiche di modulo
Verifiche di recupero di modulo
La valutazione delle verifiche intermedie contribuirà per non meno del 40% e non più
del 50% sulla valutazione finale del modulo.
CRITERI PER LA MISURAZIONE dei LIVELLI DI PRESTAZIONE RAGGIUNTI
Sulla base dei livelli definiti dalla griglia di valutazione adottata dal nostro Istituto, le verifiche
scritte saranno valutate, secondo i livelli di CONOSCENZE, COMPETENZE e CAPACITA’.
In particolare, saranno proposti (non necessariamente tutti in ogni prova) quesiti finalizzati a
verificare :
le conoscenze dei contenuti, compreso l’utilizzo corretto del linguaggio specifico
le competenze necessarie ad applicare le conoscenze per conseguire risultati (in situazioni di
“esercizio” analoghe a quelle affrontate in classe)
le capacità acquisite nell’affrontare situazioni problematiche e individuare strategie
risolutive, scegliendo, tra gli strumenti concettuali e operativi a disposizione, quelli idonei.
Le verifiche orali avranno lo scopo di :
- stimolare la capacità di “parlare di matematica”, comunicando contenuti con
senso, in modo semplice ma corretto
- controllare la correttezza dei ragionamenti
3
CRITERI DI VALUTAZIONE
La valutazione delle prove segue la corrispondenza:
INSUFFICIENZA GRAVISSIMA ( 0-3 ): lo studente non ha conoscenze sugli argomenti trattati e
non è in grado di agire
INSUFFICIENZA GRAVE ( 4 ): ha conoscenze scarse e frammentarie, e commette significativi
errori nelle applicazioni
INSUFFICIENZA ( 5 ): ha conoscenze superficiali e commette errori nell’applicazione
SUFFICIENZA ( 6 ): ha conoscenze non approfondite, che esprime in modo abbastanza adeguato e
applica senza commettere gravi errori
DISCRETO ( 7 ): ha conoscenze che sa esporre ed applicare adeguatamente in ambiti predefiniti
BUONO ( 8 ): ha conoscenze approfondite che sa esporre con sicurezza e applicare adeguatamente
in ambiti diversi
OTTIMO (9-10 ): ha conoscenze approfondite, capacità di analisi e sintesi, è in grado di
organizzare le sue conoscenze in modo autonomo scegliendo opportunamente le procedure
adeguate alle situazioni.
ATTIVITA’ DI RECUPERO
Recupero di conoscenze e competenze irrinunciabili, relative al programma del primo anno,
all’interno del monte ore delle attività integrative.
(Quando occorre) recupero in itinere di conoscenze e competenze non acquisite o acquisite
in modo insufficiente dalla maggior parte degli alunni, attraverso attività di rinforzo,
esercitazioni, affronto degli stessi argomenti da punti di vista e con strumenti diversi
(Quando occorre) recupero pomeridiano extracurricolare di conoscenze e competenze non
acquisite o acquisite in modo insufficiente da una minoranza di alunni.
ATTIVITA’ DI APPROFONDIMENTO
Se si evidenziano condizioni favorevoli (in termini di impegno, interesse, partecipazione,
capacità), attività di approfondimento di argomenti affrontati in classe, o affronto di
argomenti extracurricolari, attraverso un lavoro guidato nelle premesse e nell’impostazione,
ma non nell’esecuzione, proposto agli alunni che non necessitano di attività di recupero.
4
MODULO 1
U. D. 1: IL LINGUAGGIO DELL’ALGEBRA (recupero e completamento del programma
dell’anno scorso – mod. 2 - )
CONTENUTI:
Algebra dei polinomi
Fattorizzazione di polinomi
Operazioni con le frazioni algebriche
COMPETENZE:
Riconoscere ed utilizzare il linguaggio dell’algebra per formalizzare
Interpretare e decodificare scritture simboliche
Applicare le proprietà e le regole del calcolo algebrico per operare con espressioni scritte in linguaggio
simbolico
DESCRITTORI: Operare con monomi e polinomi:somma algebrica, prodotti e potenze
Calcolare i prodotti notevoli
a b2 ; a b3 ; a ba b; a b c 2
Scomporre in fattori gli sviluppi dei prodotti notevoli , il trinomio particolare e i polinomi in
generale mediante raccoglimento totale e parziale.
Calcolare M.C.D. e m.c.m. tra monomi e polinomi.
Determinare il dominio di una frazione algebrica.
Semplificare una frazione algebrica.
Operare con frazioni algebriche.
Formalizzare espressioni e formule espresse in linguaggio naturale
Tradurre in linguaggio naturale espressioni e formule scritte in linguaggio algebrico.
U. D. 2: EQUAZIONI E DISEQUAZIONI DI PRIMO GRADO
CONTENUTI:
Equazioni e disequazioni.
Equazioni di primo grado intere e frazionarie, equazioni riconducibili al primo grado
Disequazioni intere di primo grado, sistemi di disequazioni di primo grado
COMPETENZE:
Riconoscere ed utilizzare il linguaggio dell’algebra per formalizzare proposizioni aperte
Interpretare e decodificare formule (equazioni, disequazioni)
Riconoscere modelli adeguati per formalizzare problemi
Utilizzare modelli adeguati per risolvere problemi
Discutere le soluzioni di un problema in funzione dell’obiettivo
DESCRITTORI: Determinare l’insieme delle soluzioni di un’equazione di primo grado in una incognita a
coefficienti numerici.
Determinare il dominio e l’insieme delle soluzioni di un’equazione numerica fratta.
Determinare l’insieme delle soluzioni di un’equazione di grado superiore al primo applicando la
legge d’annullamento del prodotto.
Risovere una disequazione di primo grado in una incognita e rappresentarne l’insieme delle
soluzioni
Risolvere e rappresentare l’insieme delle soluzioni di un sistema di disequazioni di primo grado in
una incognita in un dominio prefissato
Formalizzare e risolvere un problema con una disequazione o un sistema di disequazioni.
5
MODULO 2
U.D.1: FUNZIONI LINEARI E RAPPRESENTAZIONI GRAFICHE
CONTENUTI:
Il piano cartesiano
La retta nel piano cartesiano
La rappresentazione grafica delle radici di un’equazione di primo grado
La rappresentazione grafica dell’insieme delle soluzioni di un’equazione lineare in due variabili
La rappresentazione grafica dell’insieme delle soluzioni di una disequazione lineare in due variabili
COMPETENZE:
Riconoscere la corrispondenza tra insieme delle soluzioni di un’equazione o disequazione e la sua
rappresentazione grafica nel piano cartesiano
Riconoscere la corrispondenza tra equazioni lineari in due variabili e rette nel piano cartesiano
Tradurre modelli algebrici di primo grado in modelli geometrici e viceversa
Analizzare, impostare e risolvere problemi con metodi algebrici e grafici.
DESCRITTORI: Determinare il coefficiente angolare di una inclinazione.
Tracciare il grafico di una retta avente un assegnato coefficiente angolare.
Determinare l’equazione di una retta di cui è assegnato il grafico in un riferimento cartesiano.
Tracciare il grafico di una retta di cui è assegnata l’equazione, sia in forma esplicita che canonica.
Conoscere le condizioni analitiche di parallelismo e perpendicolarità tra rette.
Determinare l’equazione di una retta, assegnate due condizioni.
Interpretare graficamente una disequazione lineare in due variabili e rappresentarne l’insieme
delle soluzioni
Formalizzare e risolvere un problema con una disequazione in due variabili
U.D.2: SISTEMI LINEARI
CONTENUTI:
Sistemi di equazioni lineari in due variabili
Sistemi di disequazioni lineari in due variabili
COMPETENZE:
Risolvere e discutere sistemi numerici di equazioni e disequazioni con metodi algebrici e grafici, riconoscendo
la corrispondenza tra i due metodi
Tradurre modelli algebrici di primo grado in modelli geometrici e viceversa
Analizzare, impostare e risolvere problemi con più condizioni con metodi algebrici e grafici.
DESCRITTORI: Determinare l’insieme delle soluzioni di un sistema lineare di due equazioni in due incognite, sia
graficamente che con i metodi algebrici di sostituzione, confronto e riduzione.
Stabilire, in dipendenza del valore dei coefficienti, mediante l’interpretazione grafica, se un
sistema è determinato, indeterminato, impossibile.
Scrivere un sistema del quale sia assegnato l’insieme delle soluzioni.
Rappresentare graficamente l’insieme delle soluzioni di un sistema di disequazioni lineari
Formalizzare e risolvere un problema di primo grado con un sistema di equazioni o disequazioni
in due variabili
6
MODULO 3
U. D. 1: L’ INSIEME R DEI NUMERI REALI
CONTENUTI:
L’insieme dei numeri reali
La continuità e il problema della misura
Le potenze ad esponente razionale
I radicali
COMPETENZE:
Riconoscere numeri appartenenti ad insiemi diversi
Collegare gli aspetti algebrici e geometrici che portano all’ampliamento di Q
Affrontare e risolvere problemi di natura algebrica e geometrica che richiedono l’ampliamento dell’insieme Q
Operare con i radicali quadratici utilizzando teoremi e proprietà delle potenze
DESCRITTORI
Riconoscere e caratterizzare i numeri razionali e irrazionali.
Definire la radice n-esima di un numero reale
Definire la radice aritmetica n-esima di un numero reale non negativo
Definire una potenza ad esponente razionale
2
Utilizzare il valore assoluto per semplificare radicali del tipo a
Trasformare radicali quadratici (“portare dentro”, “portare fuori”)
Razionalizzare il denominatore di frazioni irrazionali.
Calcolare espressioni contenti radicali quadratici
Determinare il dominio di semplici funzioni irrazionali.
U.D.2: LE EQUAZIONI DI SECONDO GRADO
CONTENUTI:
Equazioni di secondo grado
Formula risolutiva per le equazioni complete di secondo grado
Condizioni per l’esistenza di radici reali delle equazioni di secondo grado
COMPETENZE:
Interpretare e decodificare formule
Distinguere in una formula il ruolo dei parametri da quello delle variabili
Tradurre in linguaggio algebrico e risolvere condizioni su variabili e parametri
Riconoscere modelli adeguati per formalizzare problemi di grado superiore al primo
Utilizzare modelli adeguati per risolvere problemi
Discutere le soluzioni di un problema in funzione dell’obiettivo
DESCRITTORI
Determinare l’insieme delle soluzioni di un’equazione di secondo grado incompleta (o
fattorizzabile) applicando la legge d’annullamento del prodotto.
Determinare l’insieme delle soluzioni di un’equazione di secondo grado completa applicando la
formula risolutiva (e la formula ridotta se b è pari).
Scrivere un’equazione avente l’insieme delle soluzioni assegnato.
Determinare il dominio e l’insieme delle soluzioni di un’equazione fratta avente eventualmente il
denominatore di secondo grado.
Determinare le caratteristiche dell’insieme delle soluzioni di un’equazione al variare del valore
dei coefficienti
Formalizzare e risolvere un problema di secondo grado
7
U.D. 3: LA FUNZIONE QUADRATICA
CONTENUTI:
La funzione quadratica
La rappresentazione della funzione quadratica nel piano cartesiano
L’interpretazione grafica delle radici di un’equazione di secondo grado
COMPETENZE:
Riconoscere la corrispondenza tra insieme delle soluzioni di un’equazione e la sua rappresentazione grafica nel
piano cartesiano
Riconoscere la corrispondenza tra funzioni quadratiche e parabole nel piano cartesiano
Tradurre modelli algebrici di secondo grado in modelli geometrici e viceversa
Analizzare, impostare, risolvere e discutere problemi di secondo gradocon metodi algebrici e grafici.
DESCRITTORI: Rappresentare graficamente la funzione y ax 2 ,al variare del valore di a.
2
Rappresentare graficamente la funzione y k a x h , al variare del valore di a, h, k.
2
Rappresentare la funzione y ax bx c , determinandone il vertice e le intersezioni con gli
assi.
Determinare l’equazione di una parabola di cui siano noti l’apertura a (oppure l’appartenenza di un
punto) e il vertice.
8
MODULO 4
U. D. 1: I POLIGONI, I POLIGONI REGOLARI, LA CIRCONFERENZA(recupero e
completamento del programma dell’anno scorso – mod. 3-)
CONTENUTI:
I triangoli rettangoli
I quadrilateri: parallelogrammi e trapezi
I poligoni regolari
La circonferenza e il cerchio
COMPETENZE:
Utilizzare correttamente il linguaggio della geometria per descrivere figure geometriche e loro proprietà
Eseguire correttamente disegni con gli strumenti opportuni, facendo corrispondere figure ed enunciati
Individuare ipotesi e tesi di un teorema
Comprendere la forma di una dimostrazione e la sua necessità logica
Calcolare perimetri e aree di poligoni e cerchi, utilizzando anche i numeri irrazionali
Applicare i teoremi di Euclide e il teorema di Pitagora nella loro forma algebrica
Utilizzare modelli algebrici per risolvere problemi geometrici
DESCRITTORI: Conoscere le proprietà dei triangoli rettangoli, dei parallelogrammi e dei trapezi
Conoscere le proprietà dei poligoni regolari
Conoscere le proprietà della circonferenza e delle sue parti
Conoscere le relazioni tra archi, corde, angoli al centro e alla circonferenza
Riconoscere lunghezze incommensurabili e utilizzare i numeri irrazionali per esprimerne la misura
Calcolare perimetri e aree delle figure studiate
Risolvere triangoli rettangoli particolari, utilizzando anche il teorema di Pitagora
Formalizzare con equazioni e risolvere problemi di geometria di primo e secondo grado
U.D.2: LE TRASFORMAZIONI ISOMETRICHE DEL PIANO
CONTENUTI:
Simmetrie assiali
Rotazioni e simmetria centrale
Traslazioni
COMPETENZE
Utilizzare il linguaggio delle trasformazioni per descrivere proprietà delle figure geometriche
Eseguire correttamente disegni con gli strumenti opportuni, facendo corrispondere figure ed enunciati
Formulare congetture sulle proprietà delle figure geometriche utilizzando le proprietà delle trasformazioni
DESCRITTORI: Riconoscere e costruire graficamente isometrie
Riconoscere proprietà isometriche di una figura
Definire le isometrie del piano e dedurne le proprietà
Riconoscere gli invarianti delle trasformazioni isometriche
Ricavare in casi semplici le equazioni cartesiane di una isometria
Utilizzare le equazioni delle traslazioni per scrivere l’equazione di una parabola avente il vertice in
(h,k)
L’insegnante: