Propagazione guidata

Propagazione guidata
Appendice al § 12.4.2 dello Sze
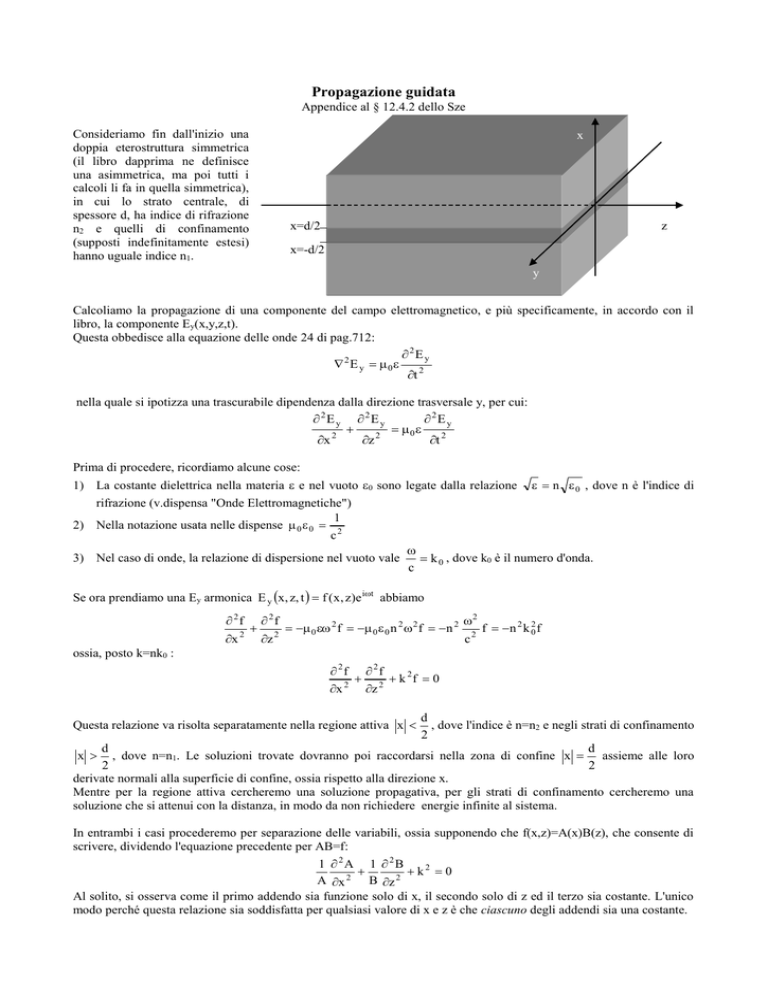
Consideriamo fin dall'inizio una
doppia eterostruttura simmetrica
(il libro dapprima ne definisce
una asimmetrica, ma poi tutti i
calcoli li fa in quella simmetrica),
in cui lo strato centrale, di
spessore d, ha indice di rifrazione
n2 e quelli di confinamento
(supposti indefinitamente estesi)
hanno uguale indice n1.
x
x=d/2
z
x=-d/2
y
Calcoliamo la propagazione di una componente del campo elettromagnetico, e più specificamente, in accordo con il
libro, la componente Ey(x,y,z,t).
Questa obbedisce alla equazione delle onde 24 di pag.712:
 2E y
2E y  0
t 2
nella quale si ipotizza una trascurabile dipendenza dalla direzione trasversale y, per cui:
 2E y  2E y
 2E y




0
x 2
z 2
t 2
Prima di procedere, ricordiamo alcune cose:
1) La costante dielettrica nella materia  e nel vuoto 0 sono legate dalla relazione
  n  0 , dove n è l'indice di
rifrazione (v.dispensa "Onde Elettromagnetiche")
1
2) Nella notazione usata nelle dispense  0  0  2
c
3) Nel caso di onde, la relazione di dispersione nel vuoto vale

 k 0 , dove k0 è il numero d'onda.
c
Se ora prendiamo una Ey armonica E y x, z, t   f ( x, z)e it abbiamo
 2f
x
2

 2f
z
2
  0  2 f   0  0 n 2  2 f  n 2
2
c
2
f  n 2 k 02 f
ossia, posto k=nk0 :
 2f
x 2

 2f
z 2
 k 2f  0
d
, dove l'indice è n=n2 e negli strati di confinamento
2
d
d
x  , dove n=n1. Le soluzioni trovate dovranno poi raccordarsi nella zona di confine x  assieme alle loro
2
2
derivate normali alla superficie di confine, ossia rispetto alla direzione x.
Mentre per la regione attiva cercheremo una soluzione propagativa, per gli strati di confinamento cercheremo una
soluzione che si attenui con la distanza, in modo da non richiedere energie infinite al sistema.
Questa relazione va risolta separatamente nella regione attiva x 
In entrambi i casi procederemo per separazione delle variabili, ossia supponendo che f(x,z)=A(x)B(z), che consente di
scrivere, dividendo l'equazione precedente per AB=f:
1  2A 1  2B

 k2  0
A x 2 B z 2
Al solito, si osserva come il primo addendo sia funzione solo di x, il secondo solo di z ed il terzo sia costante. L'unico
modo perché questa relazione sia soddisfatta per qualsiasi valore di x e z è che ciascuno degli addendi sia una costante.
Non si perde in generalità se si pone
1  2B
  2 , dove  è una costante, che porremo uguale a 1 negli strati di
B z 2
confinamento, ed uguale a 2 nella regione attiva. La soluzione di questa porzione di equazione è Bz  e iz . Delle
due possibilità si sceglie quella con il segno negativo perché così la forma della componente E y del campo assume già la
caratteristica di propagazione progressiva lungo z:
E y x, z, t   Ax e i t z 
Per quanto concerne A, la equazione risultante è
1  2A
 k 2  2  0
A x 2
che ha per soluzione
A( x )  a exp  i k 2   2 x   b exp   i k 2   2 x 




e se k2>2 questo corrisponde ad una soluzione oscillante, altrimenti le esponenziali diventano di argomento reale e
rappresentano una combinazione di una crescita e di una diminuzione esponenziale con il crescere della distanza.
Se nella regione attiva potremo scegliere la soluzione oscillante
A 2 ( x )  a exp  i k 22   22 x   b exp   i k 22   22 x  , che, per la simmetria del sistema potremo già scrivere come




A 2 ( x )  A 0 cos k 22   22 x 


per cui
E y 2 x, z, t   A 0 cos k 22   22 x ei t 2z 


negli strati di confinamento dovremo non solo scegliere l'altra forma, ma anche porre a zero il coefficiente del termine
esponenziale che cresce illimitatamente con la distanza:
A1 x    exp   12  k12 x 


per cui
E y1 x, z, t    exp   12  k12 x e it 1z 


dove il modulo di x serve ad garantire che anche nella regione delle x negative si abbia attenuazione al crescere della
distanza. Grazie alla simmetria ci potremo limitare a cercare le condizioni di raccordo solo in x=d/2.
Cominciando dalla condizione di raccordo delle funzioni E y1 e Ey2, abbiamo subito che

d
d

A 0 cos k 22   22 e i t 2z    exp   12  k 12 e i t 1z 
2
2



e questa relazione può essere possibile per qualsiasi valore di z solo se 1=2.
Abbiamo dunque, in x>0:
 E y1 x, z, t 

2
2  i t z 

   2  k 12  exp    2  k 12 x e i t z 

E y1 x, z, t    exp     k 1 x e


x
e quindi anche: 

E y 2 x, z, t 
2
2  i t z 

 E y 2 x, z, t   A 0 cos k 2   x e

  k 22   2 A 0 sen k 22   2 x e i t z 






x
La condizione di raccordo diviene dunque:


 exp    2  k 12




2
2
   k 1  exp    2  k 12



Dalla prima si esprime  come :
d  i t z 
d

 A 0 cos k 22   2 e i t z 
e
2
2

d  i t z 
d

  k 22   2 A 0 sen k 22   2 e i t z 
e
2
2

d
d


  A 0 cos k 22   2  exp   2  k12 
2
2



per cui:


d  i t z 
 2
2 d
2
2
 exp    k 1  x   e
E y1 x, z, t   A 0 cos k 2  
2
2 






2
2
i

t


z


E x, z, t   A cos k   x e
0
2
 y 2


mentre dalla divisione membro a membro del medesimo sistema si ottiene:
 2  k 12
d

tan k 22   2  
2

k 22   2
 2  n 12 k 02

n 22 k 02   2
che è esattamente la formula 32 del libro.
La seguente formula 33 è data semplicemente dal rapporto:
d
2

 E y2
2
dx
0
d
2

0

E y 2 dx   E y1 dx
2
d
2
2
Far Field
Appendice al § 12.4.2 dello Sze
A partire dalla fig. 34 di pag.716 del medesimo testo, si esamina ora il cosiddetto “far field”, ossia la distribuzione di
potenza ottica entro il fascio luminoso uscente dal laser, calcolata ad una distanza z molto grande (almeno millimetri)
rispetto alle dimensioni tipiche della sezione del fascio stesso all’uscita dal chip (pochi micron).
x


z
y
Considereremo una semplice formulazione integrale del principio di Huyghens, in un sistema di riferimento come
quello in figura, con però il piano z=0 coincidente con la faccia del chip dalla quale esce la radiazione.
Sia nota su quel piano la distribuzione di campo in tutte le sue componenti. Ad esempio (come nel libro) sia nota in z=0
la distribuzione di Ey(x,y,0).
Il principio di Huyghens dice che, data una superficie radiante, ogni punto di questa superficie si comporterà come una
sorgente puntiforme, che emetterà un’onda sferica. L’effetto di questa emissione, in ogni punto x,y,z dello spazio
circostante, sarà dato dalla somma (ossia dall’integrale) di tutti i contributi di tutte le sorgenti puntiformi.
Per non fare confusione, definiamo in z=0 le coordinate x0,y0 del piano, ed indichiamo con x,y,z un punto generico
nello spazio esterno al laser. Se l’area di emissione è centrata attorno all’asse z, definiamo gli angoli in figura tramite le
relazioni sen  
x
y
e sen // 
(si noterà che questo definisce la semiapertura in entrambi i casi, per cui
z
z
l’angolo di apertura del fascio, in entrambi gli assi, sarà il doppio dell’angolo così definito).
exp ikr
, con una ampiezza pari a Ey(x0,y0,0), dove, più
r
Per ogni punto-sorgente x0,y0 si avrà un’onda sferica del tipo
esplicitamente, r è la distanza tra il punto sorgente ed il punto di osservazione:
r
x  x0 2   y  y0 2  z 2
La ampiezza della perturbazione in x,y,z, sarà quindi data da:
exp ik

E y x, y, z    E y x0 , y0 ,0
x  x0 2   y  y0 2  z 2 
 x  x0    y  y 0 
2
2
z
2
 dx dy
0
0
A grande distanza (Far Field), le dimensioni della sorgente risultano trascurabili nel denominatore, mentre
nell’esponenziale bisogna andare più cauti, facendo uno sviluppo in serie un po’ elaborato:
r
x  x0    y  y0 
2
2
2
2

x  x0    y  y0 
z
z z
2
2
2

x  x0    y  y0 
1
z2
 x  x0 2   y  y0 2 
 z 1 

2z2


x  x0 x  x0 y  y0 y  y0
x x  x0 y y  y0

z


2z
z
2
z
2
z 2
z 2
x  x0
y  y0 
x
y 1
z  sen 
 sen //
  z  sen   sen //    x0 sen   y0 sen // 
2
2
2
2 2

z
da cui si ottiene:
x
y 
 
exp ik  z  sen   sen // 
2
2 
x sen   y0 sen // dx dy

 
E y  x, y , z  
E y x0 , y0 ,0 exp  ik 0 0

 0 0
2
2
2
2

x y z
Quando si vanno a considerare le intensità, si prende il modulo quadro di questa espressione, e tutta la esponenziale
complessa esterna all’integrale scompare:
E y  x, y , z 
2
1
 2
x  y2  z2
x sen  y sen 

 E y x0 , y0 ,0exp  ik0 0  0 // dx0dy0

2

2
Questa espressione è molto prossima a quella del libro. Nel libro, si considera la sola intensità trasversale, quella
allineata lungo la direzione x, e lo si fa mettendosi nel piano zy, ossia ponendo sia y che y0 =0 (e questo rende nullo
anche sen // ) e facendo il rapporto con il valore che si ha lungo l’asse, dove sia x,y che x 0, y0 sono nulli (e quindi
sono nulli sia
sen // che sen  ) . Inoltre, il rapporto tra i moduli quadri di una componente del campo e.m. nel vuoto
equivale al rapporto tra le intensità del campo in quelle direzioni, per cui:
I  E y  x,0, z 
z2


2
I0
x2  z2
E y 0,0, z 
2
 cos2  
x sen 

 E y x0 , y0 ,0exp  ik 0 0 2  dx0dy0
 E y x0 , y0 ,0dx0dy0
x sen 

 E y x0 , y0 ,0exp  ik 0 0 2  dx0dy0
 E y x0 , y0 ,0dx0dy0
2
2

2
2
Permane qualche differenza (il segno negativo nell’esponenziale, il fattore 2 a denominatore di quello stesso esponente,
la integrazione anche nella direzione y0), ma non sono cose sostanziali. Il grafico di fig. 35 del testo è ottenuto
imponendo a primo membro il valore ½, e ponendo per il campo E y negli integrali la formula del sistema simmetrico
descritto in questa stessa dispensa nel paragrafo precedente. Con queste due definizioni, si determina implicitamente
l’angolo   .