Soluzione di Adriana Lanza
Quesito 8
In un piano riferito ad un sistema di assi cartesiani sono assegnati i punti A(0,1), B(0,4).
Si determini sul semiasse positivo delle ascisse un punto C dal quale il segmento AB è visto con un
angolo di massima ampiezza
SOLUZIONE
Si può scegliere più di una strategia risolutiva.
Considerazioni generali
a)Il punto C ha coordinate (x;0) con x>0. L’angolo B
, essendo angolo esterno del triangolo
rettangolo AOC, è necessariamente ottuso, qualunque sia la posizione di C .Nel triangolo ABC
l’angolo di vertice C è necessariamente acuto.
b)E’ possibile determinare
l’ampiezza α dell’angolo
servendosi di una delle tre funzioni
goniometriche fondamentali sen α, cos α ,tg α.
Nell’intervallo 0< α< :
massimizzare α equivale a massimizzare sen α e tg α che sono strettamente crescenti
massimizzare α equivale a minimizzare cos α che è strettamente decrescente
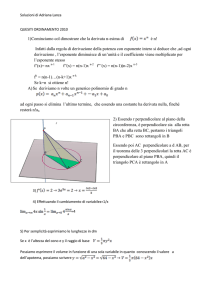
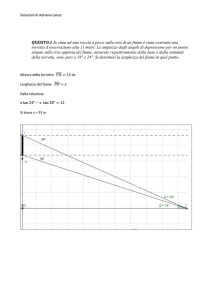
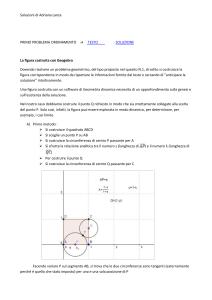
c) Una figura dinamica, costruita per esempio con Geogebra, mostra come l’ampiezza
dell’angolo
sia vicina a 0 quando C è vicino all’origine, assume un valore massimo quando
C ha ascissa 2, tende di nuovo a 0 quando C si allontana verso l’infinito
1
Soluzione di Adriana Lanza
Primo metodo
Sia
Essendo tg
= 4/x e tg =1/x sarà
Determiniamo il massimo della funzione f(x)=
nell’intervallo x>0 col metodo delle derivate,
dopo aver osservato che
La derivata prima f’(x) =
, nel suddetto intervallo si annulla per x=2 ed è positiva per 0≤x<2
f’(x) 0____________________2---------------------------------------------_
f(x)
La posizione di C per cui il valore α è
massimo è C(2;0)
In corrispondenza tg α= ¾
α= 36° 52’
2
e quindi
Soluzione di Adriana Lanza
Secondo metodo
Consideriamo la circonferenza passane per A, B e C sia r il suo raggio.
1)Dal Teorema della corda si deduce che sen α=
Sen α, e quindi α, è massimo quando r è minimo.
2)Indichiamo con p l’ascissa di C e determiniamo, in funzione di p, l’equazione della circonferenza
x2+y2+ax+by+c=0 imponendo il passaggio per i tre punti impostando il seguente sistema
Che ammette la soluzione
A questi valori corrispondono
Il centro
il valore di r =
3
=
Soluzione di Adriana Lanza
Osserviamo che al variare di p il centro G della circonferenza ha ordinata costante ( G si muove
sulla retta x=-5/2 , asse del segmento AB) quindi il raggio avrà valore minimo quando sarà minimo
il valore dell’ascissa ( G è più vicino ad A e a B)
Determiniamo il minimo richiesto studiando il segno della derivata della funzione di p
+
nell’intervallo p>0
La derivata è x’(p)=
Studio del segno
=
e si annulla per p =2
0------------------------------2____________________________
In corrispondenza del valore p=2 , pertanto, si ha la circonferenza di raggio minimo
Centro G(2;5/2) raggio r = 5/2
Sen α = →α=36 52’
La circonferenza è tangente all’asse x
Allo stesso risultato si perviene calcolando il minimo di r, ovvero di r 2, al variare di p
nell’intervallo p>0
4
Soluzione di Adriana Lanza
La derivata prima della funzione
si annulla quando p4=16 ovvero in
corrispondenza dell’unico valore accettabile p=2→ r= 5/2. In corrispondenza si ha un minimo,
come si deduce dallo studio del segno della derivata
0-----------------------------2_______________________
Terzo metodo
Determiniamo in funzione di x le lunghezze dei lati del triangolo ABC
Dal Teorema di Carnot
cos α
È possibile determinare cos α=
La derivata prima
Nell’intervallo x>0, è negativa per x<2 e positiva per x>2
Studio del segno
Per x=2
5
0------------------------------2____________________________
cos α assume valore minimo e α assume valore massimo